A kérdés megválaszolása ismét a statisztika eszközeiért kiált. Mint az élet egyéb alapvető kérdései általában, ez a kérdés sem újkeletű. „Isaac Newton és Christiaan Huygens már a XVII. században parázs vitát folytatott erről, amikor Newton a Principia Mathematica című művét írta. Newton úgy vélte, hogy egy tárgy folyadékban való haladásának sebessége függ a folyadék viszkozitásától, míg Huygens szerint ez a tényező nem lényeges. Mivel nem tudtak megegyezni, Newton mindkét verziót beleírta könyvébe.”
/Forrás: Szörpben is lehet gyorsan úszni – National Geographic, Fehér Hajnalka, 2010 október 4/
Mint eldöntetlen kérdések esetében ez szokásos, a téma sokak fantáziáját megmozgatta a komoly tudósoktól a médiasztárokig. A téma eddigi legismertebb feldolgozását a Mítosz rombolók (Mythbusters) című sorozat egyik részében Adam Savage és Jamie Hyneman Nathan Adrian olimpiai bajnok úszó segítségével próbálta gyakorlatban is kipróbálni, vajon van-e különbség a kétféle sűrűségű folyadékban való úszás sebessége között. A témában tudományos kutatás is született, amely 2005-ben elnyerte a kémiai nobel-díjat a rangos IG Nobel versenyen (�).
/Referencia: “Will Humans Swim Faster or Slower in Syrup?” American Institute of Chemical Engineers Journal, Brian Gettelfinger and E. L. Cussler, vol. 50, no. 11, October 2004, pp. 2646-7. - https://www.improbable.com/ig-about/winners/#ig2005/
A fent említett tudományos elemzésben 20 úszó próbált meg tiszta, illetve guargumival besűrített vízben úszni. A kísérlet során gondosan rögzítették a sportolók teljesítményét és azt vizsgálták, hogy a sűrűbb közegnek van-e érzékelhető hatása az úszók sebességére. A kísérletsorozat a következő eredményeket hozta:
/Forrás: A táblázatban szereplő adatok már első ránézésre is azt mutatják, hogy nincs jelentős eltérés az úszóknak a kétféle közegben elért sebessége között. A kérdés viszont ez esetben nem ez, hanem hogy van-e lényeges különbség a kétféle közegben való úszás esetében az egyes úszók sebessége között. Előfordulhat, hogy a vízben a sportolók egyenletesebb teljesítményt nyújtanak vízben, mint a sűrűbb szirupban. Mondjuk én jobban örültem volna, ha az időeredményeket tudom elemezni, mert az pontosabb lenne. Legalábbis úgy érzem, hogy a sebességeket minimum több tizedesjegyig illett volna megadni, mert ez végül is egy számított érték, vagyis torzíthat. Erre persze nincs bizonyítékom, de kizárni sem tudom. Sajnos az időeredményeket nem találtam meg sehol, szóval szegény ember vízzel főz…
A varianciák összehasonlításának egyik elterjedt módja az úgynevezett Levene’s test. Ez a teszt egy elsőre bonyolultnak tűnő képletet alkalmaz a próbastatisztika kiszámítására. A teszt előnye, hogy nemcsak kettő, de három, négy vagy akárhány adatminta varianciáját is össze tudja hasonlítani. A próba statisztika képlete a következőképpen néz ki:
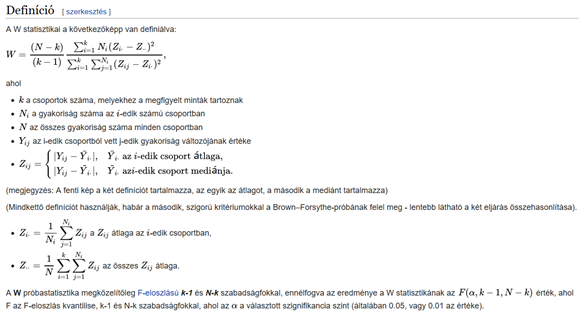
/Forrás: Wikipédia - https://hu.wikipedia.org/wiki/Levene-próba/
Ehhez most szívesen vásárolnék egy-két betűt, mert azért nem tűnik túl egyszerűnek, pedig a négy alapműveleten meg négyzetre emelésen kívül nem sok más titok van benne. De azért megpróbálom visszafejteni a kódot.
Az az érdekes, hogy ezt a bejegyzést egy kicsit össze-vissza kell olvasni. A történet a fenti idézet közepén kezdődik a Zij változó definíciójánál. Mi is az a Zij?
Először is tisztázzuk, hogy van 2 darab adatsorunk, amelyet össze akarunk hasonlítani. Az egyik a vízben, a másik pedig a szirupban mért sebességeket jellemzi. Ezt jelöljük k-val, azaz ebben az esetben k = 2.
Mindkét adatsorban van 20 darab érték, amelyet most jelöljünk N-nel, tehát N = 20.
A fenti szöveg azt mondja, hogy legelőször is definiál egy Zij változót, amely a fentiek szerint az Yij - Y̅ különbség abszolút értéke. Jé, ez ismerős! Ez tulajdonképpen az i-dik adatsor j-dik elemének távolsága az i-dik adatsor átlagától! Erről esett szó egy korábbi bejegyzésben (Variancia négyzetgyöke vs. eltérések abszolút értéke), ott ezt a számítási módot „eltérések abszolút értéke”-ként aposztrofáltam. Ez így néz ki grafikusan a fenti példa esetében:
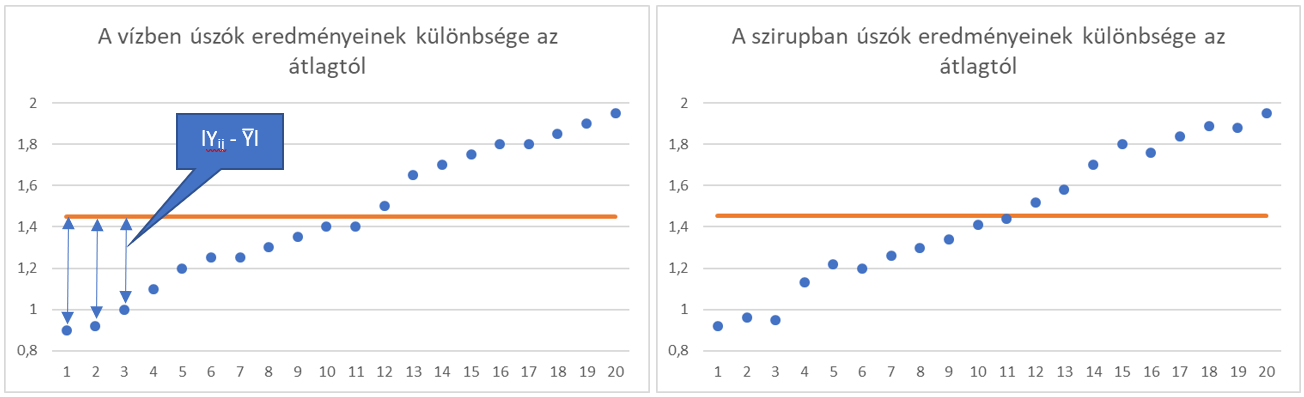
Akkor most vegyük a Zi. változót. A Zi. változó tulajdonképpen összeadja az i-dik adatsor összes elemének távolságát az i-dik adatsor átlagától és elosztja azt az i-dik adatsor elemeinek számával, azaz veszi az i-dik adatsor pontjainak ÁTLAGOS eltérését az i-dik adatsor átlagától. Ha jól érzékelem, ez MAJDNEM az adatsor szórása, csak nem a négyzetreemelős-gyökötvonós, hanem az abszolútértékes változat!
Jaj de remek, vajon miért kell ezt ilyen kacifántosan jelölni?
És akkor jöjjön az utolsó rejtélyes változó, a Z.. Ez pedig a k számú adatsorban szereplő összes adatpont távolsága annak az adatsornak az átlagától, amelyikhez az adott adatpont tartozik! A vizes-szirupos példában ezek a következőképpen néznek ki:
A B5:D25 tartomány tartalmazza a kiinduló adatokat. A C2 és D2 mezőkben vannak az eredeti adatsorok átlagai.
A G5:G25 tartományban számoltam ki a vizes adatsor esetében a j-dik adatpont távolságát az átlagtól.
A K5:K25 adatsorban hasonlóan számoltam ki az átlagtól való eltéréseket a szirupos adatsor esetében. A H és az L oszlopokban kiszámoltam a különbségek abszolút értékét mindkét adatsorra. Végül kiszámoltam Zi. értékeit mindkét adatsorra (H27 és L27 mezők), illetve Z.. értékét is a H29 mezőben.
Hogy is van ennek az egésznek a felépítése? A hierarchia minden szintjén a következő feljebbi szint átlagától való eltérést vizsgálgatjuk, ezeket hasonlítgatjuk egymáshoz a különféle adatsorok esetében.
Most már csak a W próba statisztika értelmezése maradt hátra. Kezdjük a képletben szereplő második törttel.
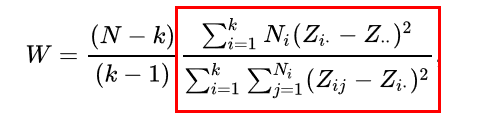
A számlálóban szereplő képlet azt mondja, hogy számoljuk ki a Zi. és a Z.. változók különbségét mindkét adatsorra, ezeket emeljük négyzetre, majd a négyzetre emelt különbségeket szorozzuk meg az adatsorokban szereplő adatok darabszámával, majd ezeket adjuk össze mind a k adatsor esetében. Aha, itt most vesszük az egyes adatsorok átlagos szórásait és megnézzük ezek távolságát a k darab adatsor szórásainak átlagától.
A nevező egy szinttel lejjebb végzi el ugyanezt, hiszen ott az egyes adatsorok összes elemének távolságát veszi az adott adatsor átlagától és ezeket összegzi:
Rendben, de mit jelent, ha a tört értéke nagy, illetve, ha a tört értéke kicsi? Ha a számláló értéke kicsi, az azt mondja, hogy az egyes adathalmazok átlagos eltérései közel vannak a k darab adatsor összes elemének átlagos eltéréseihez, vagyis az adatsorok átlagos eltérései nincsenek messze egymástól. Ha a számláló értéke nagy, akkor viszont egy vagy több adatsor átlagos eltérése kilóg a sorból, mert ezek messzebb vannak az összes adatsor összes adatának átlagos eltérésétől!
A tört nevezőjét hasonlóképpen lehet értelmezni. A nevező értéke akkor lesz nagy (azaz a tört értéke akkor lesz kicsi), ha az adatsorokon belüli szórások nagyok, és akkor lesz a nevező értéke kicsi (azaz a tört értéke nagy), ha az adatsorokon belüli szórások kicsik.
Tehát a tört értéke akkor lesz nagy, ha az adatsorokon belüli szórások kicsik, de az adatsorok közötti szóráskülönbségek nagyok. Ezzel szemben a tört értéke akkor lesz kicsi, ha az adatsorokon belüli szórások nagyok, de az adatsorok közötti szórások kicsik. Vagyis, ha a tört értéke nagy, akkor van eltérés a vizsgált adatsorok varianciája között, ha a tört értéke kicsi, akkor pedig nincs.
Mi jött ki a mi esetünkben?
A tört számlálója a következő:
A tört nevezőjének kiszámításához soronként négyzetre kell emelni a Víz és a Szirup oszlopokban szereplő értékeket, azaz az egyes adatpontok átlagtól való eltéréseit, …
… majd mindezeket össze kell adni. Ezt most nem szeretném itt kifejteni, kiszámoltam táblázatkezelőben és Wnevező = 4,28543-at kaptam.
Ha megvan a számláló és a nevező, akkor ezeket el kell osztani egymással és megkapjuk a W próba statisztika második törtjének az értékét:
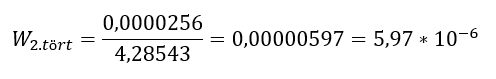A W próbastatisztika első törtjéről még nem ejtettem szót. Konkrétabban az
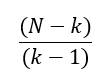
törtről beszélek. Ebben csak az adatsorok száma (k) és az összes adatpont száma (N) szerepel, valószínűleg ez egy korrekciós tényező, amely az adatsorok és az ezeken belüli adatpontok száma alapján korrigálja a próbastatisztika értékét. Mivel két adatsorunk van, ezért k = 2, és a két adatsorban összesen 40 darab adatpont szerepel, ezért N = 40. Így a fenti tört értéke
Most már az összes részadat a rendelkezésünkre áll W kiszámításához:
Ezek szerint W értéke egészen kicsi. De mennyi a határérték, amivel a próba statisztikát össze kell hasonlítani? Mivel W értéke egy olyan F-eloszlást követ, amelynek a két paramétere k-1 és N-k, ezért újra fel kell csapnunk az eloszlás táblázatot és ki kell keresnünk mekkora F-érték tartozik a 95%-os megbízhatósági határértékhez k-1 = 1 és N-k = 38 esetén:
A táblázatban sajnos nincs benne a 38-hoz, csak a 40-hez tartozó határérték. Mivel az így kapott 5.42 és a W próba statisztika, azaz 0,000227 között hatalmas a különbség, ezért nem követünk el nagy hibát azzal, ha ezt az értéket használom. Az így kapott eredmény azt mutatja, hogy a két adatsor varianciája között nincs szignifikáns eltérés, azaz az úszók körülbelül ugyanolyan kis szóródással tudnak úszni mind a vízben, mind pedig a szirupban.
Így néz ki az egész táblázatkezelőben:
Összegzés:
Az általunk levezetett teszt igazolta azt, amit korábban már feltételeztünk, azaz meglepetésre az úszók ugyanolyan sebességgel tudnak úszni vízben és sűrű szirupban is. Egy következő cikkben – szokásomhoz híven – bemutatom majd azt is, hogy hogyan kell ezt a tesztet Minitab segítségével megoldani.
