
A témához kapcsolódó előző cikkben (Használtautó eladó! – Többváltozós lineáris regresszió elemzés) bemutattam az alap problémát, amelyet meg akarunk oldani. Most megpróbálom veled együtt megtenni a következő lépést, azaz belemerülni abba, hogy mit is jelent a többváltozós lineáris regresszió.
Az előző bejegyzésben említett példa persze akár még jó is lehet, de nem arra, hogy megértsük az elemzés működését. Vagyis kell egy olyan adatsor, ami sokkal rövidebb a használtautósnál, hogy a számolások egyszerűen követhetők legyenek. Ezért létrehoztam egy 3 oszlopból és 5 sorból álló kis táblázatot, amely tartalmaz egy x1 és egy x2 oszlopot. Ezek lesznek a független változók, amelyek meghatározzák majd a harmadik oszlopban szereplő y függő változó értékét. A kiinduló táblázatunk így néz ki:

Már korábban is többször említettem, hogy nagyon fontos a számomra, hogy elhiggyem, hogy egy adott teszt vagy elemzés működik. Ez most sem lesz másképpen, ezért természetesen kihívásként fogom kezelni ezt a kis levezetést, azaz a harmadik oszlopban szereplő értékeket ténylegesen az első két oszlopban szereplő számok alapján határoztam meg. Meg is adom itt azt az egyenletet, amelyet erre használtam:
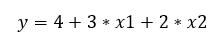
Ez most arra lesz jó, hogy vissza tudjuk ellenőrizni a számítás helyességét. Ha a végén kijön ugyanez (vagy kb. ugyanez) az egyenlet, akkor nyugodtan elhihetjük, hogy bármennyire hihetetlenül is hangzik, a dolog működik és megbízhatunk benne. A bizalom erősítése érdekében végig is számoltam mind az öt sort:
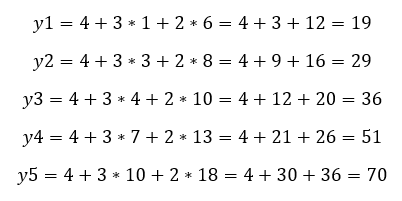
Ez eddig megvan. Most viszont azt kellene tisztáznunk, hogy tulajdonképpen mit is jelent a fent említett egyenlet? Hogyan képzeljük el? Az y=ax+b egyenletet elég könnyen el tudtuk képzelni magunk előtt, hiszen van egy x és egy y változónk, az egyiket a vízszintes, a másikat a függőleges tengelyen ábrázoljuk. Igen, de most két x változónk van, x1 és x2? Hogy néz ki ez az egyenes? Egyáltalán egyenes lesz, vagy inkább egy sík? Hogyan ábrázoljuk a pontokat? Szerencsére itt még egyszerű dolgunk van, mert ugye a kétféle x-változó és az y változó együtt háromféle koordináta tengelyt igényel és ezt még tudjuk ábrázolni. Nos a fenti öt pont ebben az esetben valahogy így néz majd ki:
Azért készítettem animációt, mert úgy éreztem, hogy így tudom a legjobban bemutatni a pontok és a rájuk fektetett egyenes vizuális megjelenését. Vagyis a pontok a háromdimenziós térben lebegnek, az egyenes pedig ugyanezen a háromdimenziós téren fut keresztül. Vagyis a korábbi kétdimenziós grafikonunkhoz hozzáadtunk egy harmadik dimenziót is. Viszont, ha már hozzá tudtunk csapni egy plusz változót, vagyis egy plusz befolyásoló tényezőt az egyenletünkhöz, akkor mi akadályoz meg bennünket abban, hogy akár még egyet hozzáadjunk, azaz legyen egy x3 oszlopunk is? Eme cselekedetünk társadalmi hasznosságát nehéz lenne kétségbe vonni, de a fent ismertetett ábrázolásmód és gondolkodás sajnos erősen korlátoz bennünket abban, hogy ezt tovább is merjük gondolni, hiszen azt az egyenletet már elég macerásan tudnánk ábrázolni, hiszen a térnek jelenleg csak három dimenzióját tudjuk értelmezhetően megjeleníteni (ha az időt nem tekintjük negyedik dimenziónak). Ha viszont eltekintünk az adatok vizuális megjelenítésétől, akkor egyszerre csak kinyílik előttünk a világ, hiszen a számok nyelvén ’akárhány-dimenziós’ egyenlettel is le tudjuk írni az y függő változót befolyásoló tényezők együttes hatását, azaz az y-t bemutató egyenes függvényképletét.
De ha ennyire rugalmasak akarunk lenni, azaz egy olyan eszközt akarunk létrehozni, amelyet az adathalmazoknak egy igen széles skáláján szeretnénk használni, függetlenül attól, hogy az adathalmaz hány sorból áll, illetve az y függő változónkat hány x1, x2, …, xn független változó befolyásolja, akkor szükségünk van az adatoknak egy olyan ábrázolási módjára, amely
elég rugalmas ahhoz, hogy az adatsoroknak ezt a rugalmas változékonyságát le lehessen vele kezelni,
az adatokat rendezetten lehessen bennük kezelni, azaz kicsi legyen a tévesztés lehetősége, és
kialakult matematikai formulákkal lehessen kezelni az így ábrázolt adatokat.
És létezik ilyen módszer, ezek a mátrixok. Egy mátrix igazából szinte bármekkora méretű, dimenziójú és alakú lehet. Az adatok a mátrixokban rendezett formában helyezkednek el, minden adatnak megvan a maga helye, illetve a mátrixokkal, illetve mátrixok között elvégezhető műveleteknek széles körét ismerjük. Nézzük meg, hogyan is néz ki ez egy kicsit általánosabban. Ha feltételezzük, hogy van egy olyan adatsorunk, ahol y értékét az x1, x2, … , xm tényezők befolyásolhatják, és van y1, y2, … ,yn darab függő változónk a vizsgált sokaságból, akkor a keresett függvény képlete a következőképpen néz ki:
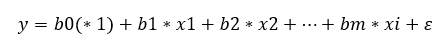
Mi b0, b1 és bm? Ezeket akarjuk kiszámítani a most következő levezetéssel. Az egyváltozós regresszió elemzéskor a b0-t a-nak, a b1-et b-nek neveztük (Tudom, hogy gőzgép, de mi hajtja? – Egyváltozós lineáris regresszió – a regressziós egyenes meghatározása). Az a picike kis görög betű a képlet végén jelöli az egyenlet hibáját, hiszen az egyenlet meghatározásához használt x-értékek a minták értékei. Vagyis itt is igaz az a bölcsesség, amelyet már korábban is megállapítottunk, hogy a minták alapján kiszámított/becsült ŷ érték nem fog pontosan megegyezni a sokaság y̅ átlagértékével, csak közelíti azt. A fenti egyenlet alkalmazásával ki tudjuk számítani a minták (azaz a mátrixok sorainak) y értékeit. Például az adathalmazunk első sorát így számítanánk ki:

ahol x11 a kiinduló adathalmazunk első sorában az x1-hez tartozó érték, x21 az első sor x2-höz tartozó értéke, y1 pedig az első sor y-hoz tartozó értéke.
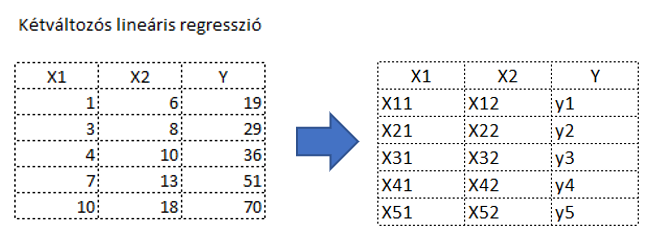
Ez ugyanaz, mint amit a cikk elején tettünk, kiszámoltuk az egyes sorok esetében az x1 és x2 értékekhez tartozó y értékeket, vagyis
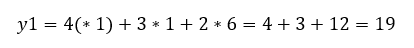
Itt válik érthetővé a fentebb a b0 után zárójelben szereplő *1, hiszen az x1 … xm értékeit tartalmazó mátrixban a b0 konstanshoz tartozó 1-eket is szerepeltetnünk kell. A fenti példa esetében ez a mátrix így néz ki (most már szerintem te is látod, hogy miért választottam egy jóval egyszerűbb adatsort az elmélet bemutatásához):
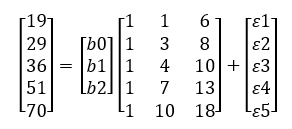
Azért, hogy a későbbiekben bizonyos dolgokat egyszerűbben tudjak elmagyarázni, nevezzük el a fenti vektorokat és mátrixokat egy-egy betűvel.
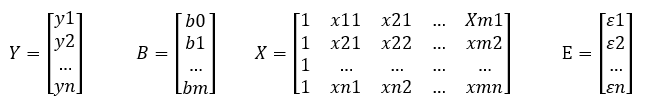
Akkor most írjuk fel a fenti egyenletünket a most definiált betűk segítségével:
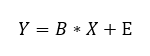
Ez így sokkal barátságosabban néz ki, csak ne felejtsük el, hogy minden betű egy mátrixot vagy egy vektort reprezentál.
Tehát a célunk az, hogy meghatározzuk b0, b1 és b2 értékeit úgy, hogy az ε1...εn hibák értéke minimális legyen. Ahhoz, hogy az életünk így az elején egy kicsit egyszerűbb legyen, tételezzük fel, hogy a leendő képlet tökéletes eredményt fog adni, vagyis ε1, ε2, ... , εn értéke mind 0. Így az egyenletünk a következő marad:
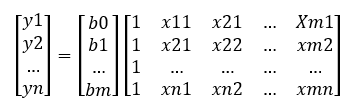 vagyis
vagyis 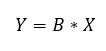
Hurrá, így már csak a B vektor értékei maradtak ismeretlenek a számunkra, amelyeket így már könnyedén kifejezhetünk a fenti egyenletből!
Nagyobbat nem is tévedhettünk volna…
Sajnos a mátrixokkal nem úgy tudunk műveleteket végezni, mint az egyedi számokkal, így itt egy kis további számolási gyakorlatra van szükségünk. Először is tisztáznunk kell, hogy mit jelent egy mátrix transzponálása. Hú, ez most nagyon kínaiul hangzik, pedig nem ördöngősség, a transzponálás során egészen egyszerűen felcseréljük egy mátrix sorait az oszlopaival. A kis példánkon bemutatva a dolgot, az X mátrixot transzponálva a következőt kapjuk:
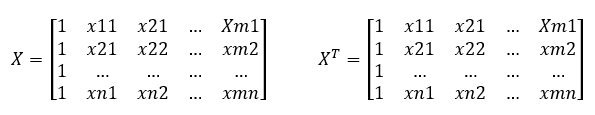
avagy
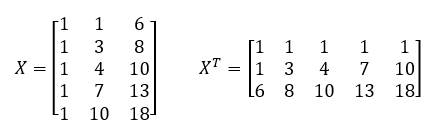
Ez még eddig nem volt varázslat, az most jön (annak ellenére, hogy csak összeadás és szorzás van benne…). Most, hogy ilyen ügyesen transzponáltuk az X mátrixot, most képezzük az X és az XT mátrixok skaláris szorzatát!
STOP!
Mit jelent a mátrixok skaláris szorzata? Ezt megpróbáltam szabatosan leírni, de folyamatosan csak valami zavaros és érthetetlen zagyvalék jött ki belőle, úgyhogy úgy döntöttem, inkább bemutatom a fenti példán:
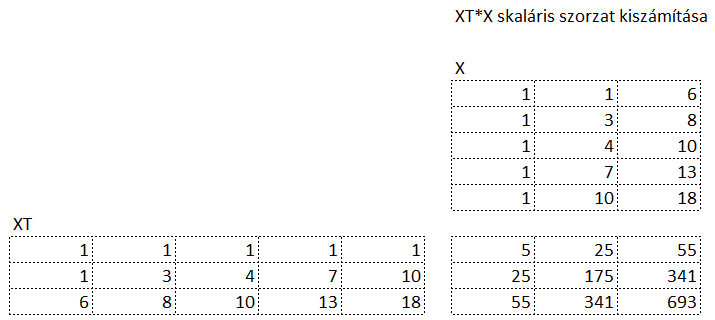
Fent látható az X mátrix, bal oldalon pedig az XT, azaz a transzponált mátrix. Középen pedig a skalár szorzat eredményeként kapott mátrix található. Kezdjük az eredmény mátrix bal felső cellájával. A bal felső cellában az X mátrix első oszlopának és az XT mátrix első sorának szorzatösszege található. Az eredményként kapott 5 a következő módon jött ki:
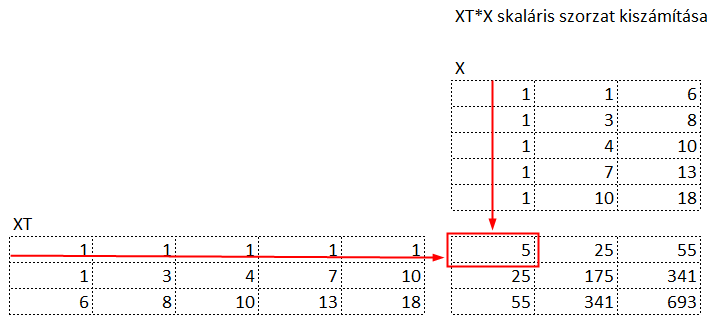
azaz
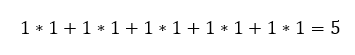
Vagyis az X mátrix első oszlopának első elemét össze kell szorozni az XT mátrix első sorának első elemével, majd ehhez hozzá kell adni az X mátrix első oszlopának második elemének és az X mátrix első sorának második elemének szorzatát, és így tovább ötig. Az eredmény mátrix első sorának második cellájában található eredmény hasonlóképpen jött ki, csak az XT mátrix első sorát az X mátrix második oszlopával kell összeszorozni,
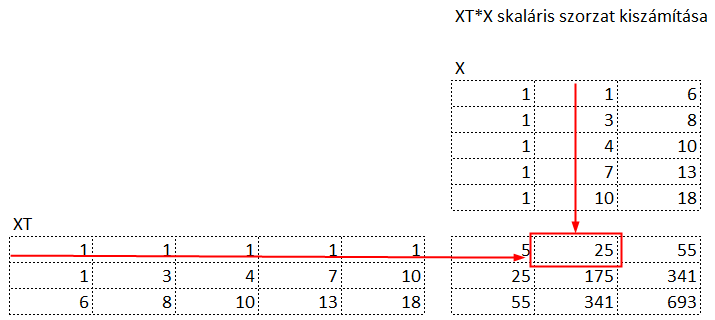
azaz
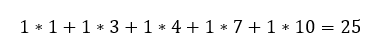
Az eredmény mátrix közepén lévő 175 szintén ily módon adódott.
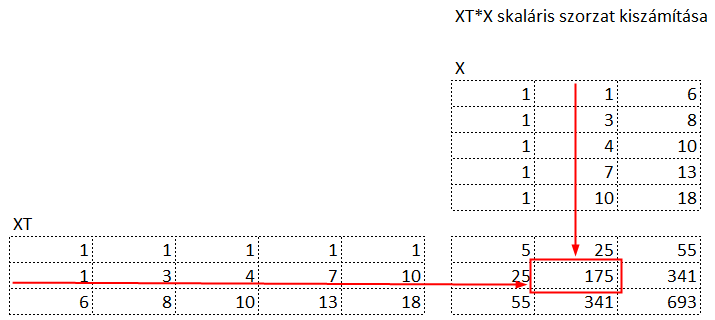
vagyis
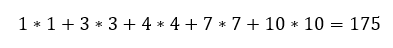
Ha van kedved, nyugodtan számold végig kézzel vagy táblázatkezelő segítségével, de remélem ennyi magyarázat elég a skaláris szorzat lényegének megértéséhez.
Jó, de miért hajtottuk végre ezt a csodálatos varázslatot? Azért, mert az így kapott eredmény mátrix egy úgynevezett variancia-kovariancia mátrix, amelynek átlójában tulajdonképpen az X mátrix oszlopait önmagukkal szorozzuk be, vagyis az X mátrix egyes sorainak négyzetösszegeit kapjuk meg. Ezek lesznek az X értékek varianciáinak n-szeresei (hiszen ezeket nem osztottuk el n-nel). És mik is vannak az X mátrix oszlopaiban? 1, x1 és x2, amelyeket majd b0-al, b1-el és b2-vel fogunk megszorozni a keresett egyenletben.
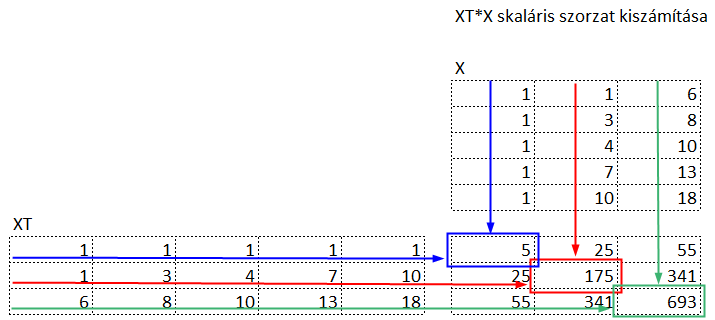
Az eredmény mátrix többi cellájában 1, x1 és x2 különböző kombinációinak szorzatösszegei találhatók, amelyek számunkra sajnos érdektelenek lesznek, vagyis ezeket majd ki kell szűrnünk valahogy.
És ehhez a kiszűréshez ismét egy új - mátrixokkal kapcsolatos - fogalmat kell megismernünk, ez pedig az egységmátrix fogalma. az egységmátrix egy olyan egyenlő oldalú, azaz négyzetes mátrix, amelynek a bel felső saroktól a jobb alsó sarokig húzódó átlaga 1, a többi mezőben pedig 0 található. Természetesen egy egységmátrix bármilyen méretű is lehet, de az egyszerűség kedvéért; illetve azért, mert a példánkban is egy háromszor hármas mátrix szerepel, ezért az ide biggyesztett egységmátrix is 3x3 méretű:
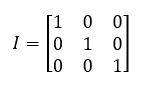
Jé, ez az ábra eléggé hasonlít az előző variancia-kovariancia mátrixhoz és érdekes módon pont azok a cellák 1-ek, ahol a minket érdeklő varianciák vannak, illetve ott nullák, ahol a minket nem érdeklő kovarianciák. Nahát, nahát…
És van még egy számunkra érdekes törvényszerűség. Minden négyzetes mátrixnak van egy olyan mátrix párja, amelyet, ha skalárisan összeszorzunk önmagával, akkor egy egységmátrixot kapunk! Hogy bemutassam, hogy ez mit jelent, létrehoztam a mi kis eredmény mátrixunknak is ezt a párját:

A fenti mátrix az előbb megkapott eredmény mátrix, a bal oldali pedig az eredmény mátrix inverze (az inverzet a -1 hatvánnyal jelöljük, ami nem azt jelenti sajnos, hogy a mátrixot egyszerűen a tört nevezőjébe tesszük). Középen látható a két mátrix skaláris szorzataként kapott mátrix, amely egy egységmátrix. Csak példaképpen nézzünk bele két-három skaláris szorzatba. Például a bal felső cella értéke a következő módon adódik:

vagyis
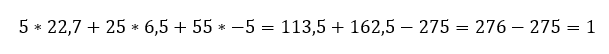
Nézzük meg mondjuk a bal oldali oszlop legfelső celláját:

azaz
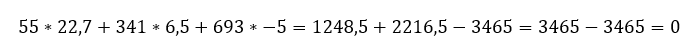
Úgy tűnik, hogy működik a rendszer, ezt is végig lehet számolni, ha van kedved. Szerencsére a táblázatkezelő ebben ritkán téved.
Miután sikerült teljesen összezavarni ezekkel a mátrixos varázslatokkal, végre leírom ide azt, hogy miért is volt szükség erre a sok különféle mátrix műveletre. Ott tartottunk a kitérő előtt, hogy
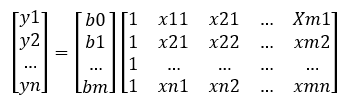
vagyis
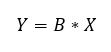
és ugye ki kellene varázsolni a B vektort az egyenletből. Először is szorozzuk meg az egyenlet mindkét oldalát XT-vel.
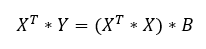
Jól felismerhető a zárójelben az első lépésként elvégzett skaláris szorzás az X mátrix transzponáltja és az X mátrix között. Most pedig szorozzuk meg az egyenlet mindkét oldalát az (XT*X) mátrix inverzével!
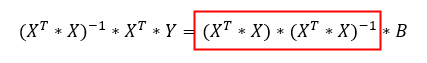
Éééééés TAPS!
Mivel
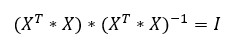
azaz a B vektor előtt álló skaláris szorzat éppen megegyezik az egység mátrix-szal – amelynek az átlóiban 1 van, a többi helyen nulla, ezért az egyenlet jobb oldalán a B vektor összes elemét megszoroztuk 1-gyel, vagyis a jobb oldalon a B vektor áll önmaga csupasz valójában, „csak” az egyenlet bal oldalán álló szerény kis mátrix műveletet kell elvégeznünk b0, b1, és a többiek értékének kiszámításához!
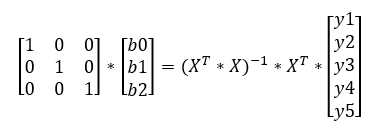
Az Y vektor előtti bonyolult kifejezés kétharmada már készen van, már csak skalárisan meg kell szorozni XT-val, majd az úgy kapott mátrix-szal meg kell szorozni az Y vektort és már meg is vagyunk. Természetesen ezeket is elvégeztem:
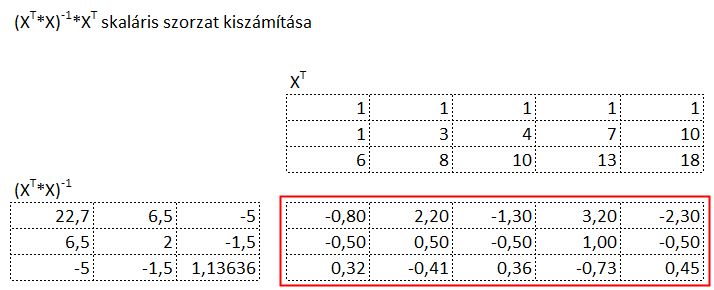
Majd a zölddel bekarikázott mátrix-szal megszorzom az Y vektort:
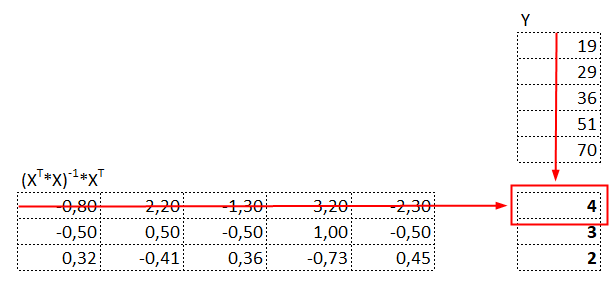
azaz
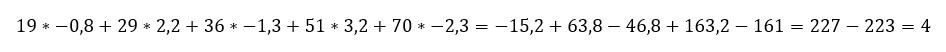
illetve
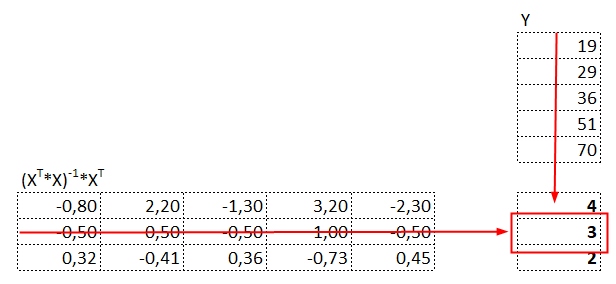
azaz
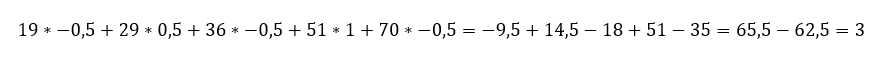
és végül

vagyis
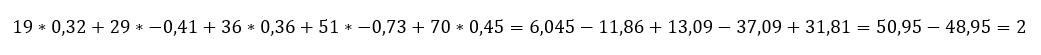
Vagyis kijött a végére ugyanaz az egyenlet, ami alapján az elején kiszámoltam y értékét x1 és x2 függvényében:
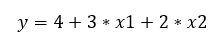
Hát ez elég meredek volt és nem csodálkozom, ha kimerültél a végére, kedves olvasó. Nagyon remélem, hogy eljutottál idáig és többé kevésbé sikerült is megértened a módszer lényegét úgy tizedik olvasásra. A lényeg tehát tömören annyi, hogy az egyenlet egyes tényezőit mátrix műveletek segítségével lehet kiszámítani és sajnos ezeknek nem sok köze van a keresett egyenes vizuális megjelenéséhez, inkább csak bűvészkedés a számokkal, hogy egy vektorokból és egy mátrixból álló egyenletből valahogy ki lehessen varázsolni a B mátrix egyes tagjainak értékét. Mindezzel együtt a projekt sikerrel járt és visszakaptam az eredeti egyenletet, így hiába a sok varázslat, végül is el kell ismernem, hogy működik a dolog.
A következő bejegyzésben megpróbálom ugyanezt a táblázatkezelős varázslatot a használtautós adattáblámra is alkalmazni, ami egy újabb kihívás lesz a dolog nagyobb számítási igénye miatt. Nem tudom, hogy ezt valaha valaki is elvégezte volna egy ekkora adattáblán, de az biztos, hogy nekem ez lesz a saját különbejáratú Guiness-rekordom a magam számára. Legalábbis ebben a pillanatban…





