A lineáris regresszió valahogy mindig is mumus volt a számomra. Tudom, hogy mire való, lehet is vele játszadozni, de igazából sohasem értettem, hogy mitől működik az a bonyolult képlet, amit az egyenes meredekségének kiszámítására alkalmaznak (vagy legalábbis, amit a legtöbb statisztika könyvben vagy weboldalon meg lehet találni). Erről a képletről valahogy mindig az jut az eszembe, hogy összehányt x-ek és y-ok valahogyan összedobált halmaza.

Ugye szép?

Vagy ez sem rossz a wikipédiáról (Az különösen tetszik, hogy a betűket megvédjük az esőtől):

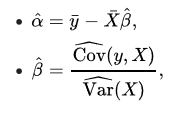
Biztos működik, de sosem próbáltam ki, noha még levezetett példákat is lehet találni a neten, amiken csak végig kellene baktatni egyesével képletről - képletre. De kinek van ehhez kedve?

De mégis mitől működik ez az egész? Miért pont ez a képlete a-nak és b-nek az y = ax + b egyenes függvény egyenletében? Szóval lassan hetek óta keresgélem, hogy mi is ez az egész lineáris regresszió és aki kitalálta, az miért pont ezt a csodát találta ki. Igazából lassan, lépésről - lépésre sikerült összerakni a mozaik darabkáit és kitalálni egy olyan szisztémát, amelynek segítségével egy kicsit érthetőbben el tudom mondani a történetet. Ebben persze csak reménykedem, mint ahogy abban is, hogy te is megérted azt, amit én.

Tehát ott tartottunk (Legyenek a négyzetek minél kisebbek…! – útban a lineáris regresszió elemzés felé), hogy vannak pontjaink, amikre egy egyenes vonalat szeretnénk ráfektetni úgy, hogy az minél inkább passzoljon a pontokhoz. Ennek az egyenesnek szeretnénk meghatározni az y = ax + b függvény esetében a és b értékét, amelynek segítségével ezt ténylegesen fel tudjuk rajzolni az egyenest egy grafikonra, illetve hogy a függvény képletébe x értékét behelyettesítve ki tudjuk számolni, hogy az általunk kiválasztott x értékhez milyen y érték tartozik. Abban is megegyeztünk, hogy egyetlen olyan egyenes van, amelynél a pontok és az egyenes y-irányú távolságaira rajzolt négyzetek területe minimális. Most ezt a bizonyos egyenest keressük.

Nos, az internet néhány rejtett zugában a értékére egy másik képletet is lehet találni, amely így néz ki:

ahol rxy a korábbról már jól ismert korrelációs együttható (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?), sy és sx pedig a pontok x és y koordinátáinak szórása, azaz eltérése az x és az y koordináták átlagától, vagyis

De hogyan néz ez ki vizuálisan? Az előző cikkben már szerepelt ez a grafikon, de most berajzoltam az x és az y változók átlagát, illetve látható a jobbszélső pont távolsága az x és az y átlagtól. Ez az ábrázolás már ismerős lehet a korrelációs együtthatóról szóló cikkből is (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?).

Ha ezeket a távolságokat négyzetre emeljük, az ugyanaz, mintha mindegyik ponthoz rajzolnánk egy olyan négyzetet, amelynek az oldalhosszúsága megegyezik a pont átlagtól mért távolságával.

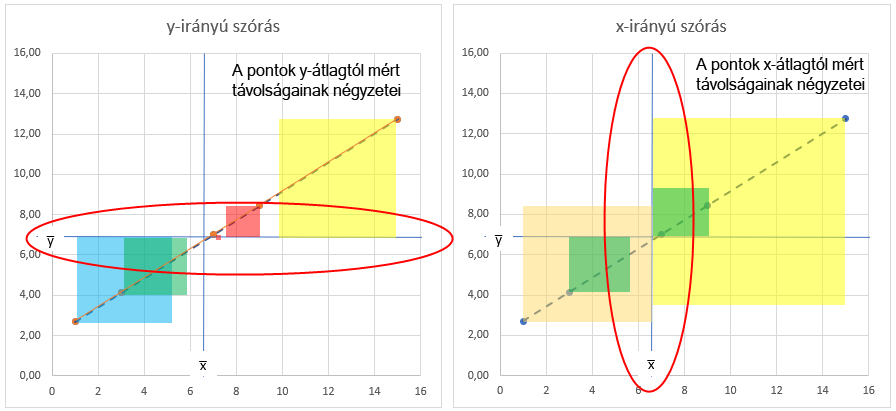
Sy és Sx úgy jön ki, ha ezeknek a négyzeteknek összeadjuk a területét, majd elosztjuk a négyzetek számával, így megkapjuk az összes ponthoz tartozó négyzetek átlagát. És ezen a ponton egy érdekes dolgot figyeltem meg. A pontok által kijelölt egyenes általában keresztül megy az x̅ és az y̅ metszéspontján. Ha az egyenes meredeksége kisebb, akkor a pontok y̅-tól mért távolsága, és ezáltal a pontokhoz rajzolt négyzetek területe lényegesen kisebb, mint az x̅-hoz rajzolt négyzeteké.

Ezzel szemben, amikor az egyenes meredeksége nagy, akkor pont fordított az eset. Az y̅-hoz rajzolt négyzetek területe nagy és az x̅-hoz rajzolt négyzetek területe kicsi.

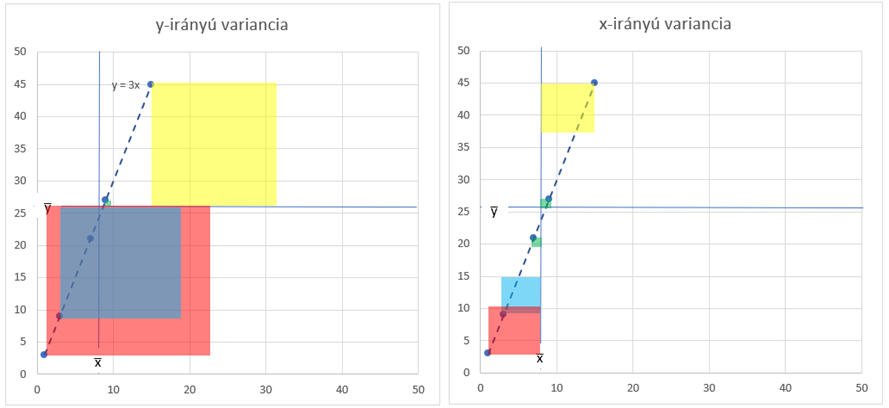
Vagyis fennáll egy arányosság a keresett egyenes meredeksége és az x̅-hoz, illetve az y̅-hoz rajzolt négyzetek mérete között. Tulajdonképpen a két átlaghoz rajzolt négyzetek területének aránya megadja az egyenes meredekségét, hiszen amikor Sy-t elosztjuk Sx-el, akkor mindkét szórás esetében elosztjuk a négyzetek összterületét a pontok számával, ezért az arány ettől nem változik. De ne változtassunk a hivatalos állásponton, vagyis az Sy és az Sx szórások hányadosa megadja a pontokra illeszthető egyenes meredekségét. DE VIGYÁZAT!

Ez csak akkor igaz, ha a pontok egyébként TÖKÉLETESEN illeszkednek az egyenesre, azaz az előző bejegyzésben tárgyalt Σ(yi-ŷ)² = 0, azaz a korrelációs együttható értéke 1! De mi történik akkor, ha a pontok nem tökéletesen illeszkednek az egyenesre? Ilyenkor az Sy és az Sx hányadosa által megadott meredekségű egyenes elkezd fokozatosan felfelé húzni, azaz egyre inkább elhagyja a pontok által kijelölt terület közepét és ezzel párhuzamosan egyre távolabb metszi az x̅ és az y̅ vonalait azok metszéspontjától.

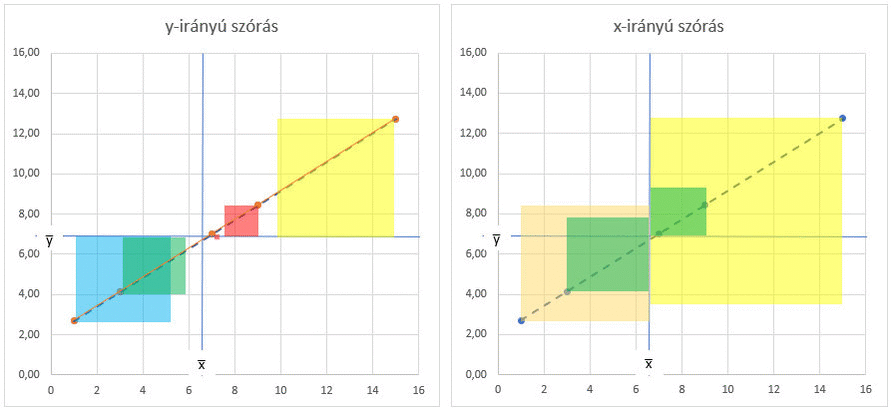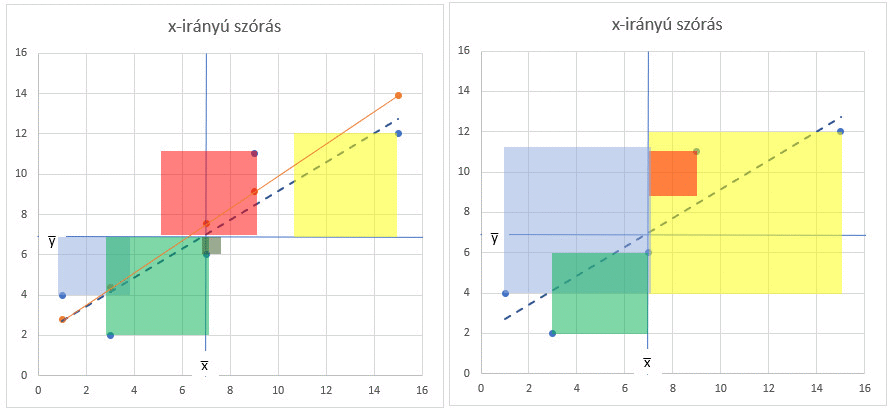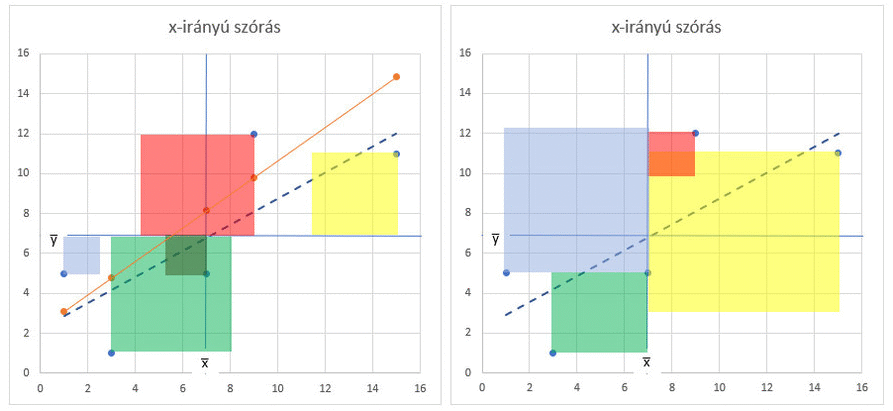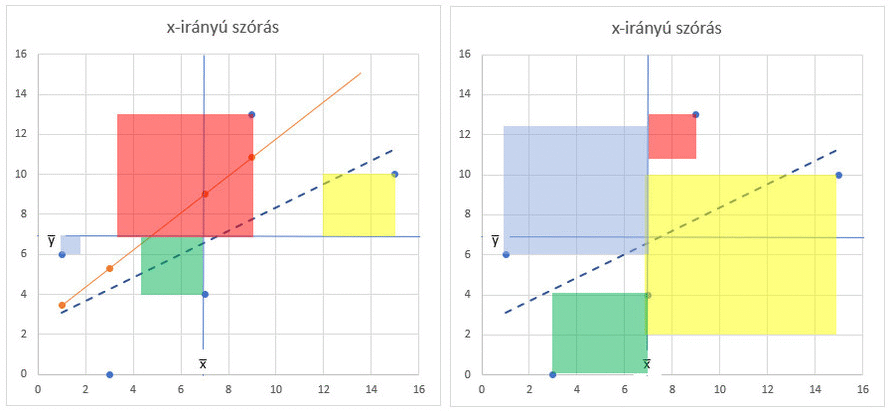
A négyzetek változása összességében egy kicsit kuszának tűnik az animált gif képen, de ha egyenként figyeled a négyzeteket, akkor könnyebben követhető azok változása. Az Sy / Sx hányados vonalának eltérése viszont jól megfigyelhető. A fentiek miatt sajnos a pontok szóródásának, azaz a korreláció erősségének mértékében korrigálni kell az egyenes meredekségét. Erre igazából a korrelációs együttható tűnt a legalkalmasabbnak és ha az Sy / Sx hányadost megszorozzuk a korrelációs együttható aktuális értékével, akkor a meredekség szépen visszatér középre és minden a helyére kerül.

Most igazából szabadkoznom kell, mert azt sajnos nem sikerült megfejtenem, hogy miért pont a korrelációs együttható alkalmas erre a feladatra, de a tapasztalat azt mutatja, hogy működik a dolog. Egyébként, ha rxy, Sy és Sx helyére behelyettesítjük a megfelelő képleteket, akkor – bár nem túl egyszerűen, de – levezethető a tankönyvekben leírt képlet.

Végül azért jussunk el oda, hogy ténylegesen meghatározzuk a keresett egyenes y = ax + b egyenletét, vagyis ehhez még ki kell számolnunk b értékét, azaz az egyenesünk eltolását az x és az y tengelyekhez képest. Ehhez elég annyit megtennünk, hogy a fenti képletbe behelyettesítjük az x̅ és az y̅ értékeit és kifejezzük b-t:

Ha megvan b értéke is, akkor már csak annyi a feladatunk, hogy a és b értékeit az egyenes egyenletébe behelyettesítve felírjuk az egyenes konkrét egyenletét.

Azt hiszem egyszerre ennyit elég lesz megemészteni. A folytatásban azt fogom elemezni, hogy miért fontos leellenőrizni, hogy a regressziós egyenes mennyire írja le jól a x és y összefüggését, illetve hogyan tudunk meggyőződni és döntést hozni az egyenes használhatóságáról, a későbbiekben pedig egy konkrét példán keresztül is be fogom mutatni a regressziós egyenes kiszámításának módját táblázatkezelőben és Minitab-bal is.