
Tegnap azért egy kicsit kiakadtam. Általában nem kezelem érzelmi kérdésként, ha valamit nem mond el a tanár, mert például nehezen érthető a levezetés vagy az adott információ ismerete nem ad hozzá többet a módszer gyakorlati alkalmazhatóságához. De olyannal még nem találkoztam, hogy egy adott dolognak a képletét mintha direkt olyan formában használná a statisztikával foglalkozók széles köre, ami nemhogy nem segíti, de kifejezetten gátolja a képlet hátterének megértését. Mindig van egy első eset, nekem pont ez volt az.
Konkrétan a korrelációs együttható kiszámításáról van szó.
Először is, mi is az a korreláció: A korreláció két tetszőleges adathalmaz közötti kapcsolat nagyságát és irányát (avagy ezek egymáshoz való viszonyát) jellemzi. Az általános statisztikai alkalmazás során a korreláció jelzi azt, hogy két tetszőleges érték nem független egymástól, azaz az egyik tényező értéke valamennyire függ a másik tényező értékétől. Két adathalmaz sokféle módon függhet egymástól. Elképzelhető, hogy semmilyen kapcsolat sincs a két jellemző között (1. ábra). Lehet közöttük lineáris pozitív korreláció, ami azt jelenti, hogy ha az egyik jellemző értéke nő, akkor a másik értéke is arányosan nőni fog (2. ábra). Lehet közöttük lineáris negatív korreláció, ha az egyik jellemző értéke nő, akkor a másik értéke arányosan csökken (3. ábra). Az is előfordulhat, hogy a két adathalmaz közötti kapcsolat nem lineáris, esetleg exponenciális vagy valamilyen speciális függvénnyel leírható kapcsolat van közöttük (4. és 5. ábra).

Amint az látható, két adathalmaz kapcsolatát pont-diagram (scatterplot) segítségével tudjuk ábrázolni. A pontdiagram létrehozásához szükségünk van egy olyan táblázatra, ahol a két jellemző értékei valamilyen szempont szerint össze vannak párosítva. Egy későbbi bejegyzésben majd látni fogjuk, hogy mondjuk a WTI és a Brent olaj árait egy olyan táblázatba fogom rendezni, amelyben az árak napi bontásban szerepelnek és a dátumok összekötik a két adatsor elemeit. Ellenkező esetben nehezen tudnánk eldönteni, hogy melyik WTI olajárhoz melyik Brent olajár tartozik, vagyis nem tudnánk eldönteni, hogy akkor most egy alacsony WTI olajárhoz az alacsony vagy a magas Brent olajár tartozik. Ha a kétféle olajár elemeit egymástól függetlenül összekeverjük és így próbáljuk meg ábrázolni ezek összefüggését, akkor egy olyan pontdiagramot fogunk kapni, amely nem mutat semmilyen összefüggést az adatok között.
Mivel a két adathalmaz elemeit párba állítjuk, a két adathalmaz elemeinek száma egyenlő kell, hogy legyen, ez előfeltétele a pontdiagram ábrázolásának és a korrelációs együttható kiszámításának is.
A korreláció mértékét a korrelációs együttható segítségével tudjuk jellemezni. A korrelációs együttható egy -1 és +1 közötti szám, amelynek értéke jelzi a korreláció irányát és erősségét.
- Ha a korrelációs együttható értéke közel van a +1-hez, akkor a két adathalmaz elemei között erős pozitív korreláció van: azaz, ha az egyik adatsor értéke nő, akkor a másik adatsor hozzá tartozó elemeinek értéke is nőni fog.
- Ha a korrelációs együttható értéke közel van a -1-hez, akkor a két adathalmaz elemei között erős negatív korreláció van: azaz, ha az egyik adatsor értéke nő, akkor a másik adatsor hozzá tartozó elemeinek értéke csökkenni fog.
- Ha a korrelációs együttható értéke közelít a nullához, akkor a két adathalmaz elemei között nincs lineáris kapcsolat.
A tapasztalati korrelációs együttható kiszámítása során tulajdonképpen egyfajta varianciát számítunk ki:
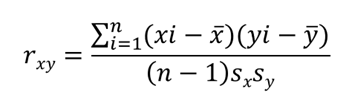
ahol
rxy – a korrelációs együttható
n – az x és y adathalmaz elemeinek száma
xi – az x adathalmaz i-dik eleme
yi – az y adathalmaz i-dik eleme
x̅ – az x adathalmaz elemeinek átlaga
y̅ – az y adathalmaz elemeinek átlaga
sx – az x adathalmaz szórása
sy – az y adathalmaz szórása
Ez egy nagyon szép képlet, de a laikus számára nem mond semmit. Sajnos ebben az esetben én is laikusnak számítottam, ezért elkezdtem utánanézni, hogy mit is jelenthet ez a képlet és miért pont így számítjuk ki ezt a csodálatos együtthatót. Néztem az internetet és a statisztika tankönyveket és egy ideig sehol sem találtam értelmes magyarázatot a korrelációs együttható működésére vonatkozóan. És egyszer csak megvilágosodtam!
Hello! Ezt a képletet nem így használták, illetve nem így írták eredetileg! Hanem így:
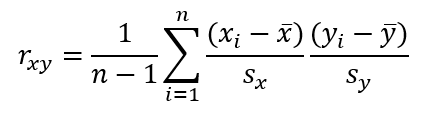
Ok, a laikusnak még mindig nem mond sokat a dolog, de legalább most már eljutottam odáig, hogy el tudom magyarázni a képlet működését. És lőn…
Figyelmes szemlélő felfedezheti, hogy a két képlet teljesen megegyezik, csak a felírás formája más. Viszont az adatokat így csoportosítva minden elem különös jelentést nyer. Ezt viszont egy egyszerű példa segítségével tudom igazán jól elmagyarázni:
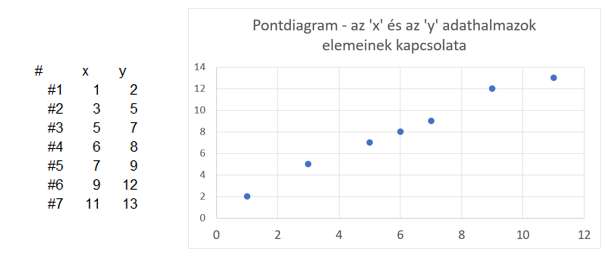
Tegyük fel, hogy van két darab hételemű adathalmazunk szépen párba rendezve. Ezt az adatsort ábrázoltam is egy grafikonon:
Mivel a képletben szükségem lesz rá, ezért kiszámoltam az ’x’ és az ’y’ adathalmazok átlagát és szórását is:
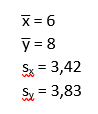
Akkor most húzzunk egy függőleges vonalat az x̅-hoz és egy vízszintes vonalat az y̅-hoz. A két átlag jól láthatóan négy részre osztotta fel a diagram területét aszerint, hogy az egyes pontok távolsága az x̅-tól és az y̅-tól pozitív vagy negatív előjelű.
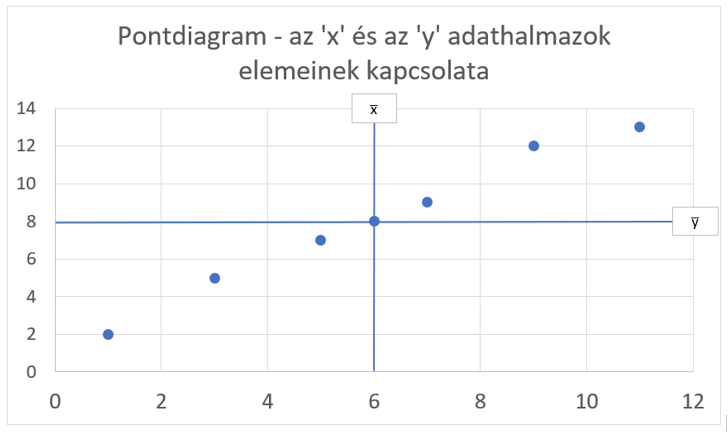
Például a képen látható pont esetében a pont távolsága negatív előjelű mindkét átlag esetében. Ha a két távolságot összeszorozzuk, akkor negatív számot negatív számmal szorozva egy pozitív számot fogunk kapni.
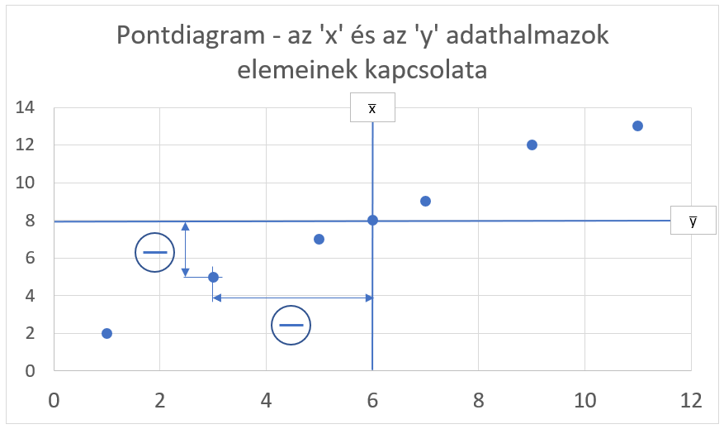
Ha lenne egy olyan pontunk, amelynek távolsága az x̅-tól pozitív, az y̅-tól pedig negatív, akkor a kettő szorzata egy negatív szám lenne.
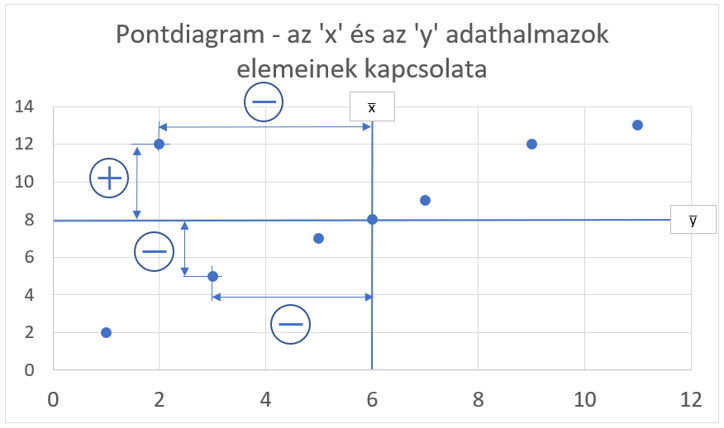
Ha tehát a szorzatok szempontjából vizsgáljuk az így felosztott diagramunkat, akkor azt láthatjuk, hogy a pontoknak az x-, és y-átlagoktól mért távolságainak szorzatai attól függően lesznek pozitívak vagy negatívak, hogy a diagram melyik negyedébe esnek. Minden egyes pont, amely egy pozitív negyedbe esik növelni fogja a korrelációs együttható értékét és minden olyan pont, amely egy negatív negyedbe esik, csökkenteni fogja a korrelációs együttható értékét, hiszen végső soron itt egy összegről beszélgetünk.
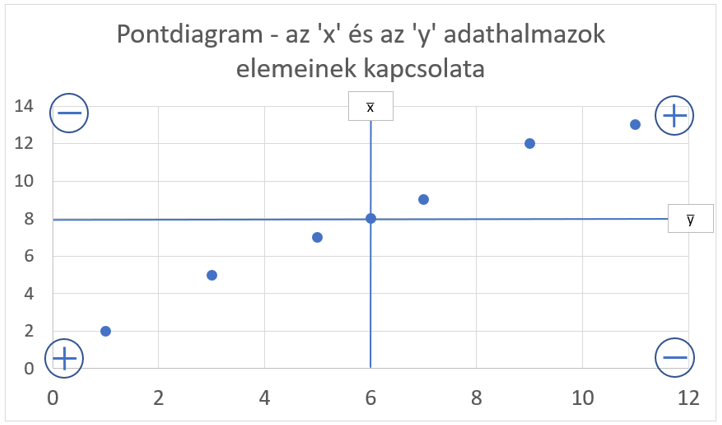
Ameddig most eljutottunk az a következő:

Mint látható, ezt a jellemzőt másképpen jelöltem (rxy helyett COVxy), mert ezt nem korrelációs együtthatónak, hanem kovarianciának hívjuk. Ezt a jellemzőt önmagában ritkán használjuk, de a későbbiekben jó néhány más statisztikai eszköz alkalmazásakor előjön majd ez a képlet.
És most jöjjön az utolsó lépés. Merthogy a korrelációs együttható esetében nemcsak egyszerűen vesszük pontok megfelelő irányú távolságát az átlagoktól, hanem először átszámoljuk ezt a távolságot egy más koordináta rendszerbe! Mivel a két adathalmaz szórása nem egyezik meg, ezért az x-, és az y-tengely „osztása” nem egyezik meg, tehát ha összeszorozzuk egy pont távolságait az x̅-tól és az y̅-tól, akkor tulajdonképpen almát a körtével szorzunk össze!
Készítsünk egy olyan koordináta rendszert, amelynél az x-tengely és az y-tengely beosztása nem egyezik meg, az x-tengely egy osztása egyezzen meg az ’x’ adatsor szórásával, az y-tengely egy osztása pedig egyezzen meg az ’y’ adatsor szórásával!
Ehhez nem kell mást tennünk, minthogy elosztjuk a pont x̅-tól mért távolságát az ’x' adatsor szórásával, az y̅-tól mért távolságát pedig az ’y’ adatsor szórásával. Ezen a ponton pillantsunk vissza a korrelációs együttható előbb felvázolt képletére!
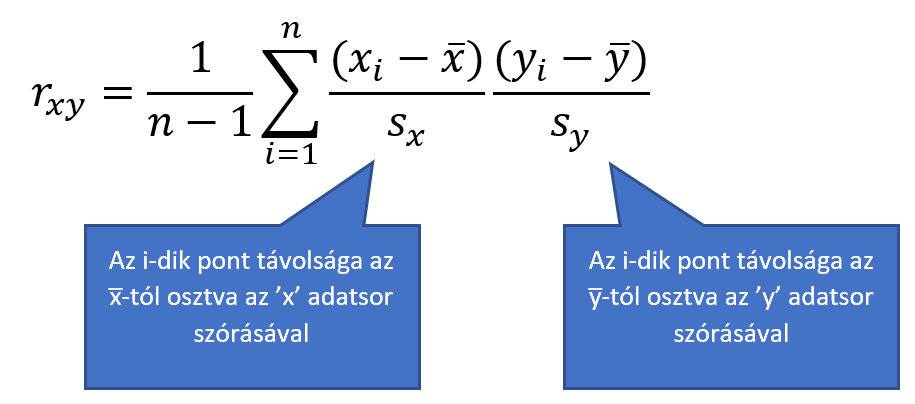
Összegezve az eddigieket azt mondhatjuk, hogy amikor kiszámoljuk a korrelációs együtthatót, akkor
- Kiszámoljuk minden pont esetében, hogy milyen irányban hány „szórásnyira” van az x̅-tól és az y̅-tól, majd ezeket minden pont esetében összeszorozzuk.
- A pontonként kapott szorzatokat összeadjuk,
- majd elosztjuk n – 1-gyel. Hogy miért nem n-nel, azt egy korábbi bejegyzésben már tárgyaltam.
Amikor átszámítjuk a pontok távolságait a szórásokkal arányosított koordinátarendszerbe, azt úgy nevezik a művelt statisztikusok, hogy kiszámítják a távolságok Z-pontszámát (Z-score).
Hogyan is néz ki ez a grafikonunkon?
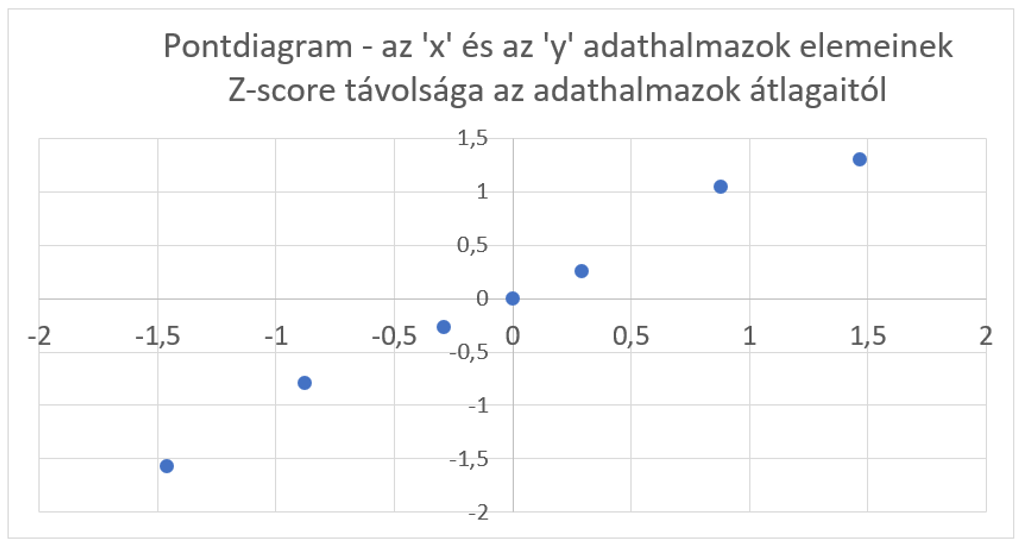
Akkor most nézzük meg, hogy mit kaptunk eredményül (bocs, de ezt már kiszámoltam táblázatkezelő programmal):

ahol
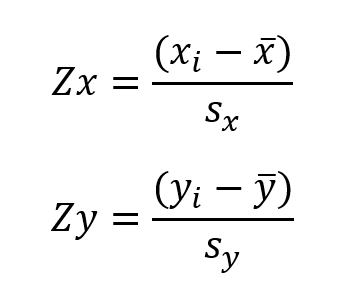
és
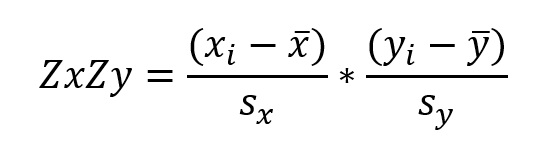
Amint az a diagram alapján várható volt, a korrelációs együttható közel 1, tehát az ’x’ és az ’y’ adatsorok között erős pozitív korreláció van.
Összegzés: Nem tudom, hogy ki és mikor alakította át a fent ismertetett képletet arra, amivel lépten-nyomon találkozni lehet, de semmiképpen sem tartom jó ötletnek. Nyilvánvaló a számomra, hogy a fent említett levezetés is igényel egy bizonyos fokú befogadókészséget a hallgatóktól, de az összefüggések ilyen típusú vizuális megjelenítése sokat segít az összefüggések megértésében és így a korreláció elemzés gyakorlati alkalmazásában, illetve az eredmények értelmezése terén is.





