Végre eljutottam ahhoz a témához, ami miatt ez a kis kalandozás elkezdődött. A sorozat első cikkében (Végre megtaláltam a Szent Grált!) már említettem, hogy erre a szimulációra úgy bukkantam rá, hogy arról kerestem valamilyen érthető irodalmat, hogy mi is a probléma a p-értékkel (A titokzatos P színre lép – Mi az a P-Value?). Merthogy

Houston, we have a problem!

A p-érték egy széleskörben alkalmazott mutatószám arra vonatkozóan, hogy egy statisztikai teszt eredménye mennyire szignifikáns, nagyon sok esetben ez alapján tudjuk eldönteni, vajon elfogadjuk-e a nullhipotézist vagy inkább elutasítsuk. Ezt a p-értéket nagyjából mindenki irányadónak tekinti és elhisszük neki, amit állít. Azonban vannak olyan helyzetek, amikor a p-érték is megcsalhat minket.

Nézzük meg ezt egy példán. Tegyük fel, hogy adott egy sokaságunk, amelynek az átlaga 51, de ezt mi nem tudjuk. Azt feltételezzük, hogy a sokaságunk átlaga 50, ezt szeretnénk bizonyítani, vagy elvetni. Az 51 és az 50 között nem nagy az eltérés, ezt a kis eltérést akár még kerekítési hibának is felfoghatjuk. Mivel a sokaságot nem ismerjük, ezért kiveszünk belőle egy mintát és a minta tulajdonságai alapján próbálunk következtetni a sokaság tulajdonságaira.

Elvégzünk egy hipotézis vizsgálatot (lásd a következő ábra bal alsó sarkában) amely esetében a nullhipotézis az, hogy a sokaság átlaga 50. Kiszámítjuk a p-értéket és azt látjuk, hogy több, mint 50% az esélye annak, hogy ennél a mintánál extrémebb mintát is ki tudnánk venni a sokaságból. Vagyis hátradőlhetünk és elfogadva a nullhipotézist kijelenthetjük, hogy nincs bizonyítékunk arra, hogy a mintát nem egy olyan sokaságból vettük ki, amelynek az átlaga 50.

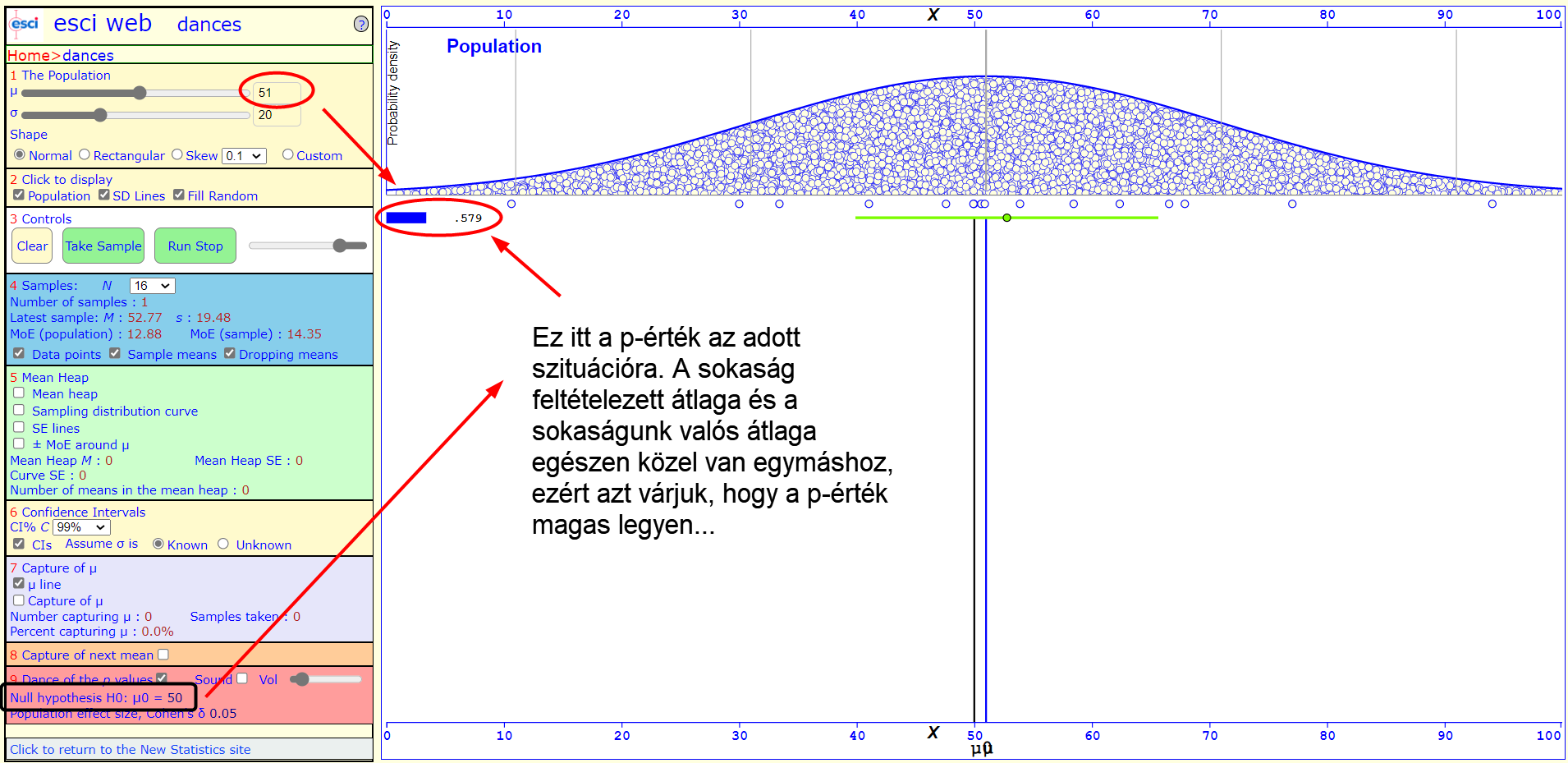
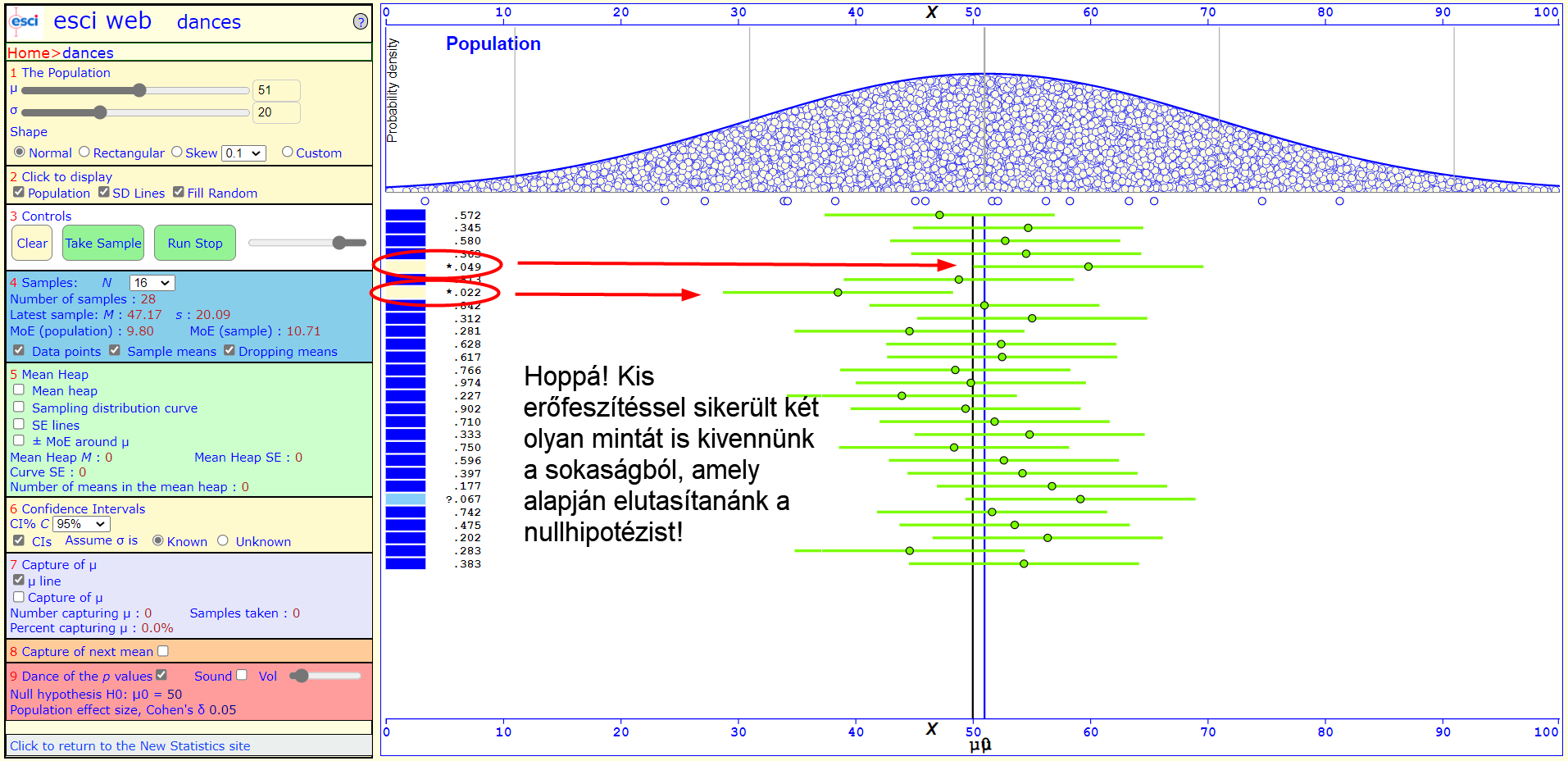
Vegyünk még néhány mintát. Sajnos, ha több mintát is veszünk a sokaságból, akkor azért a p-érték meg is tréfálhat minket, ...

... sőt, ha egy kicsivel több erőfeszítést is beleteszünk a történetbe, akár olyan esetekbe is belefuthatunk, amikor a p-érték alapján hibás döntést hozunk annak ellenére, hogy elvileg minden óvintézkedést megtettünk! És akkor még el is mondhatjuk azt, hogy a sokaság valós átlaga egészen közel van a feltételezett átlaghoz!

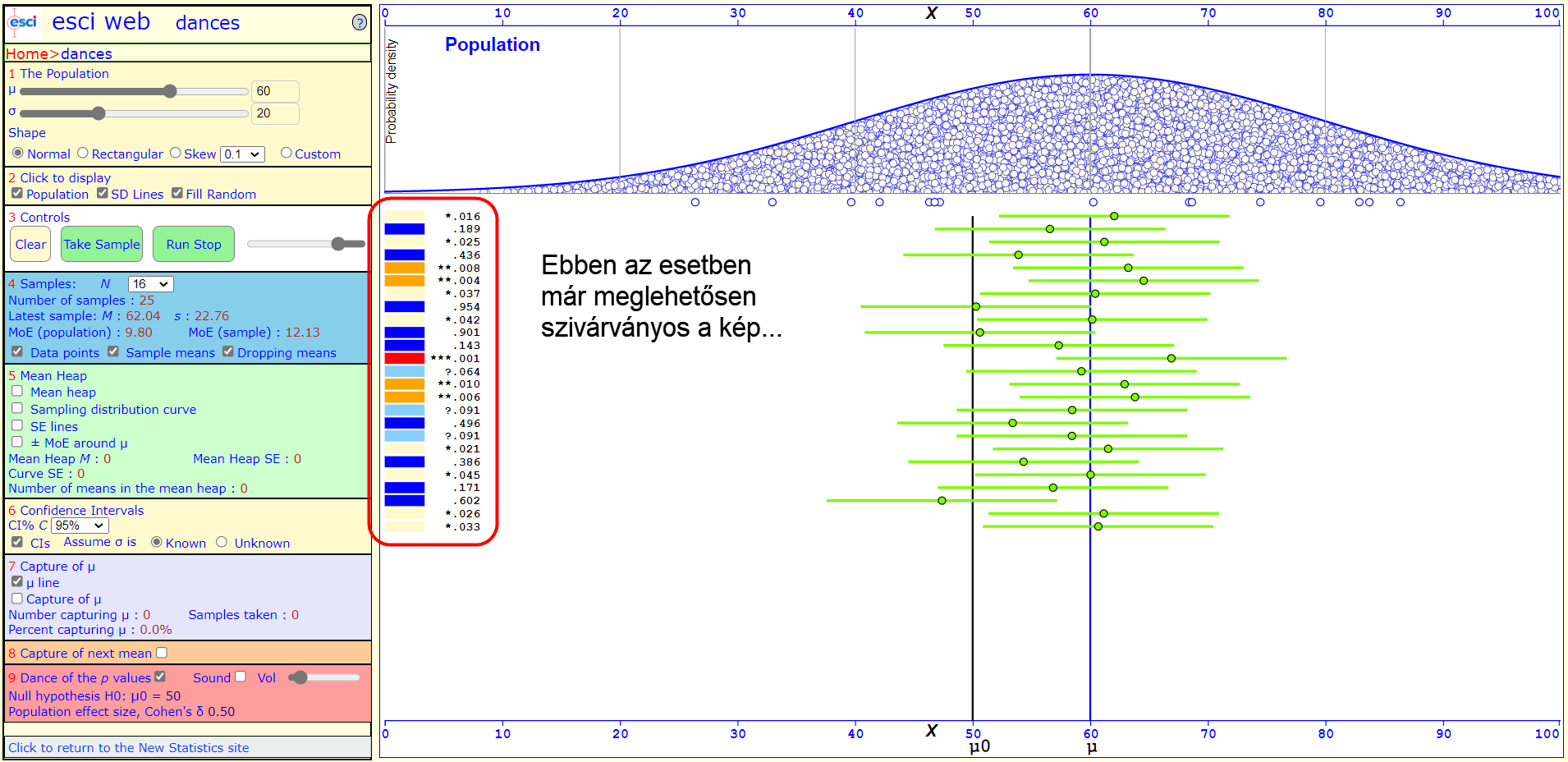
Mi történik akkor, amikor a sokaság feltételezett és valós átlaga között egy leheletnyivel nagyobb a különbség? Sajnos a p-érték alapján történő döntés ez esetben meglehetősen megbízhatatlanná válik, mert a döntésünk eredménye erősen attól fog függeni, hogy milyen mintát sikerült kivenni a sokaságból. 

Persze amennyiben a sokaság valós, illetve feltételezett átlaga között elég nagy az eltérés, ott már aránylag újra biztos talajon mozgunk, de azért még itt is érhetnek minket meglepetések. Mindez úgy, hogy közben a minták jelentős többsége esetében a p-érték 0!

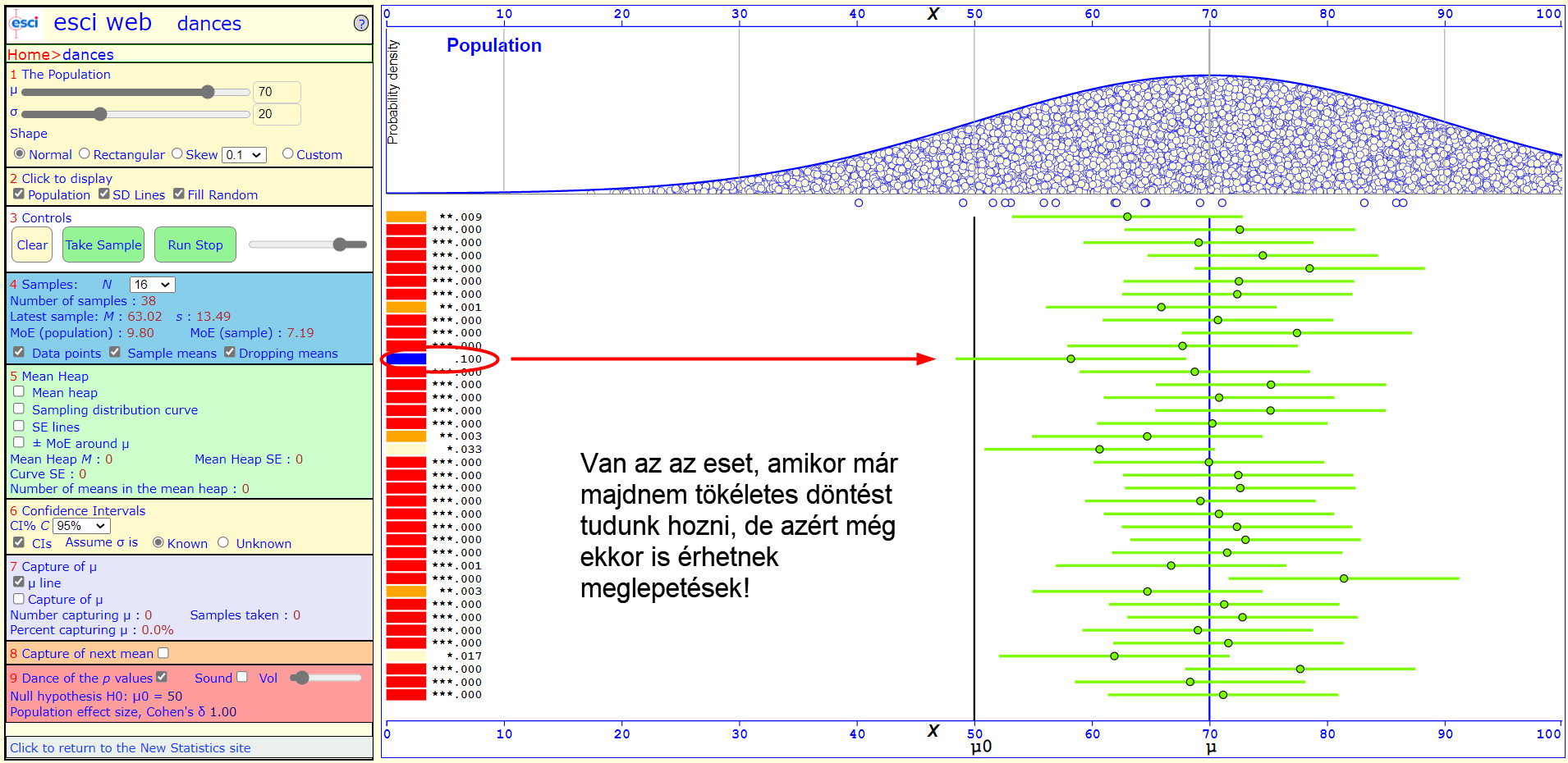
A végső következtetés sajnos az, hogy a fenti információk birtokában a p-érték hitelességében még akkor is nehéz hinni, ha az értéke szélsőségesen nagy, vagy szélsőségesen kicsi. De akkor mit tehetünk?

Hát, persze! A jó öreg mintaelemszám növelés itt is a segítségünkre siet...

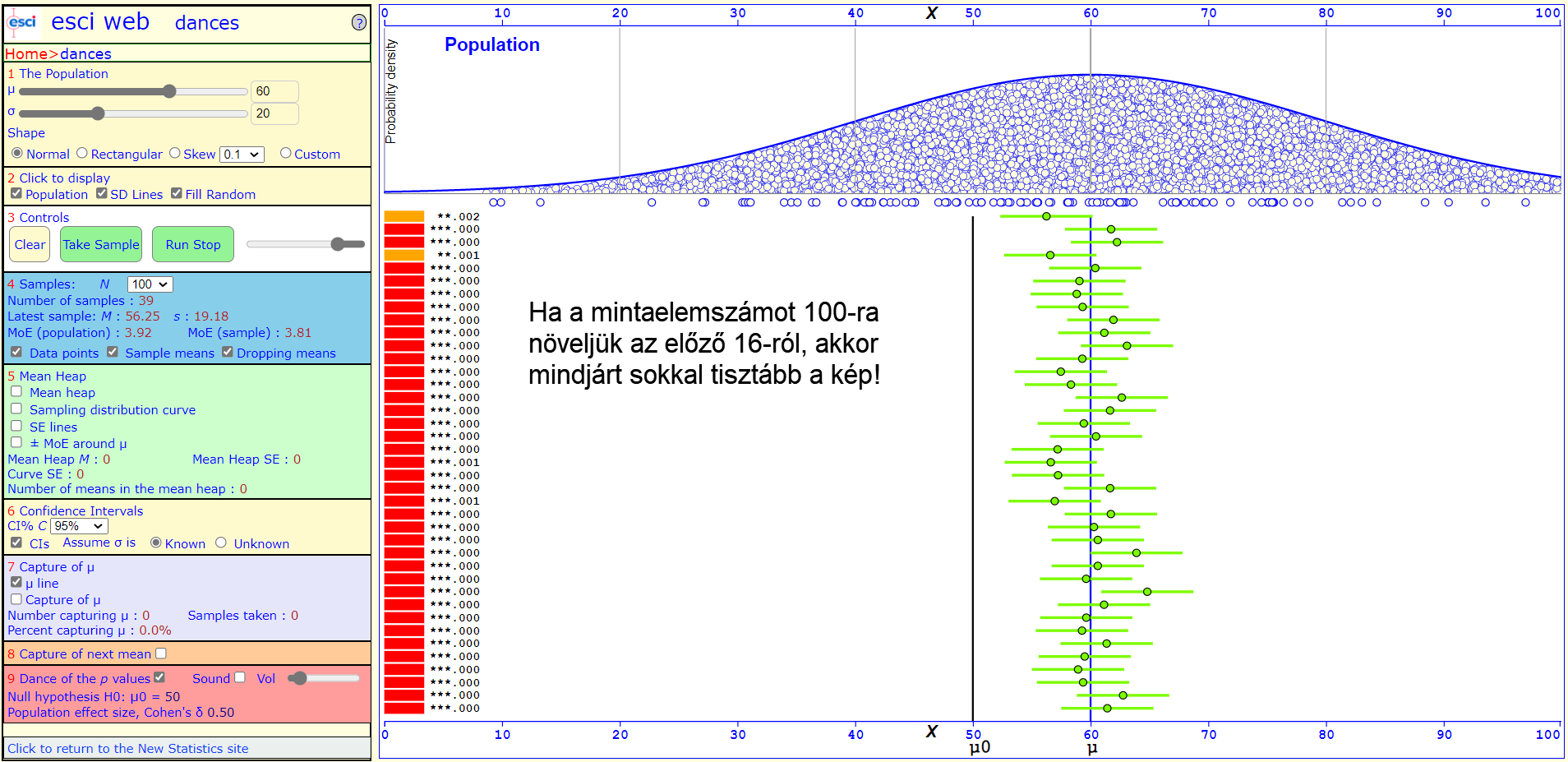
Az egyik előző esethez hasonlóan, amikor a sokaság valós átlaga 60 volt, a hipotézisünk pedig 50, akkor 16-elemű minták esetében igencsak szivárványos volt a kép. Ha a minták elemszámát 100-ra növeljük, a szituáció teljesen egyértelművé válik és a korábbi bizonytalanság megszűnik.

Hasonló eredményt kapunk, ha a legelső példánkat vizsgáljuk meg a megemelt mintaelemszámokkal.

Egy probléma azért mégiscsak maradt, mégpedig az, hogy a valóságban sohasem ismerjük a sokaság valós átlagát (és általában az egyéb tulajdonságaikat sem). Vagyis igencsak nehéz egy tesztről eldönteni, hogy vajon mekkora veszély fenyeget minket azzal kapcsolatban, hogy téves döntést hozunk. Ezért aztán nem egyszerű azt sem eldönteni, hogy vajon hány elemű mintát is kellene kivennünk ahhoz, hogy biztonságban érezhessük magunkat.

 De erről majd később...

Források:

Geoff Cumming & Robert Calin-Jageman: Introduction to the new statistics: Estimation, Open Science, and Beyond, Routledge Subs. of International Thomson Org. 29 West 35th Sreet New York, NYUnited States, October 2016
ISBN:978-1-138-82552-9

Geoff Cumming youtube-csatornája
https://www.youtube.com/channel/UCwRbwVb6mRKuyXtV1td-vig