
Két egymástól független adathalmaz esetén felmerül ugyanaz a kérdés, amelyet korábban az egymintás tesztek esetében (A t-próba elegendő bizonyíték?) más feszegettem. Tegyük fel, hogy adott két minta, amelyről azt gyanítjuk, hogy ugyanabból a sokaságból származnak. Lefuttatjuk a kétmintás t-próbát (Amikor túl kevés a vizsgálandó minta…), amely szerint a minták átlaga megegyezik. Viszont mi történik akkor, ha a minták átlaga megegyezik, de a szórása, illetve a varianciája különbözik?
Ha csak két mintánk van, akkor a legegyszerűbb teszt a minták varianciáinak összehasonlítására a kétmintás F-próba. A kétmintás F-próba esetében a két minta varianciájának hányadosát vizsgáljuk és arra vagyunk kíváncsiak, hogy a két variancia HÁNYADOSA megegyezik-e 1-gyel. Azt már korábban tisztáztuk, hogy egy sokaság és a belőle kivett minták varianciáinak hányadosai Khí-négyzet eloszlást követnek. De mi történik akkor, ha két ilyen hányadost osztunk el egymással?
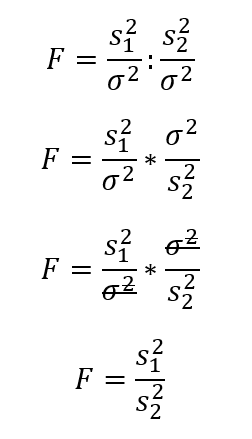
ahol természetesen s1² az egyik minta, s2² pedig a másik minta, σ² pedig a sokaság varianciája. A hányados egy speciális eloszlás, a Fischer – Snedecor F-eloszlás szerint változik, ha a minták ugyanabból a sokaságból, vagy egymással megegyező sokaságokból származnak. Az F-eloszlás definíció szerint két Khí-négyzet eloszlású változó hányadosának eloszlása. A hipotézis vizsgálathoz szükséges kritikus határértéket a t-eloszláshoz hasonlóan táblázatból tudjuk kikeresni. A kikereséshez szükséges tudnunk, hogy az F-eloszlásnak nem egy, hanem két paramétere van.
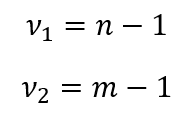
ahol ‘n’ az egyik minta, ‘m’ pedig a másik minta elemszáma. Az F-eloszlás táblázat így néz ki.
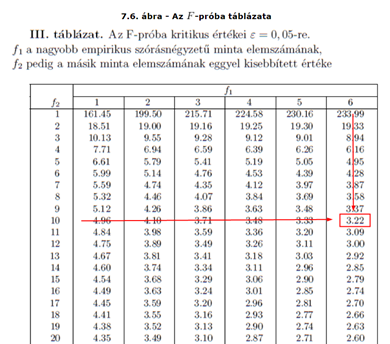
/forrás: https://gyires.inf.unideb.hu/KMITT/b21/ch07s07.html/
Mivel az F-eloszlás értéke a két minta elemszámától függ, így a táblázat jelen esetben a 95%-os megbízhatósági határértékhez tartozik. Vagyis, ha van egy 11 és egy 7-elemű mintánk, akkor a 95%-os megbízhatósági határ az f1 = 6 és az f2 = 10 értékekhez tartozó számot kell kiválasztanunk, amely ez esetben 3,22 lesz.
R-ben korábban már említettem egy ‘var.test()’ nevű függvényt, amely pontosan ezt a tesztet végzi el. Szerencsére a függvény alkalmazásához nem szükséges semmilyen extra csomagot betökteni, az R alapcsomagja tartalmazza ezt. Nézzük meg, hogyan működik. A függvény működésének bemutatásához létrehoztam három mintát.
#A három minta létrehozása
minta1 <- rnorm(50, mean = 0, sd = 1)
minta2 <- rnorm(50, mean = 0, sd = 1.1)
minta3 <- rnorm(50, mean = 0, sd = 3)
A három minta átlaga megegyezik. Az első két minta (‘minta1’ és ‘minta2’) szórása is nagyon hasonló, a harmadik minta (‘minta3’) szórása viszont jelentésen eltér az első kettőétől. A három mintát kezelhetném különálló vektorokkal is – úgy. ahogyan most vannak. De lassan közeledünk azon módszerek felé, ahol már szükségünk van arra, hogy az adatokat egyben, többdimenziós “adattáblákban” kezeljük. Erre az első példa, hogy a három minta tulajdonságait egy dobozdiagramon is szeretném megmutatni, viszont ahhoz, hogy mindhárom mintát egy diagramon tudjam elhelyezni, a három mintát egy adattáblában kell elhelyeznem, nem is akármilyen formában.
#A három minta összefűzése egy adattáblába
mintak <- data.frame(minta1, minta2, minta3)
#Az adattábla átrendezése a boxplot kedvéért
mintak2 <- tidyr::gather(data = mintak,
key = "mintaKulcs",
value = "adat",
minta1, minta2, minta3)
Először is a ‘mintak’ nevű adattáblába összevontam a három minta adatait három különálló oszlopként. Ezután a ‘mintak2’ adattáblában ezeket úgy rendeztem át, hogy mind a három minta elemei egy oszlopba (adat) kerüljenek egymás alá, illetve létrehoztam egy másik oszlopot (‘mintaKulcs’), amelyben az egyes minták azonosítói szerepelnek (‘minta1’, ‘minta2’, ‘minta3’).

Így most már előállt az a “tidy”, azaz rendezett táblázat, amelynek a használatával egyszerűen létre tudom hozni a dobozdiagramot.
#A ggplot2 csomag betöltése
library(ggplot2)
#Boxplot megrajzolása
ggplot(mintak2, aes(x = mintaKulcs, y = adat)) +
geom_boxplot() +
labs(title = "A három minta") +
theme(axis.title.x = element_blank())
A “boxplot” megrajzolásához ezt a bizonyos ‘mintak2’ adattáblát használtam fel, az x-tengely jelöli az egyes mintákat a ‘mintaKulcs’ mező alapján, az y-tengelyen az adatok kerültek ábrázolásra. Ezután a ‘geom_boxplot()’ függvény segítségével megrajzoltam a dobozdiagramot, majd a már jól ismert ‘labs()’ függvénnyel címet adtam a diagramnak. Az utolsó sorban eltüntettem az x-tengely feliratát, hogy a diagram áttekinthetőbb legyen. És itt az eredmény.
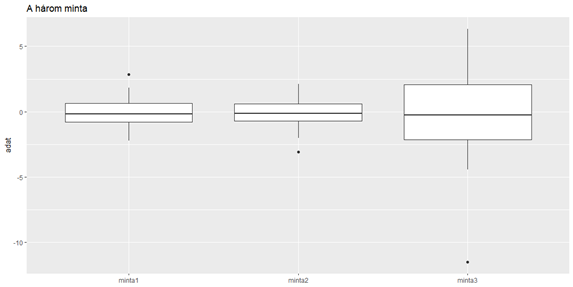
Elkészültek a vizsgálandó minták, most jöhetnek a kétmintás F-próbák. Először hasonlítsuk össze az első és a második mintát. Mivel ez alkalommal párosával fogom összehasonlítani a mintákat, ezért a ‘mintak’ adattáblát fogom alkalmazni, így az egyes mintákat meg tudom hivatkozni az oszlopok nevével. Mivel a “data = mintak” paraméterrel megadtam, hogy melyik adattáblát fogom vizsgálni, ezért az x és az y paraméterek esetében elég egyszerűen az oszlopnevekre hivatkozni.
varTest1 <- var.test(data = mintak,
x = minta1,
y = minta2,
ratio = 1,
conf.level = 0.95)
varTest1
A ‘varTest1’ változóba kerül az első két minta varianciájának összehasonlítása. A teszthez a ‘mintak’ adattáblát használom fel, ezt adtam meg a ‘data = mintak’ paraméterrel. A teszt során az adattábla ‘minta1’ és ‘minta2’ oszlopait fogom összehasonlítani. A ‘ratio = 1’ azt jelenti, hogy azt vizsgálom, hogy a két minta varianciájának a hányadosa 1, vagy sem. Így például lehetne azt vizsgálni, hogy a két minta hányadosa lehet-e 0,8 vagy 1,2 is… A ‘conf.level = 0.95’ paraméterrel pedig megadtam, hogy a teszt megbízhatósági határa legyen 95%.
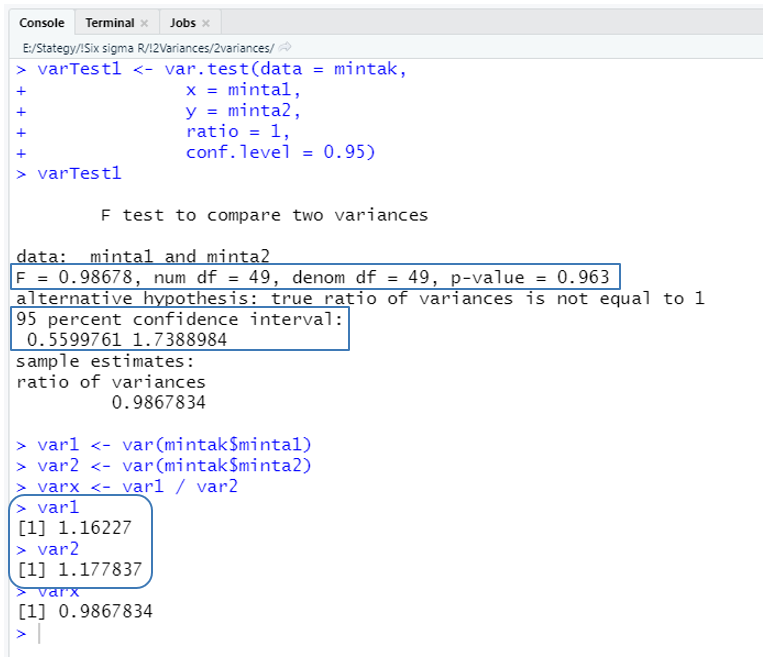
A teszt címe után megadásra került, hogy a ‘minta1’ és a ‘minta2’ adatsorokat hasonlítottuk össze. Az ‘F = 0.98678’ a két minta varianciáinak hányadosa, azaz 1,16227 / 1,177837 = 0,98678. Mivel mindkét minta 50 elemből áll, ezért mind a számláló, mind a nevező szabadsági foka 49-49. A 95%-os megbízhatósági tartomány (95 percent confidence interval → 0,55997 – 1,7388) magában foglalja az 1-et, vagyis nem zárható ki, hogy a tört értéke felveheti az 1-et.
A ‘p-value = 0.963’ értéke azt jelzi, hogy a p-érték nagyobb, mint 0,05, ezért a nullhipotézist elfogadjuk és a teszt eredményeként megfogalmazzuk, hogy nincs elegendő bizonyíték arra, hogy a két minta varianciája nem egyforma, vagyis a két sokaság, amelyekből a mintákat kivettük, eltérne ebből a szempontból. Most nézzük meg ugyanezt a ‘minta1’ és a ‘minta3’ adatsorokra.
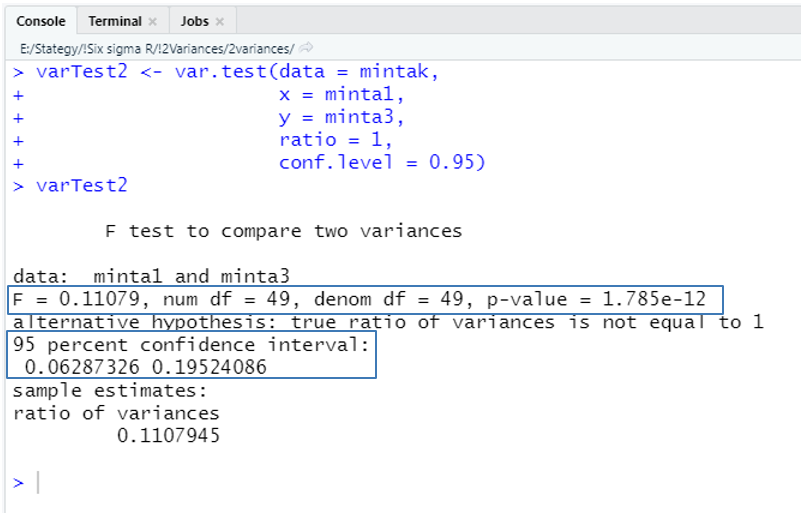
varTest2 <- var.test(data = mintak,
x = minta1,
y = minta3,
ratio = 1,
conf.level = 0.95)
varTest2
Az eredmény azt mutatja, hogy a két minta varianciája jelentősen eltér, hiszen a ‘p-value’ értéke jóval kisebb, mint 0,05, vagyis 5%-nál kisebb az esélye, hogy a két sokaság varianciája, amelyből a mintákat kivettük, megegyezik. A 95%-os megbízhatósági tartományban (95 percent confidence interval → 0,06287 – 0,19524) az 1 nincs benne, ezért ezt az értéket 95%-os valószínűséggel nem veheti fel a két minta varianciáinak hányadosa. Ez alapján a nullhipotézist, mely szerint a ‘minta1’ és a ‘minta3’ adatsorok varianciája megegyezik elvetjük és elfogadjuk az ellenhipotézist, mely szerint a két minta varianciája eltér, azaz a mögöttük álló kétsokaság varianciája is nagy valószínűséggel különbözik egymástól.
Ez a teszt nagyon egyszerű, de sajnos a tudósok bebizonyították, hogy csak akkor működik helyesen, ha a két összehasonlítandó minta mögött álló sokaságok normál, vagy legalábbis valamilyen szimmetrikus eloszlást követnek. Erősen aszimmetrikus eloszlások, vagy kieső értékek esetén ez a teszt nem megfelelő eredményt ad.
----------------------
Két minta varianciájának összehasonlítására alkalmazható még a Wald-teszt is, amely esetében a próbastatisztika képlete bizonyos szempontból hasonlít a Welch-próba képletére (Minden „sikeres” minta mögött áll egy sokaság – Kétmintás t-próba R-ben).
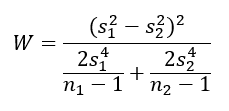
ahol, s1² és s2² a két minta varianciája, n1 és n2 pedig a két minta elemszáma. A W változó egy df = 1 szabadsági fokú Khí-négyzet eloszlást követ, így a próba határértékét ez alapján kell meghatározni. A Wald-teszt egy tulajdonképpen a korábban ismertetett Z-, illetve t-próbák egy általánosabb formája, ahol mindegyik esetben egy paraméter (átlag, szórás, variancia, stb.) becsült, illetve elméleti értékeinek “távolságát” vizsgáljuk, amelyet a becsült paraméter varianciájával súlyozunk.
Sajnos nincs olyan kész függvény R-ben, amely ezt a tesztet ebben a formában megvalósítaná, legalábbis én nem találtam, de ha te tudod a módját, kérlek oszd meg velem kommentben. Természetesen lehet írni egy olyan kis programot R-ben, amely képes kiszámítani a próba statisztikát, ezt talán majd egyszer megteszem, ha lesz rá igény.
----------------------
Mivel a Wald-teszt próba statisztikája Khí-négyzet eloszlású, amelyről tudjuk, hogy erősen a normál eloszláshoz kötődik (Khí-négyzet eloszlás – Na, már megint egy újabb eloszlás!), ezért ennek a tesztnek is ugyanaz a hátránya, mint az F-próbának. Azt feltételezi, hogy a sokaságok, amelyekből a mintákat kivettük, normál eloszlásúak, alkalmazása nem normál eloszlású sokaságok esetében hibás döntésekhez vezethet.
Kettő, de akár három vagy több minta vizsgálata esetében jól alkalmazható a Bartlett-teszt, amelynek a próbastatisztikája bonyolultabb, mint a fentebb ismertetett F-próbáé.
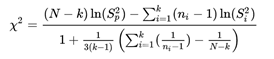
ahol
N - az összes minta összes elemének mennyisége, vagyis ha mondjuk van 3 darab 10-elemű mintánk, akkor N = 3 * 10 = 30.
k - az egymástól független minták száma,
ni – az egyes minták elemeinek a száma,
Sp² - az összes minta összes elemének az összegzett varianciája,
Si² - az egyes minták elemeinek varianciája.
A próba statisztika képlete elsőre bonyolultnak tűnik (mondjuk ki nyíltan, elég komoly hieroglif tulajdonságokkal rendelkezik), de végül is nem olyan vészes az egész. A képlet számlálója tulajdonképpen egy hányados.
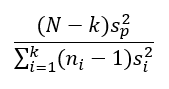
Adott ‘k’ darab mintánk, amelyről el szeretnénk dönteni, hogy a varianciáik megegyeznek-e vagy sem. Az első minta elemszáma ‘n1’, a másodiké ‘n2’, és így tovább, a k-dik minta elemszáma ‘nk’. Az összes minta elemszáma ‘N’.
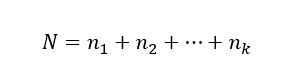
A tört számlálójában sp² az ‘N’ darab mintaelem összegzett varianciája (within variance), amelyet súlyozunk az ‘N’ mintaelemből számolt szabadsági fokok számával. ‘N’-ből azért vonjuk ki a ‘k’-t, azaz a minták darabszámát, mert minden egyes mintának van egy darab függő értéke. A nevezőben az egyes mintákra kiszámított varianciák (between variances) összege szerepel. Azért, hogy a minták elemszámainak ne kelljen megegyeznie, a tört a varianciáknak a minták elemszámaival súlyozott értékét veszi figyelembe.
Vagyis tulajdonképpen kétféle módon számoljuk ki ugyanannak az adatsornak a varianciáját, és ezt hasonlítjuk össze. Tegyük fel, hogy a teljes adatsor elemei egyenletesen oszlanak el a ‘k’ darab minta között, vagyis a minták varianciái körülbelül megegyeznek egymással. Ez esetben az összegzett variancia körülbelül azonos lesz a mintákra kiszámolt egyedi varianciákkal. Ha egy vagy több minta varianciája lényegesen kisebb vagy nagyobb a többiekénél, akkor a nevezőben a minták varianciáinak súlyozott összege is kisebb vagy nagyobb lesz a mintaelemek összegzett varianciájánál.
Persze az egy sokaságból kivett minták varianciái nem pontosan fognak megegyezni, csak úgy körülbelül. Így a kihívás abban van, hogy mekkora lehet a különbség a minta varianciák és az összegzett variancia között, ahol már nem hisszük el, hogy a minták varianciái megegyeznek.
Ez tulajdonképpen egy olyan teszt, amelyet likelihood hányados próbának (likelihood ratio test) hívnak, elvileg azt vizsgálja, hogy két egymással versengő feltélelezés (hipotézis, vagy statisztikai model) vajon mennyire hasonlít egymásra az alapján, hogy mennyire kapjuk ugyanazt az eredményt a használatukkal. Viszont, mivel a hányados maximumát keressük, ezért érdemes a hányados logaritmusával számolni, mert így a hányadosból egy különbség lesz, és az így kapott különbségnek könnyebb megtalálni a maximumát. Ezt használjuk ki a maximum likelihood módszer esetében is (Ruhát a meztelen királyra! – Maximum Likelihood becslés).
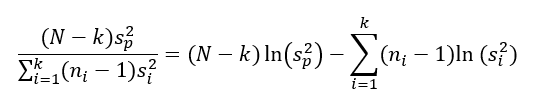
Ezek szerint a próbastatisztika számlálójának jelentését tisztáztuk.
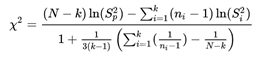
A próbastatisztika nevezőjéről csak annyit illik tudnunk, hogy ez egy módosító tényező, amellyel azt érjük el, hogy a Khí-négyzet próbastatisztika ‘k-1’ szabadsági fokú Khí-négyzet eloszlású legyen, ha a nullhipotézis, miszerint az összes minta ugyanabból a sokaságból, vagy egymással megegyező sokaságokból származik.
A Bartlett-tesztet egyszerűen el tudjuk készíteni R-ben, ráadásul egyetlen extra csomagot sem kell betöltenünk emiatt, mert a ‘bartlett.test()’ függvény az R alapcsomagjának része. A függvény működésének bemutatásához a cikk elején létrehozott ‘minták2’ nevű adattáblát fogom felhasználni.
bartlett.test(adat ~ mintaKulcs, data = mintak2)
A függvény második paramétere (“data = mintak2”) a teszt elvégzéséhez felhasználandó adattáblát adja meg. Az első paraméter viszont (“adat ~ mintaKulcs”) egy érdekes adatmegadási forma, amelyet az R előszeretettel alkalmaz adattáblák mezőinek megadása esetén. A kifejezés körülbelül azt jelenti, hogy az ‘adat’ oszlop mezői a ‘mintaKulcs’ oszlopban szereplő kategóriák szerint csoportosítva.
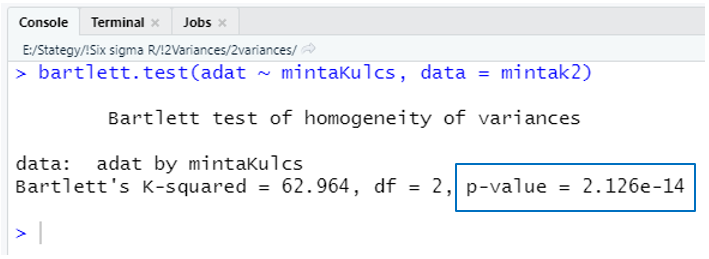
A “Bartlett’s K-squared = 62.964” értelemszerűen a Khí-négyzet próbastatisztika, azaz a fentebb részletesen ismertetett bonyolult képlet eredménye. A “df = 2” a szabadsági fokok száma, amely ez esetben 2, mivel 3 vizsgált mintánk van és ahogy azt fentebb említettem, a próba határértéke mindig eggyel kevesebb a minták számánál. Nem meglepő, hogy a ‘p-value’ értéke egy igen kicsi szám lett, hiszen tudjuk, hogy az egyik mintánk varianciája jelentősen nagyobb, mint a másik kettőé. Arra viszont sajnos nincs megoldás, hogy megtudjuk, konkrétan melyik mintánk lóg ki a sorból, csak azt tudjuk meg, hogy megegyeznek a mintáink varianciái, vagy nem. Ráadásul itt is a korábbiakhoz hasonló problémába ütközünk, a Bartlett-teszt is csak közel normál eloszlású sokaságok esetén működik megfelelően.
----------------------
Így végül elérkeztünk a teszteknek ahhoz a csoportjához, amelyet leginkább alkalmazni szoktunk. Ezt összefoglaló néven Levene-tesztnek szokták becézni, de ez tulajdonképpen nem egy teszt, legalább három különböző tesztet is ezzel a névvel szoktak illetni. A teszt alapelvét már egy korábbi cikkben ismertettem (Sűrű szirupban is lehet gyorsan úszni? – Adatsorok varianciájának összehasonlítása), ezt most annyival egészíteném ki, hogy madártávlatból nézve
a Levene-teszt tulajdonképpen egy egytényezős variancia analízis, de ezt nem az adatpontok konkrét értékeire, hanem az adatpontoknak az átlagoktól mért távolságainak felhasználásával végezzük el.
A Levene-tesztről azt állítják, hogy hasonlít a Bartlett-tesztre, amely véleményem szerint részben igaz, részben nem. Tulajdonképpen mindkét teszt esetében az összegzett varianciát hasonlítjuk a csoport varianciák összegéhez, viszont a statisztikai próba alapmódszere teljesen más. A Levene-teszt előnye a Bartlett-teszttel szemben az, hogy kevésbé érzékeny a sokaság normál eloszlástól való eltéréseire, különösen akkor, ha az átlag helyett a mediánt vagy a csonkolt átlagot használjuk (Adathalmazok középértékének mérőszámai). A Levene-tesztcsalád tagja tulajdonképpen pont ebben különböznek egymástól, mármint abban, hogy középértékként milyen mérőszámot használnak. A medián alkalmazása az átlag helyett mindenképpen robusztusabbá teszi a tesztet aszimmetrikus eloszlású sokaságok esetén. Azt a változatot, amikor a mediánt használjuk az átlag helyett Brown-Forsythe tesztnek is nevezik a kitalálóik után.
R-ben a Levene-teszt elvégzése hasonlóan egyszerű, mint a Bartlett-teszt. Természetesen létezik egy ‘levene.test()’ függvény, amelyet megfelelő paraméterekkel meghívva a Bartlett-teszthez hasonló eredményt kapunk. Itt viszont már nem ússzuk meg, hogy ne kelljen betölteni egy csomagot, a ‘leveneTest()’ függvény a ‘car’ csomag része. Erről a csomagról nem tudok semmi különlegeset mondani, igazából biostatisztikában, közgazdaságtanban és a törvénykezésben gyakran alkalmazott módszereket tartalmaz. Egy apró könnyítés azonban lehetséges ezzel a betöltéssel kapcsolatban. Ha egyetlenegyszer lefuttatjuk az
install.package(“car”)
parancsot és a csomag sikeresen feltelepül a gépünkön lévő RStudio-ba, akkor nem szükséges minden egyes esetben előre beírni a
library(car)
parancsot. A függvényt a következő formában is meg lehet hivatkozni.
car∷leveneTest(…)
Akkor most nézzük meg, hogyan is néz ki ez a teszt a fentebb létrehozott adatokra.
#Levene's teszt a minták varianciájának összehasonlítására
car::leveneTest(adat ~ as.factor(mintaKulcs),
data = mintak2,
center = "mean")
Amint az látható, a fügvény megadása nagyon hasonlít a Bartlett-teszt függvényére. Ez esetben viszont van egy “extra” argumentum, a “center = “mean””, amely azt adja meg, hogy a Levene-teszt végrehajtása során az átlag legyen a középérték. A ‘center =’ paraméternek két különféle értéket lehet megadni. A fentebb említett “mean” esetén az átlagot, a “median” esetében pedig a mediánt fogja a függvény középértékként használni. Amennyiben a csonkolt átlagot szeretnénk középértékként alkalmazni, akkor a “center = “mean”” argumentum mellé meg kell adni a csonkolás mértékét, például a “trim = 0.1” megadással az adathalmaz két szélén lévő 5-5%-ot fogja levágni a függvény.
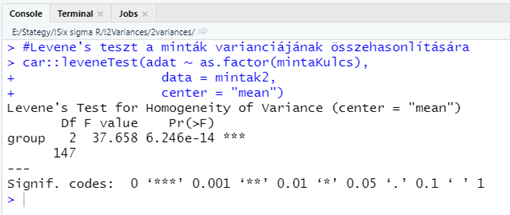
A végeredmény egy kicsit kuszább lett a megszokottnál, de azért a fő információk felismerhetők. Mondjuk, ha már ez egy egytényezős variancia analzis, akkor akár az ANOVA-táblázatot is kiírathatták volna a szerzők, de ők inkább ragaszkodtak a hipotézis vizsgálatok során rendszeres alkalmazott formához. De azért nem bírták ki teljesen, mert a riport elején szereplő ‘group’ lenne a “within”, a ‘Df’ pedig a “between” szabadsági fokok száma. Ezután az ANOVA-táblázat további részeit nagyvonalúan elhanyagolták, nehogy valaki rájöjjön, hogy miről szól a teszt, majd feltűntették az ANOVA-tábla végén szereplő F-értéket (“F value”). A ‘Pr(>F)’-nek nevezett valami a más teszteknél alkalmazott ‘p-value’ vagy p-érték, amely tulajdonképpen a nullhipotézis igaz voltának valószínűségét adja meg. Az egész riportban ez az egyetlen igazán lényeges információ a számunkra, mert eszerint majdnem nulla a valószínűsége a nullhipotézis bekövetkezésének, így azt nyugodtan elvethetjük. A ‘p-value’ mögött található három csillag, ez egy úgynevezett szignifikancia-kód, amely azt akarja itt most megadni, hogy vajon milyen megbízhatósági szinten fogadható el a teszt eredménye. A riport alján van a jelmagyarázat, mely szerint
- Ha három csillag van a riport végén, akkor gyakorlatilag nulla a nullhipotézis elfogadhatóságának valószínűsége.
- Kettő csillag esetén a nullhipotézis 99,9%-os megbízhatósági szinten utasítható el.
- Egy csillag esetén 99% százalékos valószínűséggel utasítható el a nullhipotézis.
- Egy pont esetén 95%-os valószínűséggel utasítható el a nullhipotézis
- Ha nincs a teszteredmény mögött semmilyen jel, akkor a nullhipotézist nem tudjuk elutasítani.
Most próbáljuk ki, hogy mi történik akkor, ha az átlag helyett a mediánt alkalmazzuk középértékként.
#Brown-Forsythe teszt (Levene's teszt a medián alkalmazásával)
car::leveneTest(adat ~ as.factor(mintaKulcs),
data = mintak2,
center = "median")
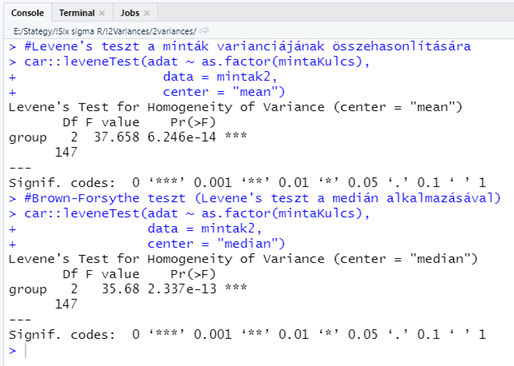
A kétféle teszt eredménye ez esetben szinte ugyanaz lett. Mivel a mintákat egy normál eloszlású sokaságból vettem ki, ezért ez az eredmény nem meglepő, hiszen a normál eloszlású adatok átlaga és mediánja közel azonos. Ha a mintákat mondjuk egy Khí-négyzet vagy egy exponenciális eloszlású sokaságból vettem volna ki, amelyek erősen aszimmetrikusak, akkor nagyobb lenne a különbség a két teszt eredménye között.
Összegzés:
A cikk megírása nehezebb volt, mint vártam. Egyrészt többféle módszerrel is megismerkedtem, amelyeknek az értelmezése nem volt egyszerű, mert a szakirodalom és az interneten lévő cikkek nagy része is csak az alap képleteket ismerteti, de azt nem, hogy ezek a képletek hogyan alakultak így. A likelihood ratio teszt leírásai számomra kínai nyelven voltak megfogalmazva. Ezzel együtt végül sikerült alaposan kitárgyalni a témakört, bár néhány teszt azért még kimaradt a szórásból. Adós maradtam többek között a Wald-teszt programjával is, illetve azzal is, hogy a Levene-tesztet elkészítsem egytényezős variancia analízisként is, amelyek külön-külön is megérnének egy-egy cikket. A legnagyobb hiányérzetem a kettőnél több mintát vizsgáló tesztekkel kapcsolatban az, hogy nem találtam olyan módszert, amellyel meg tudnám állapítani, hogy melyik minta vagy minták varianciája különbözik a többiekétől. Erre egyenlőre marad a boxplot, amelyre szeretnék majd egy számomra nagyon informatív változatot bemutatni a közeli jövőben.
Források:
Compare Multiple Sample Variances in R – STDHA (Statistical tools for high-throughput data analysis)
http://www.sthda.com/english/wiki/compare-multiple-sample-variances-in-r
Craig S Wright: Testing Homogeneity of Variance
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2953900
Wikipedia – The F-distribution
https://en.wikipedia.org/wiki/F-distribution
David Allingham: A Nonparametric Two-Sample Wald Test of Equality of Variances
https://www.hindawi.com/journals/ads/2011/748580/
Wikipedia – Bartlett’s test
https://en.wikipedia.org/wiki/Bartlett%27s_test
R-documentation – bartlett.test function
https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/bartlett.test
Wikipedia – Likelihood ratio test
https://en.wikipedia.org/wiki/Likelihood-ratio_test
StatQuest: Probability vs Likelihood
https://www.youtube.com/watch?v=pYxNSUDSFH4
David W. Nordstokke and Bruno D. Zumbo: A Cautionary Tale About Levene’s Tests for Equal Variances, University of British Columbia
https://files.eraic.ed.gov/fulltext/EJ809430.pdf
Wikipedia – Levene’s test
https://en.wikipedia.org/wiki/Levene%27s_test
R-documentation – leveneTest function
https://www.rdocumentation.org/packages/car/versions/3.0-10/topics/leveneTest
R-documentation – car package
https://www.rdocumentation.org/packages/car/versions/3.0-10
Constance Mara, Robert A. Cribbie: Equivalence of Population Variances: Synchronizing the Objective and Analysis,
https://yorkspace.library.yorku.ca/xmlui/bitstream/handle/10315/33151/equiv_based_hov_tests_mara_cribbie_jxe.pdf?sequence=1





