Ez a cikk azért kapta ezt a címet, mert két dolgot szeretnék egyszerre bemutatni:

• Az egyik, hogy hogyan lehet elkészíteni egy egytényezős varianciaanalízist (Emeljük új szintre a t-próbát - az egytényezős varianciaanalízis (oneway-ANOVA)) - R-ben,
• a másik pedig, hogy szeretném bebizonyítani, hogy az adathalmazok varianciáinak összehasonlítására szolgáló Levene’s teszt tényleg egy egytényezős varianciaanalízis (Egyformán szórnak? – Adathalmazok varianciáinak összehasonlítása R-ben), csak álcázva van.

Ez azt jelenti, hogy készíteni fogok egy több mintából álló adatsort, elvégzem rajta a Levene’s tesztet úgy, mint egytényezős varianciaanalízist, majd összehasonlítom az eredményeket a Levene’s teszt eredményeivel. Igazából teljesen mindegy lenne, hogy melyik Levene’s tesztet választom ki az összehasonlítás tárgyául. Önkényesen a Brown-Forsythe tesztet választottam, amikor a mediánt alkalmazzuk középértékként. Egy ok mindenképpen emellett szól, mégpedig az, hogy a minták nem feltétlenül lesznek normál eloszlásúak, így a medián jobb becslést ad az adatsorok középértékére. Azt előre leszögezem, hogy mindegyik teszt esetében az a nullhipotézis, hogy az összes vizsgált minta varianciája megegyezik, az ellenhipotézis pedig az, hogy a minták közül legalább egynek különbözik a varianciája a többitől.

Először is létrehozok öt darab mintát. Amint az látható, az öt minta több dologban is különbözik. A legfurább a ’minta3’ nevű, amelyet a ’minta2’ alapján készítettem, mert azt szerettem volna, hogy a minta ne balra, hanem jobbra dőljön, és a varianciája egy kicsit különbözzön a ’minta2’-étől.

A következő lépésben mindegyik mintának kiszámolom a mediánját, mert erre szükség lesz ahhoz, hogy ki tudjam számolni a minták elemeinek távolságát ezektől.

Ezután létrehoztam öt másik vektort, amelyek az egyes mintaelemeknek a minták saját mediánjától való eltérését tartalmazzák. Szerencsére R-ben ez könnyen megy.

Mivel a mintákat és a mintaelemek medián eltéréseit is szeretném megmutatni egy-egy dobozdiagramon, ezért mind a ’minta1’ – ’minta5’, mind pedig a ’mintaDev1’ – ’mintaDev5’ vektorokból készíteni fogok egy-egy adattáblát. Az ’m0’ adattábla tartalmazza az eredeti mintákat, az ’m1’ adattábla pedig a mintaelemek medián eltéréseit.

Az adattáblákat ezután úgy fogom átalakítani, hogy egy oszlopba kerüljenek a mintaelemek (’ertek’ oszlop), és egy másikba az, hogy melyik mintaelem melyik mintához tartozik (’mintaKulcs’ oszlop). A ’mintak0’ adattábla tartalmazza az eredeti mintákat, míg a ’mintak1’ adattáblában a mintaelemek medián eltérései találhatók.

Ezután még két mediánt kell kiszámolni, a ’mintak0’ és a ’mintak1’ adattáblák összes adata alapján számolt két medián értékét. Ezek nem szükségesek a konkrét vizsgálatokhoz, csupán a diagramokra szeretném vízszintesen behúzni a két adattábla fő mediánját, hogy látni lehessen, melyik mintamedián körülbelül mennyivel tér el.

Végül a fenti adattáblák és változók segítségével kirajzoltam a két dobozdiagramot. A diagramok megrajzolásához szükség van két csomagra, a ’ggplot2’-re és a ’gridExtra’ nevűre azért, hogy a két diagramot egymás mellé tudjam tenni. Itt ezeket itt hívtam meg, az eredeti R-kódban ezeket praktikus okok miatt rögtön az elején betöltöttem.

Ez esetben a ’ggplot()’ függvény argumentumaiként adtam meg a használandó adattáblákat (’data = mintak0’ a plot1, illetve data = mintak1’). A „mapping = aes(x = mintaKulcs, y = ertek))” argumentum azt adja meg, hogy a diagram x-tengelyén a minták azonosítói, az y-tengelyen pedig a minták értékei szerepeljenek. A ’geom_boxplot()’ függvény esetében megváltoztattam a kieső pontok jelölésének alakját (outlier.shape) és méretét (outler.size), hogy elüssenek az adatokat reprezentáló pontoktól. A ’geom_jitter()’ az adatpontokat ábrázolja egy kicsit szétszórva, így kaphatunk egyfajta benyomást az adatpontok elhelyezkedéséről. Itt beállítottam a pontok méretét (size), a színét (color) és az áttetszőségét (alpha), hogy a pontok ne takarják el teljesen a dobozdiagramokat. A ’geom_hline()’ egy vízszintes vonalat rajzol a diagramra. Az ’yintercept =’ paraméterrel azt lehet megadni, hogy a vízszintes vonal hol metssze el az y-tengelyt. A ’linetype = ’ paraméterrel pedig azt tudjuk megadni, hogy milyen legyen a vonal stílusa, a „dashed” a szaggatott vonalat jelöli, a „dotted” a pontvonalat, és így tovább. A ’labs()’ függvénnyel címkéket tudunk elhelyezni a diagramon, ennek a függvénynek a lehetőségeiről akár egy hosszabb lélegzetű művet is lehetne írni. Ez esetben a diagramok címeit írattam ki ezzel a függvénnyel, amelyeket a „title = ’ paraméterrel adtam meg. A diagramcímek az alapbeállításokkal túl kicsik voltak, nem lehetett őket elolvasni. A ’ggplot2’ felépítése miatt ezt nem a ’labs()’ függvényen belül kell megadni, hanem a diagram témáját (theme) tudjuk módosítani. A ’theme()’ függvény alkalmazásával a diagram megjelenésével kapcsolatos rengeteg dolgot tudunk módosítani, de ez megint csak meghaladja a cikk kereteit. A kód utolsó sorában a két diagramot (plot1 és plot2) elhelyeztem egymás mellett a ’grid.arrange()’ függvény segítségével. Az ’ncol = 2’ (number of columns) argumentum használatával azt adtam meg, hogy a két diagram egymás mellett legyen.

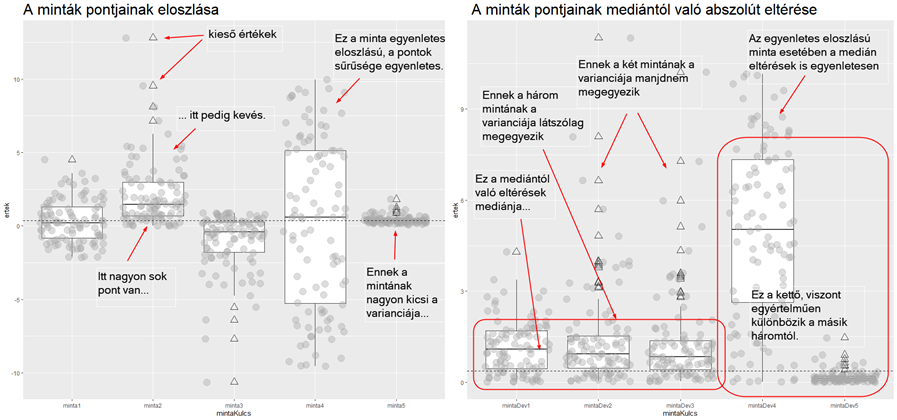
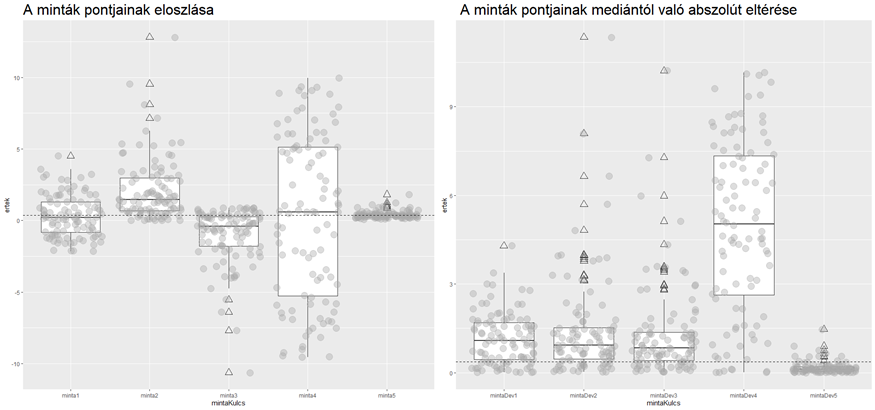
Az elkészült diagramok szemléletesen mutatják be az eredeti mintákat, illetve az ezek elemeinek medián távolságából képzett adatok elhelyezkedését. Természetesen a megjegyzéseket már utólag helyeztem el a diagramokon, hogy kiemeljek egy-két fontos részletet, amelyeket érdemes megfigyelni. Az adatpontokat ábrázoló pontdiagramok egészen sokat elárulnak a minták adatainak eloszlásáról, a dobozdiagramok pedig megmutatják a minták mediánjait és quartiliseit (Quartilisek – szeleteljük fel az adatsort!). Az összes adatpont alapján számolt medián pedig segít abban, hogy meg tudjuk ítélni, melyik adatsor mediánja mennyire tér el az összegzett mediántól. Ami mindenképpen érdekes, hogy az eredeti minták mediánjai nagyjából egybeesnek, viszont a bal oldali diagramon az is látszik, hogy a minták varianciái között viszont jelentős eltérések vannak. A baloldali ábrán a második és a harmadik minta olyan, mintha egymás tükörképei lennének, amely nem is meglepő, hiszen a harmadik minta majdnem a második tükörképe. A jobboldali ábrán ezek viszont majdnem egyformák, mert a pontok abszolút eltérései kerültek ábrázolásra. A jobboldali diagramon, ami a minták elemeinek medián eltéréseit ábrázolja, ezek az eltérések már szemléletesen kirajzolódnak. Az első három minta medián eltérései közel megegyeznek szemben a negyedik és az ötödik mintával. Vagyis a vizsgált adatok grafikus ábrázolásából ez esetben már megbízható következtetéseket tudunk leszűrni az adatokkal kapcsolatban.

A célom viszont nem ez, hanem az egytényezős varianciaanalízis és a Levene-teszt összehasonlítása. A bizonyítandó állítás ezek szerint az, hogy ha ugyanarra az adatsorra alkalmazzuk az egytényezős varianciaanalízist és a Levene-tesztet, akkor ugyanazt az eredményt fogjuk-e kapni. A teszthez először a fentebb már létrehozott ’mintak1’ adattáblát fogom használni. Nézzük először az egytényezős ANOVA-t.

A varianciaanalízis végrehajtásához R-ben az ’aov()’ függvényt tudjuk meghívni. Ez egy kétlépcsős folyamat első eleme. Az ’aov()’ függvény elkészít egy adatbázist, amely az ANOVA-vizsgálat eredményeit tartalmazza, de önmagában nem ír ki semmit. Az ANOVA-táblázat elkészítéséhez a ’summary()’ nevű függvényt tudjuk alkalmazni, ez ugyanazt az egytényezős ANOVA-táblázatot rajzolja ki, amelyet már korábbról jól ismerünk (Egy kis sörhabológia – Példa egytényezős varianciaanalízisre (One-way ANOVA)).

Alá pedig oda szeretném tenni a Levene-teszt eredményét ugyanarra az adatsorra, azaz a minták medián eltéréseire.

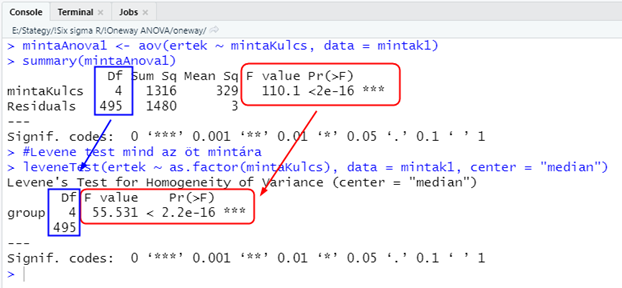
A két riportot egymás alá helyezve még jobban kitűnik, hogy a szabadsági fokok számát valamiért gondosan feltüntették a Levene-teszt eredményei között is, bár szerintem ez esetben ennek annyi csak a jelentősége, hogy mi alapján számolták ki a teszt kritikus határértékét, amelyet általában gondosan kifelejtenek minden teszt eredményből. Nagy csalódásomra a tesztek F-értékei nem egyeznek meg, sőt lényeges eltérés van közöttük. Ennek oka lehet a két teszt elkészítése közötti eltérés is, de az is, ahogyan az adatokat elő kell készíteni, ami lehet az én hibám is. Ennek a témának eléggé szűkös a szakirodalma, én pedig lehet, hogy félreértettem valamit. A talált cikk így fogalmaz:

„… In order to assess variance homogeneity, Levene (1960) proposed transforming the sample scores to the absolute deviations of the sample scores from the sample mean with zij = |Xij – Mj| where Xij is the score of the ith individual in the jth group and Mj is the mean of the jth group, and then using a traditional ANOVA F-test on the zij to assess variance equality across groups. …”

Szóval szerintem jól csináltam mindent. A kapott p-értékek viszont eléggé egyformának tűnnek, de ez lehet amiatt is, mert abban az eloszlástartományban már nagyon kicsi valószínűségekről beszélgetünk.

Azért, hogy megnézzük, hogyan működik a két teszt akkor, ha a minták varianciái megegyeznek. Ehhez létrehoztam egy olyan adattáblát, amelyben csak az első három minta szerepel. ezt úgy tettem meg, hogy a ’tidyR’ csomagban található ’filter()’ függvény alkalmaztam egy az R programozási nyelvre jellemző formában.

Ez a kód most ismét részletesebb magyarázatra szorul, mert jónéhány dolog eléggé kínainak tűnik. Az elsősorban van a ’mintak1’ adattábla, ebből szeretnénk kiszűrni az első három minta adatait. Ezután van egy fura ’%>%’ jelsorozat. Ezt az R-ben ’pipe’-nak (magyarul gondolom „pipának”) nevezik és ennek az a jelentése, hogy a … felhasználva tegyél meg …, vagyis az első sor jelentése körülbelül az, hogy a ’mintak1’ adattáblát felhasználva tegyél meg valamit. Az, hogy mit, a második sorban derül ki, amikor a ’filter()’ függvény kerül képbe, azaz a mondat valahogy úgy néz ki, hogy a ’minták1’ adattáblából szűrj ki sorokat, amelyek megfelelnek bizonyos feltételeknek. Ez a feltétel került be a ’filter()’ függvény zárójelei közé. Ez egy összetett feltétel, amelyet egy sorba is lehetne írni, azért írtam három sorba, hogy jobban elférjen. A feltétel jelentése körülbelül annyi, hogy a ’mintak1’ adattáblából legyenek kiválasztva mindazok a sorok, amelyek esetében a ’mintaKulcs’ mező értéke ’mintaDev1’, ’mintaDev2’ vagy ’mintaDev3’. A kettős egyenlőségjel (’==’) az R-ben az egyezőséget jelző szimbólum, a függőleges vonal (’|’) pedig a „vagy” logikai döntés jele. A legvégén egy másik „pipe” található, amely egy nyilat formáz. Ez azt mondja, hogy a ’mintak1’ adattáblából a fenti feltételek alapján kiszűrt sorokat helyezze el az R a ’mintak2’ adattáblában. Ennek hatására létrejön a ’minták2’ adattábla 300 sorral (a ’mintak1’ adattábla 500 soros volt, mert 5 x 100 mintát hoztam létre az elején. Vagyis a fenti kód tulajdonképpen olyan, mint egy mondat.

A ’mintak1’ adattáblából válaszd ki azokat a sorokat, amely esetében a mintaKulcs mező értéke ’mintaDev1’, mintaDev2’ vagy ’mintaDev3’ és másold ezeket a sorokat a ’mintak2’ adattáblába!

Ez a fajta programozási nyelvezet nagyon érthetővé teszi a kódot. Így is meg kell tanulni egy csomó dolgot, de utána jelentősen leegyszerűsödik a szkript megírása és utólagos értelmezése is. És most nézzük az egytényezős varianciaanalízist és a Levene-tesztet, ezúttal az újonnan létrehozott adattábla adataival.

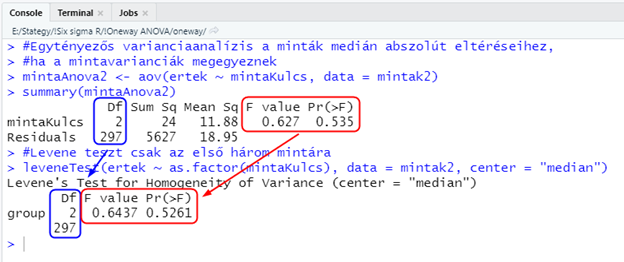
Az eredmények hasonlóak a korábbihoz. Ez alkalommal mind az F-próba statisztika értéke, mind pedig a p-érték közel megegyezik, szóval annyira nagy hibát nem követhettem el, a korábban tapasztalt eltérésnek talán nem számolási hiba az oka, hanem valami más.

Az egytényezős varianciaanalízis alkalmazása a Levene-teszt helyett akkor lehet praktikus, ha nemcsak arra vagyunk kíváncsiak, hogy a minták varianciái megegyeznek-e vagy sem, hanem arra is, hogy melyik minták lógnak ki a sorból. A Levene-teszt esetében nincs konyhakész megoldásunk, hiszen a minták varianciáit és nem az átlagait vizsgáljuk. Az egytényezős ANOVA esetében viszont több lehetőségünk is van a minták további elemzésére, úgyhogy véleményem szerint legalábbis érdemes megemlíteni, hogy ezek a lehetőségek a minták varianciáinak eltérése esetén is alkalmazhatók, ha az adatokat a fenti módon átalakítjuk.

Ilyen például a Tukey-féle páros összehasonlítás, amelyet R-ben is tudunk alkalmazni a minták elemeinek abszolút medián eltéréseire. Ez a teszt minden lehetséges mintapár esetében összehasonlítja a minták átlagainak távolságát és az átlagok különbségeihez tartozó megbízhatósági tartományokat, a minták darabszámai alapján kiválasztott student-eloszlások alapján. Ezután azt vizsgálja, hogy a minták megbízhatósági tartományai alapján a különbség lehet-e nulla, vagy sem.

A fenti riportban felül az öt minta összehasonlítása látható. A táblázat ’diff’ oszlopa a két mintaátlag különbségét adja meg, a ’lwr’ és az ’upr’ oszlopokban találhatók a különbségre kiszámított megbízhatósági határok. Ha mindkét szám pozitív, vagy mindkét szám negatív, akkor a két átlag különbsége nem lehet nulla, ez esetben a ’p adj’ oszlopban található szám nagy valószínűséggel kisebb lesz, mint 0,05. Ellenkező esetben, ha az egyik szám pozitív, a másik negatív, akkor a különbségük lehet nulla.

Az öt minta vizsgálatakor az jött ki, hogy csak a negyedik minta varianciája lóg ki a sorból. Ez azért fura, mert a dobozdiagram alapján azt gondoltam volna, hogy az ötödik minta varianciája sem egyezik meg az első hároméval. A három minta összehasonlítása esetében mindhárom minta különbsége lehet nulla, így nem bizonyítható, hogy a minták varianciái eltérnek.

Egy másik lehetőség a mintaátlagok páros összehasonlítása kétmintás t-próbák alkalmazásával. A kétmintás t-próbát már korábban részletesen bemutattam (Minden „sikeres” minta mögött áll egy sokaság – Kétmintás t-próba R-ben), így erre most külön nem térek ki. Ezt a ’pairwise_t_test()’ függvény segítségével tudjuk könnyen elvégezni. Itt felhívom a figyelmet, hogy a függvény nevében aláhúzás karakterek és nem pontok vannak. Létezik a ’pairwise.t.test()’ függvény is, és az általam alkalmazott aláhúzásos változat is ezt hívja meg, de az aláhúzásos verzió működik a fentebb már alkalmazott újszerű programnyelvvel is.

A fenti kódsorban egyetlen újdonság van a korábbiakhoz képest, a „pool.sd = FALSE” azt jelenti, hogy a t-próbák alkalmazásakor a Welch-próbát alkalmazza a függvény.

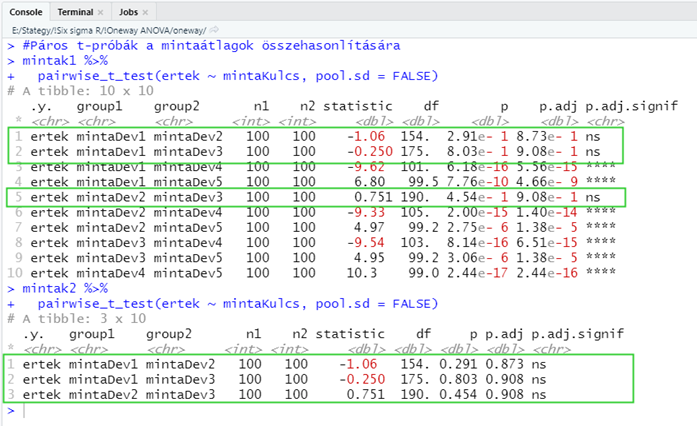
Az eredmény a Tukey’s páros összehasonlításhoz hasonló táblázat. Az ’n1’ és az ’n2’ oszlopokban vannak a minták elemszámai, a ’statistics’ oszlop a t-próba statisztika eredménye, a ’p’ oszlopban vannak a t-próbák p-értékei, a ’p.adj’ oszlopban a korrigált p-értékek szerepelnek (erről még majd kell írnom). A p.adj.signif’ oszlopban pedig az, hogy a teszt milyen megbízhatósági szinten fogadható el.

ns: no significance (nullhipotézist elfogadjuk)

 *: 0,05 significance (a nullhipotézist 95%-os megbízhatósági szinten elutasítjuk)

**: 0,01 significance (a nullhipotézist 99%-os megbízhatósági szinten elutasítjuk)

***: 0,001 significance (a nullhipotézist 99,9%-os megbízhatósági szinten elutasítjuk)

****: 0 significance (a nullhipotézist mindenképpen elutasítjuk)

Úgy tűnik, hogy ez a teszt érzékenyebb, mint a Tukey’s páros összehasonlítás, ez esetben a teszt eredménye az lett, amire már a dobozdiagram is utalt, vagyis az első három minta varianciája egyezik meg, a többié mind különbözik. Az első három minta vizsgálata az ennek megfelelően várható eredményt hozta.

Végül két ideillő diagramot szeretnék bemutatni, így teljessé téve a történetet. Mindkét diagramot a ’plot()’ nevű függvény segítségével tudom megjeleníteni. Az első diagram az úgynevezett residuals vs. fitted diagram, a másik pedig a residuals (maradékok) eloszlását mutatja meg. Ehhez a két diagramtípushoz megint csak kell egy kicsivel több magyarázat.

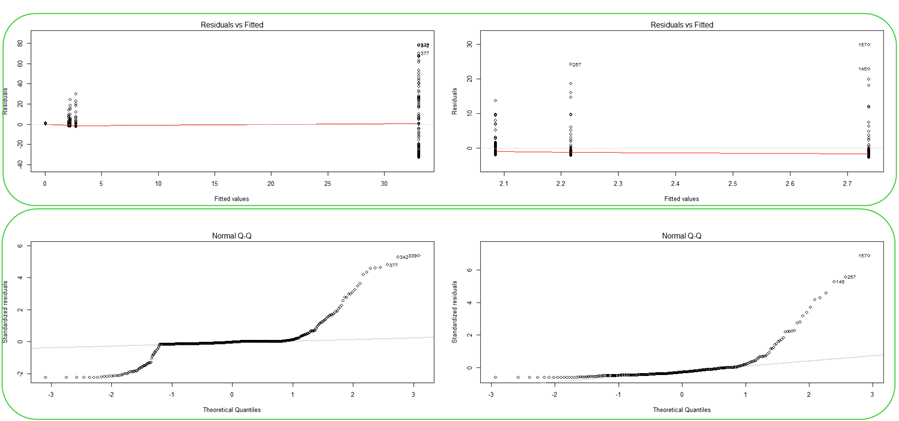
A residuals vs. fitted diagram azt mutatja be, hogy az egyes minták esetében hogyan szóródnak a pontok a középértékhez képest. Ne felejtsük el, hogy ez esetben nem a minták középértékéről, hanem a minták medián abszolút eltéréséről beszélünk, ezeknek az átlaga pedig tulajdonképpen a minta varianciája (egy kicsit másként, mert nem az eltérések négyzetéből vonunk gyököt, hanem a pontok átlagtól való eltérésének abszolút értékét vesszük, lásd Adathalmazok középértékének mérőszámai).

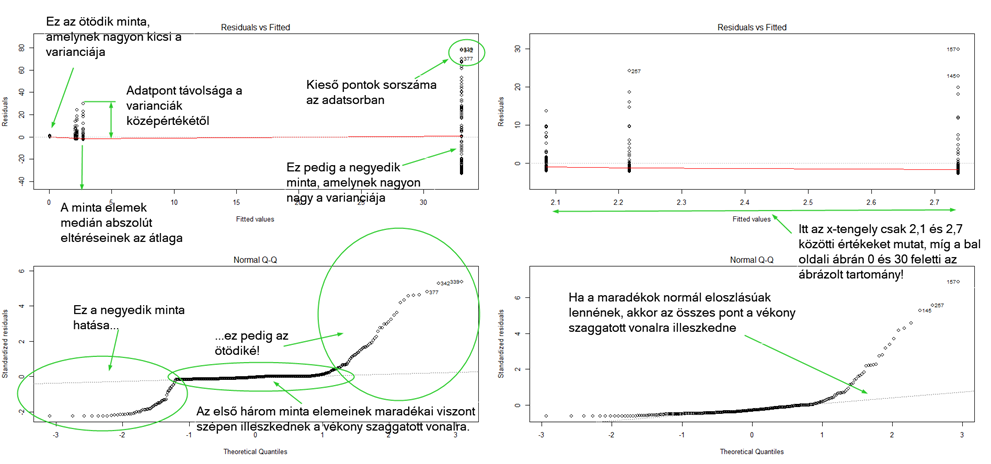
A második diagramtípus azt mutatja meg, hogy a vizsgált minták esetében a maradékok (residuals) eloszlása normál eloszlást mutat-e. Ez azért fontos, mert amikor a minták azonos normál eloszlású sokaságból származnak, akkor azt várjuk, hogy a pontok (jelen esetben a pontok medián eltérésének különbsége a medián eltérések középértékétől) különbsége a középértéktől normál eloszlást mutat. Ez a feltétel még a három – egyébként egyforma varianciájú – minta esetében sem teljesül, valószínűleg amiatt, mert a második és a harmadik minta eloszlása sem normál eloszlású. Ez a tény rámutat az egész cikk legnagyobb problémájára. Mivel az eredeti minták nem normál eloszlásúak, ráadásul nem is ezeket, hanem ezek abszolút medián eltéréseit vizsgáltuk, ezért várható volt, hogy a maradékok nem lesznek normál eloszlásúak.

Összegzés:

A hosszú levezetés során sikerült bizonyítani, hogy a Levene-teszt tulajdonképpen egy speciális egytényezős varianciaanalízis, illetve azt is sikerült megmutatni, hogyan kell egy egytényezős varianciaanalízist elkészíteni R-ben. Ez azt is jelenti egyben, hogy bizonyos esetekben előnyösebb lehet, ha a vizsgált minták varianciáit ilyen módon összehasonlítani, mert ez esetben további elemzésekkel meg tudjuk határozni melyik minták varianciái térnek el a többiekétől.

Források:

Introduction to R - Data Wrangling with Tidyverse
https://hbctraining.github.io/Intro-to-R/lessons/08_intro_tidyverse.html

STDHA - One-Way ANOVA Test in R
http://www.sthda.com/english/wiki/one-way-anova-test-in-r

StackExchange Cross Validated - Residual Analysis and ANOVA Model
https://stats.stackexchange.com/questions/211379/residual-analysis-and-anova-model

Constance Mara, Robert A. Cribbie: Equivalence of Population Variances: Synchronizing the Objective and Analysis,
https://yorkspace.library.yorku.ca/xmlui/bitstream/handle/10315/33151/equiv_based_hov_tests_mara_cribbie_jxe.pdf?sequence=1

RDocumentation – TukeyHSD function
https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/TukeyHSD

 rdrr.io - pairwise_t_test: Pairwise T Tests
https://rdrr.io/github/pstraforelli/tidytests/man/pairwise_t_test.html