
Azt hiszem egyetlen sörkedvelőnek sem kell elmagyarázni, hogy egy jó sör élvezeti értékét – sok más tényező mellett – a sörhab különféle jellemzői adják. A mezei sörfogyasztó számára – mint amilyen én is vagyok – a sörhab minősége nem objektív fogalom. Nem tudom megmondani, hogy mitől jó a sör habja, maximum azt tudom eldönteni, hogy az egyik sör habja jobb, mint a másiké. Mivel nem is célom, hogy a tökéletes sörhab készítésének rejtelmeit feszegessem, ha érdekel a témának ez a része, akkor nézd meg ezt a blogbejegyzést:
Amit ehelyett feszegetni szeretnék, az a sörhab minőségének objektív mérése, a különféle sörkészítési eljárások és receptúrák tesztelésének tudománya – és persze ezen keresztül – egy statisztikai elemzési módszer gyakorlati alkalmazásának bemutatása.
A sörhabnak szabályos „életciklusa” van, az egyes lépések megadott sorrendben követik egymást:

Természetesen a sörhabnak nagyon sokféle számszerűsíthető jellemzője van, de az egyszerűség kedvéért kiragadok két, egyébként fontos jellemzőt:
Az egyik a %Tapadás (%Adhesion), ami szerintem nem egy szerencsés elnevezés, mert a jellemző azt mutatja meg, hogy a kitöltés utáni másodpercekben mennyire marad meg a sörhab magassága.
A másik pedig az %Összeesés (%Collapse), ami azt mutatja meg, hogy a sör mennyire esik össze a sörhab koronájának felépülése után.
A jellemzők és a teszt leírása nem mai történet, a felhasznált tanulmány 1967-ben íródott, vagyis azóta a sörhabok tesztelése és értékelése is sokat fejlődött.
A tanulmány nagy előnye viszont az, hogy szabadon hozzáférhető, illetve a mérési adatokat is tartalmazza, vagyis rendelkezésre áll egy olyan nyers mérési adatsor, amelyet fel lehet dolgozni. A tanulmány bemutatja a sörhab mérésének egy szofisztikáltabb módját, amely ismételhetővé teszi a mérést. Az alapprobléma az, hogy a sör kiöntésének módja nagymértékben befolyásolja a sörhabban keletkező buborékok számát és méretét, amely viszont a hab stabilitását befolyásolja lényegesen. Ez a szóródás akadályozza a különféle receptúrák hatásának összehasonlítását a habképződés tekintetében.
A tanulmányban ismertetett mérési eljárás lényege, hogy a sört nem kiöntik, hanem a fix mennyiségű (100 ml) mintába szabályozott körülmények között szintén fix mennyiségű és nyomású széndioxidot fecskendeznek egy egyszerű fojtáson keresztül. Ennek hatására a sör felkerül a mérőhengerbe, amelynek skálázott oldalán le lehet olvasni a vonatkozó értékeket a vizsgálat közben. A mérés részletes leírását nem szeretném itt közölni, akit érdekel, a fent említett tanulmányban ez részletesen ismertetésre került.
A mérés összeállítás a következő módon néz ki:
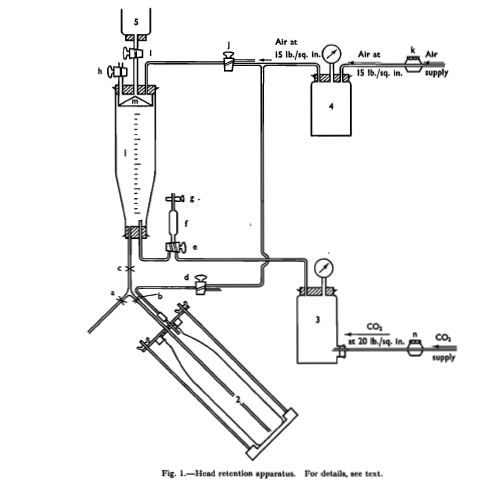
A mérés kiértékelése a következő módon történik:
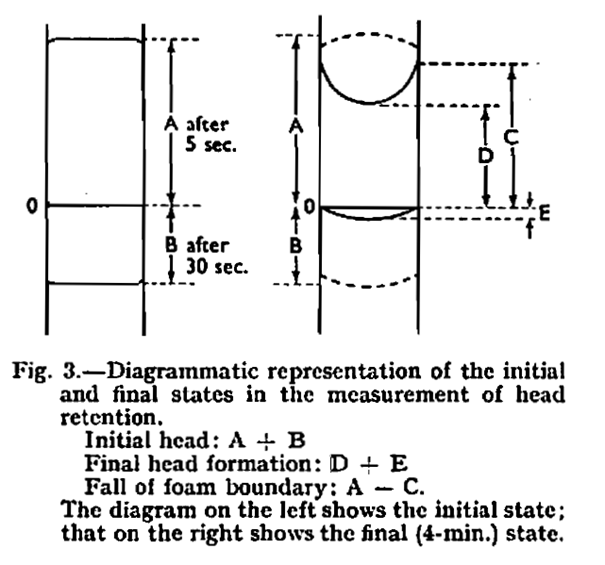
- A mérés megkezdése után 5 másodperccel le kell olvasni a sörhab magasságát a 0 értéke felett, ez lesz az A érték.
- A kezdés után 30 másodperccel újra le kell olvasni a maradék hab magasságát a 0 érték alatt, ez lesz a B érték.
- A mérés megkezdése után 240 másodperccel újra le kell olvasni a maradék hab magasságát, ez lesz a C érték
- A habkorona közepének magassága 240 másodperc után lesz a D érték
- A maradék sör magassága lesz az E érték.
A keresett két jellemző a következő módon adódik:

Ez alapján a %Tapadás tulajdonképpen azt mondja meg, hogy a kezdeti habkorona magassághoz képest hány százalékkal esik össze a hab 4 percen belül a „pohár” falán mérve, a %Összeesés pedig a habkorona közepének százalékos csökkenését méri.
A lényeg, hogy a mérés azonos tétel többszöri vizsgálatakor nagyon pontosan ismétli önmagát, így az egyes receptúrák közötti kis különbségeket is képes a vizsgálat kimutatni.
A tanulmányban megmérték három sörösrekesz összes palackját és feljegyezték a mérések eredményeit. Csak megjegyzésként, a „Max. head formation” jellemző a sörhab jellemzőit magyarázó kép alatt található „Initial head formation” jellemzővel egyezik meg, azaz a tesz megkezdése után 5 másodperccel és 30 másodperccel az üvegedény falán mért sörhabmagasságok különbsége.
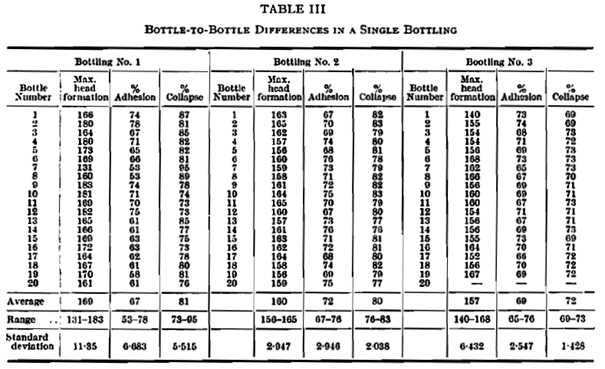
Ezt a táblázatot begépeltem, és most azt tervezem, hogy kézzel végig számolom az ANOVA-táblát, ahogyan azt a korábbi vonatkozó bejegyzéseben is megtettem (Emeljük új szintre a t-próbát - az egytényezős varianciaanalízis (One-way ANOVA)). Megtehetném, hogy csak Minitab-bal dolgozom fel az adatsort, de akit tényleg érdekel, annak talán többet segít a részletes számítás ismertetése, mintha csak az eredményeket mutatom meg. Mielőtt azonban belevágunk, nézzük meg, hogy első blikkre hogy néznek ki az adatok. A három rekesz esetében az átlagok sorba 169, 160 és 157, a terjedelmek pedig 131-183, 150-165 és 140-168 között mozognak. Az első rekesz átlaga magasabb, mint a másik kettőé, de az adatsorok eléggé átfedik egymást. Ha grafikusan ábrázoljuk őket, akkor azt látjuk, hogy a vonaldiagramon a három adatsor nagymértékben fedi egymást, talán a kék (Rekesz #1) mintha magasabb értékeket mutatna, mint a másik kettő, de a 7-es és a 12-es adatok valószínűleg lefelé húzzák az első rekesz átlagát.
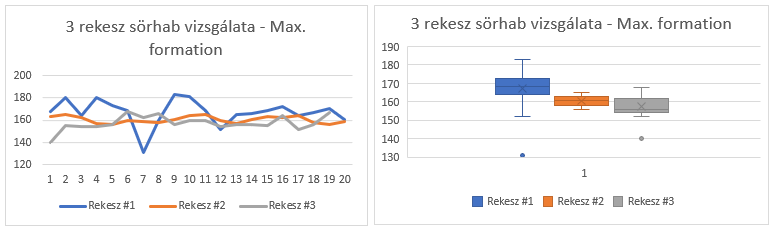
A dobozdiagram azt mutatja, hogy a az első rekesz adatainak szóródása nagyobb, mint a másik kettőé és természetesen az átlaga is nagyobb náluk. De az eddigi adatok szerintem nem perdöntőek, szóval valamilyen komolyabb döntési kritériumra van szükségünk.
Erre lesz jó az egytényezős varianciaanalízis. Az első dolog, hogy tisztázzuk, mi a nullhipotézisünk és mi az alternatív hipotézis. A nullhipotézis az, hogy a három adatsor ugyanabból a sokaságból származik, vagyis az átlagaik között nincs lényeges eltérés. Az alternatív hipotézis pedig azt mondja, hogy a három adatsor közül legalább az egyik különbözik a többitől. A döntésünket 95%-os megbízhatósággal szeretnénk meghozni.
Akkor lássunk hozzá:
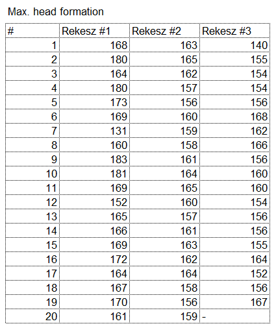
Mivel a különböző jellemzőket külön-külön dolgozom fel, ezért az egyes jellemzők adatait egymás mellé másoltam a jobb áttekinthetőség kedvéért. Úgy tűnik, hogy a harmadik rekeszből eggyel kevesebb üveget vizsgáltak meg a tudósok, gondolom az utolsó üveget jóízűen elfogyasztották a jól végzett munka jutalmául… �
Először is kiszámoltam a három csoport átlagát:
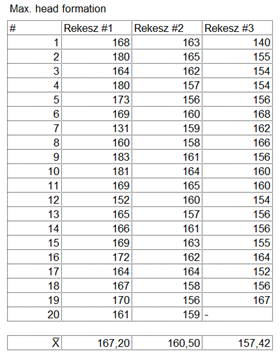
Az átlagok között van egy kisebb eltérés, de ez alapján természetesen nem vonnék le messzemenő következtetéseket… Most pedig kiszámolom a három csoport átlagának átlagát, a nagyátlagot:

Ezek után pedig az egyes csoportok átlagai és a nagyátlag közötti eltéréseket…

… majd ezek négyzetét…
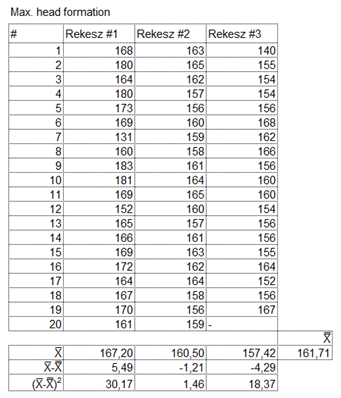
… majd a négyzetek és a csoportok elemszámainak szorzatát…
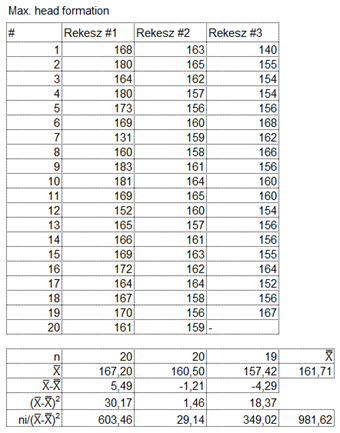
Most már elegendő kiinduló adatunk van ahhoz, hogy elkezdjük kitölteni az ANOVA táblázatot.

Kezdjük a szabadsági fokok számával. A csoportok közötti (Between) szórás szabadsági foka (df) 2, mivel 3 különböző rekeszt vizsgáltunk meg, azaz három adathalmazt hasonlítunk össze. A teljes (Total) szórás szabadsági foka pedig 58, mert összesen 59 darab adatunk van. A csoportokon belüli (Within) szórás pedig az előző két szám különbsége, azaz 58 – 2 = 56. Így a df oszlop a következő módon alakul:
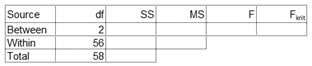
Akkor most lássuk az SS oszlopot. Az SS between értékének kiszámításához már megvan minden adatunk. Ahogy azt az előbb említett bejegyzésben részletesen elmagyaráztam, a csoportok közötti 'Sum of Squares' kiszámítása a következő módon történik:
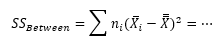
Ezt úgy kaptam meg, hogy az első sorban kiszámoltam mindhárom rekesz adatainak átagát. Ezekből kiszámoltam a nagyátlagot, azaz a három csoportátlag átlagát. A második sorban kiszámolom a három csoportátlag különbségét a nagyátlagtól. A harmadik sor tartalmazza a második sorban kiszámolt különbségek négyzetét. a negyedik sorban pedig a harmadik sorban kapott négyzetre emelt különbségeket megszorozzuk az egyes csoportok elemeinek számával. Az első két rekesz esetében 20 mérésünk van, a harmadik rekesz 19 mérést tartalmaz, azaz az első két rekesznél n értéke 20, a harmadiknál pedig 19.
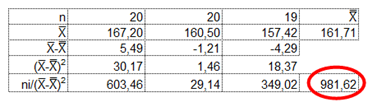
A csoportokon belüli (Within) 'Sum of Squares' értékeinek kiszámításához az egyes csoportokon belül minden egyes elemből ki kell vonni a csoportátlagot és a különbségek négyzetét kell összegezni:
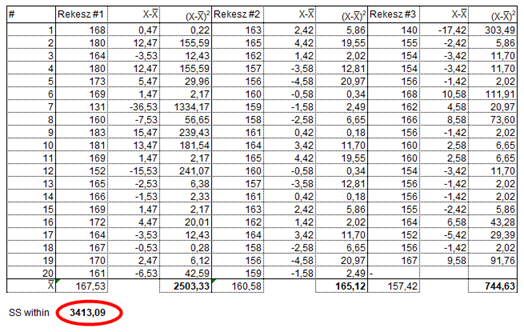
Az SS within a három csoport négyzetösszegeinek az összege. Vagyis az ANOVA-táblázatunkat újabb eredménnyel tudjuk kiegészíteni:
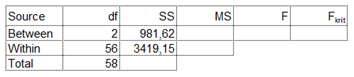
Az SS Total kiszámításához pedig a három csoport összes eleméből (mind az 59 számból) ki kell vonni az 59 szám átlagát és ezen különbségek négyzetösszegét kell kiszámítani.

Így az ANOVA-táblázatunk második oszlopa is teljes lett:
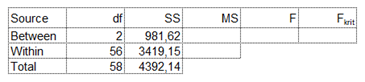
Ezután az MS between és az MS within kiszámítása már pofonegyszerű, csak el kell osztani a megfelelő SS értéket a megfelelő df-el, azaz a szabadsági fokok számával. Ezt táblázatkezelőben már az ANOVA-táblázaton belül is el tudom végezni:
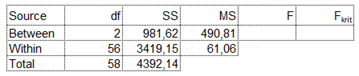
F értéke pedig a két MS érték hányadosa:

Mivel az F-eloszlás táblázatomban csak df=50-ig vannak megadva az F-eloszlás értékei, ezért az F eloszlás kritikus határértékét a táblázatkezelő beépített =F.INVERZ.JOBB(0,05; 2; 56) függvény segítségével. Ennek eredménye 3,16 lett. Az F-eloszlás táblázatomban a df1=2 és a df2=56 értékeknél 3,18 szerepel, vagyis a kapott 3,16 valószínűleg helyes.

Végre eljutottunk a döntésig. Azt látjuk a két F-értékből, hogy a próba statisztika (F = 8,04) jóval nagyobb, mint az F kritikus értéke (F krit = 3,16). Ez azt jelenti, hogy a nullhipotézist elvetjük, és az alternatív hipotézist fogadjuk el, azaz a három rekesz közül legalább egy esetében más a sörhab maximális magassága, mint a többinél.
Egy következő bejegyzésben megnézzük majd, hogy hogyan néz ki ugyanez az elemzés Minitab alkalmazásával.







