Az ismert idézet kifordítása elsőre talán nem tűnik túlzottan indokoltnak, de remélem, hogy a bejegyzés végére érthetővé válik, hogy mire is gondoltam. A kétmintás t-próbáról már írtam korábban (Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba), de abban a cikkben nem volt szó a sokaság és az abból kivett minták kapcsolatáról. Most viszont az R statisztikai program bemutatása kapcsán szeretném egy kicsit a módszert egy kicsit erről az oldalról is körbejárni a témát.

A kétmintás t-próba alapkérdése elvileg az, hogy vajon két egymástól független minta megegyezik-e. Szerintem viszont ez a próba nem erről szól, hanem arról, hogy mindkét mintát kivettük egy-egy sokaságból. Vajon igaz-e az, hogy a két sokaságból kivett egy-egy minta csak akkor egyezik meg, ha a mögöttük álló sokaságok is megegyeznek egymással? Vajon mekkora lehet annak a valószínűsége, hogy két egymástól különböző sokaságból sikerülhet kivenni egy-egy olyan mintát, amelyek megegyeznek egymással? Mennyire és milyen módon különbözhet egymástól két sokaság ahhoz, hogy a belőlük kivett minták 95%-os valószínűséggel megegyezzenek?

A példa kedvéért készítettem két egymástól különböző 10 000 elemű sokaságot, amelyeket különféle normál eloszlásokból „ollóztam” össze, majd kivettem ezekből 10 000 -10 000 darab 100 elemű mintát, végül kiszámítottam a minták átlagait. A bal oldali diagramon a két sokaság amorf vonala látszik, illetve a belőlük kivett minták átlagai. Érdekes, hogy mivel a két sokaság eloszlása eltérő, ezért a belőlük kivett nagy elemszámú minták átlagai is lényegesen különböznek. A jobb oldali diagram a mintaátlagok eloszlásait mutatja és azt, hogy milyen kicsi a két minta eloszlás közös része, azaz mennyire kicsi a valószínűsége annak, hogy a két sokaságból kivett minták átlaga megegyezik.

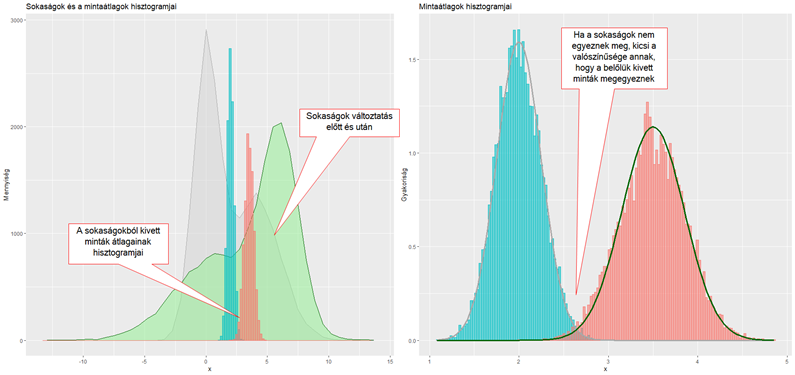
Persze a fenti állítás a valóság végletes leegyszerűsítése, hiszen a vizsgált sokaságokról sajnos nem tudunk semmit. Vagyis a kapott eredmény nagyban függ a vizsgált sokaságok átlagainak távolságától, szórásaik mértékétől és azok különbségeitől, illetve a sokaságokból kivett minták elemszámától is. Az alábbi két ábrán látható, hogy ha a sokaságokból csak ötelemű mintákat veszünk ki (felső hat diagram), akkor a mintaátlagok egy széles tartományban szóródnak, így még akkor is jelentős lehet az átfedés a két sokaság mintaátlagai között, ha a sokaságok átlagai jelentősen eltérnek

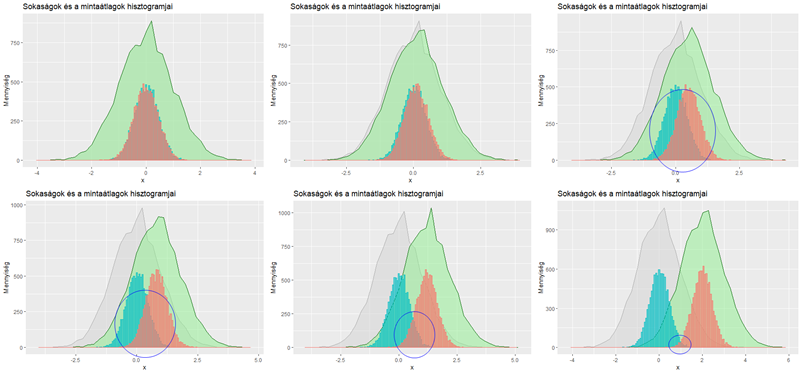
Amennyiben a sokaságokból 50 elemű mintákat veszünk ki, abban az esetben a mintaátlagok egy sokkal kisebb tartományban fognak szóródni, így a már a sokaságok átlagainak sokkal kisebb eltérése esetén is kicsi a valószínűsége annak, hogy a két kivett minta átlaga megegyezik annak ellenére, hogy a sokaságok átlaga különbözik.

A két diagram között látható eltérés még az, hogy míg a felső hat diagramon a sokaságok görbéi a magasabbak, addig az alsó hat diagram esetében a mintaátlagok hisztogramjai törnek magasabbra. Persze, mert a magasabb mintaelemszámok miatt a második esetben a mintaátlagok egy sokkal szűkebb tartományban koncentrálódnak, így középre sokkal több mintaátlag jut.

A nagy dobókocka kísérletből már megtudtuk, hogy a Centrális Határeloszlás tétele alapján a mintaátlagok átlaga megegyezik a sokaság átlagával, a mintaátlagok szórása megegyezik a sokaság szórásának és a minta elemszám négyzetgyökének hányadosával. Az egymintás t-próba esetében a próbastatisztika kiszámítására következő képletet alkalmaztuk:

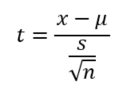
Vagyis a minta átlagából kivontuk a sokaság átlagát, majd elosztottuk az átlag standard hibájával.

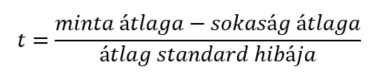
Hogy néz ez ki a kétmintás t-próba esetében?

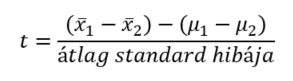
Mivel feltételezzük, hogy a két sokaság átlagának különbsége 0, hiszen ez a nullhipotézisünk, ezért a (μ1-μ2) különbség 0, vagyis ezt kivehetjük a képletből.

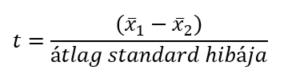
De ez esetben mi lesz az átlag standard hibája? Mivel a két sokaság szórását nem ismerjük, ezért ezeket a két minta szórásával fogjuk helyettesíteni ugyanúgy, mint az egymintás t-próba esetében (Amikor túl kevés a vizsgálandó minta…). Innentől két eset lehetséges:

• A két minta elemszáma és varianciája megegyezik, illetve
• a két minta elemszáma és/vagy varianciája jelentősen eltér egymástól.

Az első esetben egy kicsit bonyolultabb az átlag standard hibájának a kiszámítása (de azért annyira nem). Amennyiben valamilyen módon meggyőződtünk arról, hogy a két minta varianciája között nincs szignifikáns eltérés (például kétmintás F-próba alkalmazásával, amiről még lesz szó egy későbbi másik bejegyzésben), akkor a két minta varianciája alapján kiszámított – a minták elemszámaival – súlyozott átlagos szórást alkalmazzuk.

A két minta varianciájának átlaga

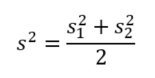
Azonban ezt a formulát nem ebben a formában alkalmazzuk, mert a következő képlet alkalmazásával olyan mintákat is tudunk vizsgálni, amelyek mintaelemszáma nem egyezik meg. Ebben az esetben viszont a varianciák átlagát súlyoznunk kell a minták elemszámával.

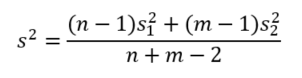
ahol

n – az első minta elemszáma,

m – a második minta elemszáma.

Ezután a fent említett átlagvariancia négyzetgyökét alkalmazzuk a t próbastatisztika kiszámításához, amely tulajdonképpen a két mintaátlag különbségének a standard hibája.

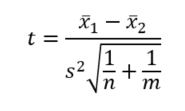
A ’tkrit’ kritikus határérték megállapításához a Student-eloszlás ν = (n + m – 2) szabadsági fokú függvényének az előre meghatározott 95% vagy 99%-os (vagy egyéb) megbízhatósági szintjéhez tartozó eloszlásértéket kell kikeresnünk táblázatból vagy kiszámolnunk táblázatkezelővel vagy valamilyen statisztikai szoftverrel.

Amikor a két minta elemszáma és/vagy varianciája jelentősen eltér egymástól, akkor viszont egy más módszerrel kell elvégeznünk a két minta átlagának összehasonlítását, ezt Welch – próbának nevezik. A próba menete hasonló a kétmintás t-próbáéhoz, de mivel ez esetben a két minta varianciája jelentős mértékben eltér egymástól, ezért nem az átlagvarianciával, hanem a két minta varianciájával számolunk.

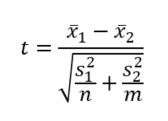
Ez így lényegesen egyszerűbbnek tűnik, mint az előzőekben ismertetett átlagos varianciával számoló képlet. Viszont ennek az árát a másik oldalon fizetjük meg, mivel a ’tkrit’ kritikus határérték kiszámításához szükséges Student-eloszlás szabadsági fokának meghatározása válik sokkal bonyolultabbá, mivel ez esetben nem a ν = (n + m – 2) szabadsági fokú t-eloszlást kell alkalmaznunk. A szabadsági fok meghatározásához a következő „egyszerű” képletet kell alkalmaznunk.

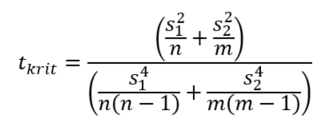
Erről most legyen elég annyit tudni, hogy amikor a két minta varianciája különbözik, akkor a szabadsági fokok megállapításakor a Welch–Satterthwaite egyenletet alkalmazzuk az effektív (hatásos) szabadsági fok meghatározására a független minta varianciák lineáris kombinációjaként (nekem ez már kínai). Akit érdekel, a források közé odatettem a Wikipédia linket…

Tehát az az első esetben a próbastatisztika, a második esetben viszont a kritikus határérték meghatározása lesz egy kicsivel bonyolultabb.

Akkor most nézzük meg, hogyan néz ez ki R-ben.

Először is létrehoztam két „sokaságot” két-két normál eloszlás kombinációjaként. Először létrehoztam a két normál eloszlású 10 000 – 10 000 elemből álló sokaságot (’sokasag11 és sokasag12) az ’rnorm()’ függvény segítségével, majd a ’sokasag1’ nevű változóba összefűztem őket. Ugyanezt tettem a ’sokasag2’ esetében.

Ezután elkészítettem a mintákat. Az első két mintát a ’sokasag1’ nevű sokaságból vettem ki, míg a harmadikat a ’sokaság2’-ből. Ezekkel az a célom, hogy bemutassam a kétmintás t-próba működését akkor, amikor a két mintát ugyanabból a sokaságból vettem ki, és akkor is, amikor a két minta egymástól különböző sokaságokból származik.

Nézzük meg a három minta átlagát és szórását:

Az eredményekből elsősorban azt lehet látni, hogy a a ’sokasag2’-ből kivett harmadik minta átlaga jelentősen nagyobb, mint az első két minta átlaga. A három minta varianciája egy kicsit más képet mutat. Az első két minta varianciája között egy kicsivel nagyobb eltérés látszik (7,324 – 5,161 = 2,163), míg a második és a harmadik minta varianciája közelebb van egymáshoz (8,696 – 7,324 = 1,372) annak ellenére, hogy ők különböző sokaságokból származnak. Mivel az F-próbát még nem ismerjük, ezért a minták varianciáit nem tudjuk egyelőre leellenőrizni, ezért a körülmények miatt úgy döntöttem, hogy az első két minta vizsgálatakor mindkét típusú t-próbát lefuttatom, míg a második és harmadik minta esetében azt feltételezem, hogy a két minta varianciája eltérő, hiszen igazolhatóan nem ugyanabból a sokaságból származnak.

Nézzük, milyen paraméterekkel hívtam meg a ’t.test()’ függvényt. Az első két paraméter értelemszerűen a ’minta1’ és a ’minta2’ adatsorok, azaz a ’sokasag1’ nevű adathalmazból kivett minták. Az ’alternative =’ paraméterrel azt tudjuk megadni, hogy egyoldali legyen-e a teszt (jobbról = „greater” vagy balról = „less”, vagy kétoldali = „two.sided”). Erről részletesebben a következő cikkben írtam (Igaz vagy hamis? – A hipotézis vizsgálatokról…). A ’var.equal =’ paraméter egy logikai változó, amely azt adja meg, hogy a két minta varianciáját egyformának tekintjük-e (TRUE) vagy sem (FALSE). Ennek függvényében fogja a függvény a kétmintás t-próbát (TRUE) vagy a Welch’s teszt (FALSE) segítségével összehasonlítani a két adatsort. A ’conf.level =’ paraméter pedig a teszt megbízhatósági szintjét adja meg (0,95, 0,99 vagy más).

A teszt eredményeként a következőt kaptam.

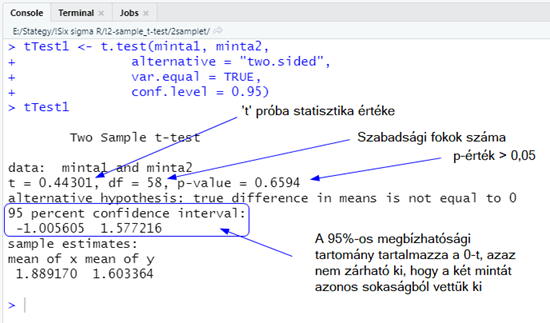
Vagyis az előzetes várakozásainknak megfelelően nincs elegendő bizonyítékunk arra, hogy a két mintát nem ugyanabból a sokaságból vettük ki.

Mivel korábban azt írtam, hogy nem ellenőriztem, hogy a két minta varianciája megegyezik-e vagy sem, ezért most nézzük meg, mit ad ki a Welch - teszt.

Mint látható, a kapott eredmények nagyon hasonlítanak az előzőhöz, ennek titka szerintem az, hogy a két minta átlaga nagyon közel van egymáshoz (1,88917 vs. 1,60336)

Most viszont nézzük meg azt, hogy néz ki, amikor a két mintát két különböző sokaságból vesszük ki.

Ez esetben a Welch’s teszt alapján egyértelműen elvetjük a nullhipotézist, azaz biztos vagyok abban, hogy a két mintát NEM VEHETTÜK KI ugyanabból a sokaságból.

Összegzés:

A cikkben igyekeztem részletesen bemutatni a kétmintás t-próbák kiválasztását, elvégzésük módját R-ben és az eredmények értelmezését. A minták varianciáinak összehasonlításával még adós maradtam, ezt majd egy későbbi cikkben fogom bemutatni.

Források:

Michael "Jack" Davis: Two-sample t-tests, Simon Fraser University, Canada
https://www.sfu.ca/~jackd/Stat203_2011/Wk07_1_Full.pdf

Wikipédia – Kétmintás t-próba
https://hu.wikipedia.org/wiki/K%C3%A9tmint%C3%A1s_t-pr%C3%B3ba

Wikipedia – Welch’s test
https://en.wikipedia.org/wiki/Welch%27s_t-test#Calculations

Berkeley Statistics - Using t-tests in R
https://statistics.berkeley.edu/computing/r-t-tests