Az egymintás t-próba esetében (Z helyett t – leheletnyi különbség) még mindig volt egy sokaságunk, noha nem ismertük a szórását. Akkor most elimináljuk a kiinduló feltételek közül a sokaság utolsó írmagját is, azaz a sokaság átlagát. Így elérjük azt az állapotot, amikor már semmit sem tudunk a sokaságról. Rendben, de akkor mihez fogjuk hasonlítani a kis mintánkat?
Természetesen nem esünk kétségbe, ha nincs sokaság, amihez hasonlítani tudnánk, akkor veszünk egy másik mintát is, és a két mintát hasonlítjuk össze. Ha jobban belegondolok, akkor az eddig ismertetett statisztikai tesztek közül leginkább ez az eset szokott előfordulni a gyakorlatban. Mármint az, hogy a vizsgálandó sokaságról semmit sem tudunk. Ezért, ha valamilyen változás hatását szeretnénk megvizsgálni, akkor veszünk egy olyan mintát, ahol a vizsgált hatás nem érvényesül, illetve egy másik mintát, ahol a vizsgált hatás érvényesül, majd összehasonlítjuk ezek átlagát, hogy megváltozott-e az eredmény.
Ez esetben Samu nem azzal dicsekszik, hogy milyen magas átlagos pontszámot tud elérni hosszútávon, ehelyett azt állítja, hogy ő öt feles után is ugyanolyan jól játszik, mint teljesen józanon. Erre azt mondod, hogy rendben, de tegyünk egy próbát és felajánlod, hogy játsszatok 3 mérkőzést józanon, majd játszatok le 5 meccset úgy, hogy Samu minden menet előtt megiszik egy fél pálinkát. Ezután összehasonlítjátok a kétféle állapotban lejátszott meccsek átlagait, hogy meglássuk, van-e hatása a feleseknek. Vegyünk észre azonban néhány apróságot:
- Nem akarunk három napig egyfolytában játszani és Samu sem akar teljesen lerészegedni, tehát relatíve kevés mérkőzés alapján kell döntést hoznunk. Nem tudunk harmincnál több mintát venni a két esetből, tehát Student-féle t-eloszlást kell alkalmaznunk.
- Nem kötelező, hogy Samu józanon és piásan is ugyanannyi mérkőzést játsszon, a két minta mintaszámának nem kell megegyeznie.
- Az sem kötelező, hogy a józanon és az italos állapotban játszott mérkőzések eredményeinek szórása megegyezzen (minden ellenkező híresztelés ellenére).
Akkor most elemezzük egy kicsit mélyebben, hogy mi is történik ebben a helyzetben. Samu először józanon lejátssza a három meccsét és a következő eredményeket kapja:
120 pont
115 pont
125 pont
Átlag (Xj) = 120 pont
Szórás (Sj) = 5 pont
Minták száma (nj) = 3
Ezután játszik öt mérkőzést úgy, hogy mindegyik előtt megiszik egy féldeci körtepálinkát. Így az eredményei a következők:
95 pont
90 pont
85 pont
60 pont
45 pont
Átlag (Xr) = 75 pont
Szórás (Sr) = 21,5 pont
Minták száma (nr) = 5
Ha egy kicsit jobban belegondolunk, akkor a józanon lejátszott három mérkőzés a józanon lejátszott mérkőzések SOKASÁGÁBÓL származik, az italos állapotban lejátszott öt mérkőzés pedig az italosan lejátszott mérkőzések SOKASÁGÁBÓL lett kivéve. A következőket tudjuk:

Nullhipotézisnek megadhatnánk azt, hogy a józanon lejátszott mérkőzések és az italosan lejátszott mérkőzések átlaga legyen egyenlő, azaz Xj = Xr. Ekkor azonban nem egy olyan t-eloszlást kapunk, amelynek az átlaga 0. Ennél van egy bölcsebb megoldás is, legyen a nullhipotézis az, hogy a két minta átlagának különbsége 0, az ellenhipotézis pedig az, hogy a két minta átlagának különbsége NEM 0! Hogyan kapjuk meg így ’t’ értékét?
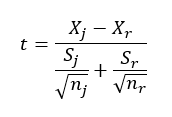
A számlálóban van a két minta átlagának különbsége, eddig ez egyszerű. A nevezőben lévő összeg két tagjának formátuma már ismerős lehet, hiszen a Centrális Határeloszlás tétele (A nagy dobókocka kísérlet) kimondja, hogy a sokaságból kivett minták átlagainak átlaga megegyezik a sokaság átlagával, szórása pedig megegyezik a sokaság szórásának és a mintaszám négyzetgyökének hányadosával. És tényleg, mivel két egymástól - elvileg - különböző sokaságból kivett n-elemű mintát vizsgálunk, így a mintaeloszlás tulajdonságait kell használnunk a hipotézisünk vizsgálatakor. Felhívom a figyelmet arra, hogy noha a számlálóban a két minta átlagát kivontam egymásból, a nevezőben a szórások összeadódnak!
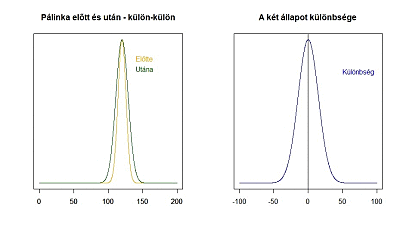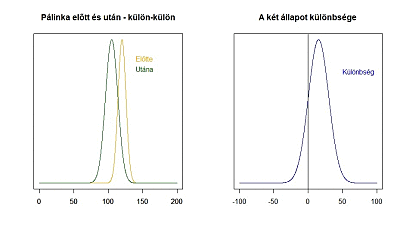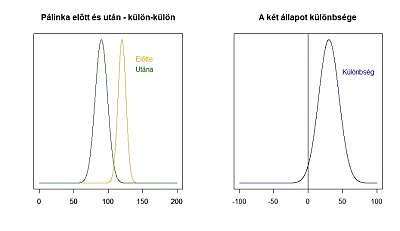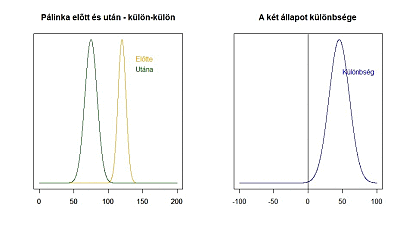 Az animáció bal oldalán látható a két mintához tartozó sokaság és ezek egymáshoz képesti helyzete, a jobb oldalán pedig a két mintaátlag különbségének sokasága, amelynek átlaga 0, ha a két sokaság átlaga megegyezik és ahogy egyre nagyobb a különbség a két minta átlaga között, a sokaság átlaga annál messzebb kerül a 0-tól. Hogy mikor jön el az a pont, amikor már biztos, hogy nem lehet a két mintaátlag különbsége 0, az függ egyrészt a két átlag szórásától, illetve a két átlag mintaszámától. Minél nagyobb a két szórás, annál nagyobb lesz az összegzett szórás és állandó szórások esetén minél nagyobbak a mintaszámok, annál kisebb lesz az összegzett szórás!
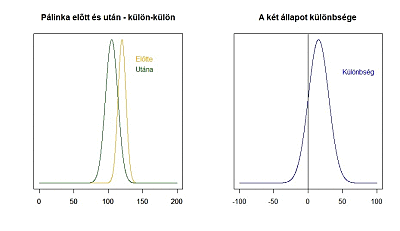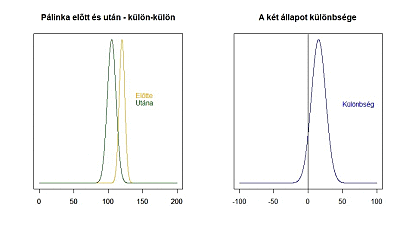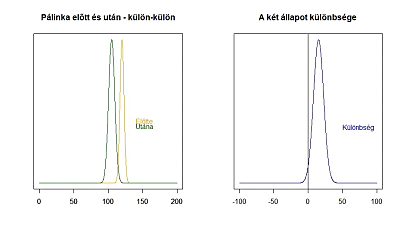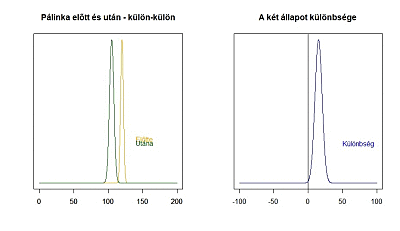
Az animáció bal oldalán látható a két mintához tartozó sokaság és ezek egymáshoz képesti helyzete, a jobb oldalán pedig a két mintaátlag különbségének sokasága, amelynek átlaga 0, ha a két sokaság átlaga megegyezik és ahogy egyre nagyobb a különbség a két minta átlaga között, a sokaság átlaga annál messzebb kerül a 0-tól. Hogy mikor jön el az a pont, amikor már biztos, hogy nem lehet a két mintaátlag különbsége 0, az függ egyrészt a két átlag szórásától, illetve a két átlag mintaszámától. Minél nagyobb a két szórás, annál nagyobb lesz az összegzett szórás és állandó szórások esetén minél nagyobbak a mintaszámok, annál kisebb lesz az összegzett szórás!
 Annak reményében, hogy ennyi elmélkedés elég ahhoz, hogy a kétmintás t-próba alapelve megértésre talál, térjünk vissza Samu alkoholtesztjéhez a feladathoz. Ha kiszámolom 't' értékét a fenti képlet alapján, a következő eredményt kapom:
Annak reményében, hogy ennyi elmélkedés elég ahhoz, hogy a kétmintás t-próba alapelve megértésre talál, térjünk vissza Samu alkoholtesztjéhez a feladathoz. Ha kiszámolom 't' értékét a fenti képlet alapján, a következő eredményt kapom:
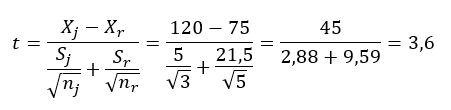
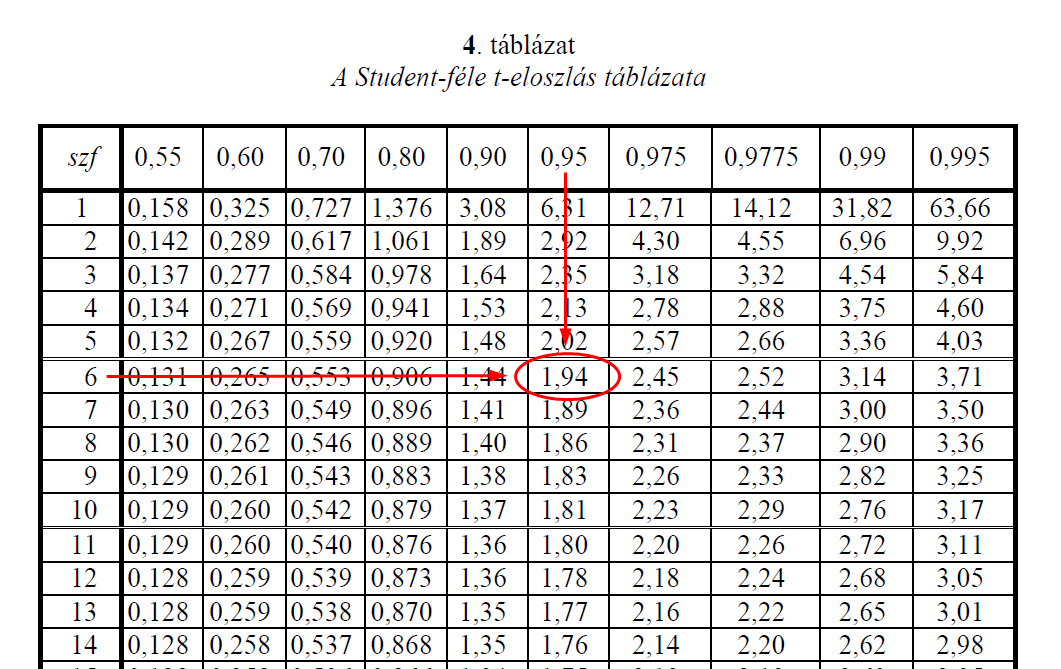
Ok, de mennyi lesz a döntési határérték t-re és hogyan számolom ki a megbízhatósági intervallumot? A döntési határérték meghatározása ugyanaz, mint az egymintás t-próba esetében, egyedül arra kell vigyázni, hogy itt a szabadsági fok (szf) nj + nr - 2 = 3 + 5 -2 = 6 lesz! Ez alapján a döntési határérték 1,94 lesz. Mivel fentebb kiszámoltuk, hogy 't' értéke 3,6 és ez jelentősen nagyobb, mint a döntési határérték, a nullhipotézist elutasítom és kijelentem, hogy a két minta átlaga NEM EGYEZHET meg, azaz Samu eredményére igenis hatással voltak az elfogyasztott röviditalok.
A megbízhatósági intervallum kiszámítása hasonlóképpen zajlik, mint az előzőekben, azaz 't' helyére be kell helyettesíteni a megfelelő döntési határértéket és ki kell fejezni az intervallum alsó és felső határát.
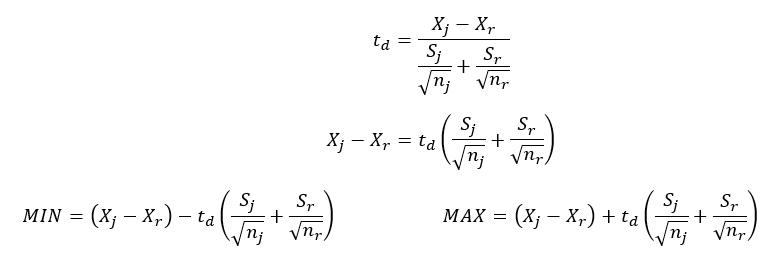
A megfelelő értékeket a képletekbe behelyettesítve megkapjuk a két mintaátlag különbségének megbízhatósági intervallumát:
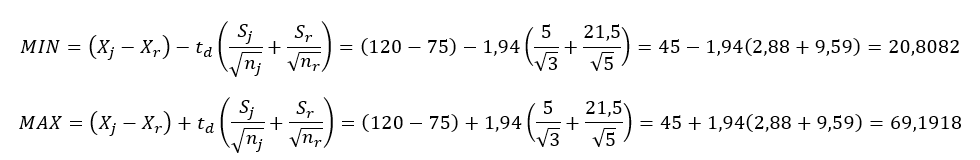
Tehát a két mintaátlag különbsége a 20,8082 - 69,1918 tartományba esik bele. Mivel ebben a tartományban a 0 nincs benne, ezért a nullhipotézist ELUTASÍTOM.
Utolsó megjegyzésként kiemelem, hogy ezt a képletet sem így tanuljuk az iskolában, 't' értékének kiszámítása a tankönyvekben a következő módon szerepel:
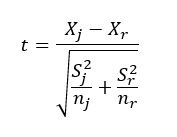
A képletet egy kicsit tüzetesebben megvizsgálva feltűnik, hogy a tört számlálója ugyanaz, a nevező változott csak meg. Először is Sj és Sr négyzetre emelve bekerült a gyökjel alá, majd a két tört szintén összevonásra került a gyökjel alatt. Ismét egy briliáns példa arra, hogy egy képlet átalakításával hogyan lehet elrejteni az egész módszer lényegét az avatatlan szemlélő elől.





