Az előző bejegyzésben (Z, mint Z-próba…egymintás!) tisztáztuk, hogy mit jelent az egymintás Z-próba. Mivel ismertük a sokaság átlagát és szórását is, ezért lehetett a normál eloszlást használni. Akkor most lépjünk egyet előre és nehezítsük meg a dolgunkat egy kicsit. Mi történik akkor, ha Samu csak annyit tud nekünk mondani, hogy ő hosszútávon 150 pontos átlaggal teljesítette a mérkőzéseit, de nem tudja megmondani, hogy milyen szórással, azaz nem tudja megadni a sokaság szórását?

Ez gond, hiszen a  

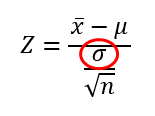képlethez hiányzik a szórás értéke! Persze mondhatjuk azt, hogy semmi gond, éppen van nekünk egy szórásunk kéznél, csak az nem a sokaság szórása, hanem a mintánk szórása. Mi lenne, ha azt helyettesítenénk be a képletbe és nem a sokaság szórását? Elsőre ez egy egészen jó ötletnek tűnik, de aztán kénytelenek vagyunk egy kicsit elgondolkodni. A Centrális Határeloszlás tétele ugyan kimondja, hogy a sokaságból kivett minták átlagainak eloszlása normál eloszlást követ és szórása megegyezik a sokaság szórásának és a mintaszámnak a hányadosával, de ez csak akkor igaz, ha a sokaságunk mérete meghalad egy bizonyos mértéket! Addig, amíg a sokaságunk akár több tucat vagy akár több száz mérkőzés eredményének a halmaza, addig a mintánkban összesen három (!) mérkőzés eredményéből számoljuk ki a szórást!

De ha egy kis elemszámú minta szórását használom fel a sokaság szórása helyett, akkor az ezekből képzett minták eloszlása már nem lesz normál eloszlású! Ha nem lesz normál eloszlású, akkor viszont nem igazak rá a normál eloszlásra jellemző törvényszerűségek sem, tehát nem vezethetem vissza a képlet eredményét a standard normál eloszlásra.

Itt jön be William S. Gosset, ami kedves sörfőző barátunk. A róla szóló cikkben (A sörfőző, aki forradalmasította a statisztikát) tisztáztuk, hogy Gosset úr pontosan ezt kutatta. Azt, hogy milyen eloszlása van a kis elemszámú mintáknak. Ebben az előző cikkben azt is tisztáztuk, hogy a tehetséges matematikus pontosan arra jött rá, hogy ezek a kis elemszámú minták egy a normál eloszláshoz hasonló mintázatot követnek, az úgynevezett Student-féle t-eloszlást. Az alábbi grafikonon jól látható, hogy kis elemszámok esetében a Student-féle t-eloszlás által megadott valószínűségek jelentősen eltérnek a standard normál eloszlás által megadott valószínűségektől!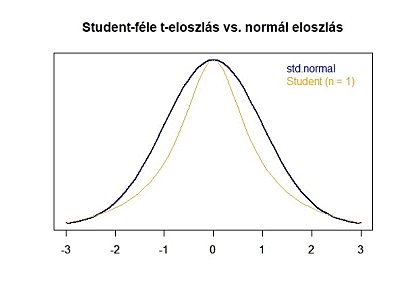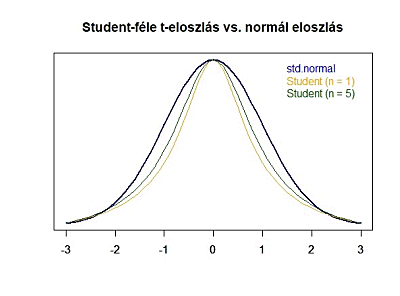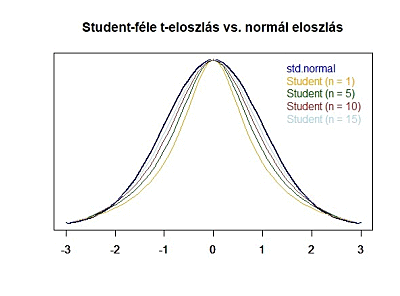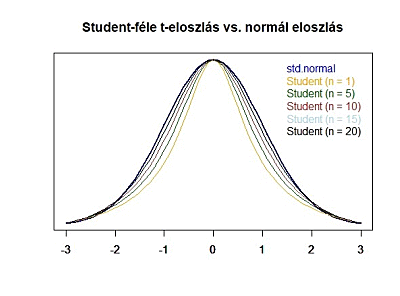Tehát akkor mégiscsak van megoldás! Ugyanazt fogjuk tenni, mint az egymintás Z-próba esetében, csak a sokaság szórása helyett – amit nem ismerek – a Samu által lejátszott három mérkőzés eredményeinek szórását fogom behelyettesíteni a képletbe. A másik különbség csakis annyi lesz, hogy a végén a képlet eredményét nem a standard normál eloszlás függvénybe, hanem a Student-féle t-eloszlás képletébe helyettesítem be, és így kapom meg keresett valószínűséget. Ez alapján a képlet eredményét nem is ’Z’-vel, hanem ’t’-vel fogom jelölni, hiszen a Z betűt fenntartom a standard normál eloszlás számára. Vagyis az egymintás t-próbához használt képlet a következő:

ahol az ’s’ betű a Samu által az orrom előtt lejátszott három mérkőzés szórása lesz. Így tehát ’t’ értékének kiszámítása semmivel sem bonyolultabb, mint az egymintás Z-próba esetében. Csakhogy van még egy aprócska probléma, mégpedig az, hogy ha Samu három, négy, vagy öt meccset játszik le, a mintaszámtól függően mindig másik t-eloszlást kell alkalmazni, csak így lesz pontos az eredmény. Amíg az egymintás Z-próba esetében csak egyetlen standard normál eloszlás létezik, tehát 95%-os, a 99%-os és a 99,9%-os döntési kritériumokat csak egyszer kell meghatározni és utána csak használni kell őket, itt sajnos minden egyes esetben a figyelembe vett mérkőzések számának függvényében minden egyes vizsgálathoz külön-külön ki kell számolni.

Vagyis nézzük meg, hogy milyen eredményt kapunk, ha egymintás t-próbával számoljuk végig az előzőekben ismertetett feladatot. Milyen adatokat is használtunk fel az előző bejegyzésben?

Samu azt állította, hogy hosszútávon képes 150 pontos átlagot tartani, tehát a sokaság átlaga (mü) egyenlő 150-nel. Samu a velünk játszott három mérkőzés során 120 pontos átlagot hozott, tehát a mintánk átlaga 120 pont. A minta szórását az előző példában nem adtam meg, hiszen azt nem használtuk fel a Z-próba kiszámításakor. Tegyük fel, hogy a három mérkőzés során Samu a következő eredményeket hozta:

1.       mérkőzés: 100 pont

2.       mérkőzés: 145 pont

3.       mérkőzés: 115 pont

A három mérkőzés átlaga 120 pont

A három mérkőzés szórása 22,91 ≈ 23 pont

Mivel megvan minden szükséges adatunk ’t’ kiszámításához, akkor tegyük azt meg:

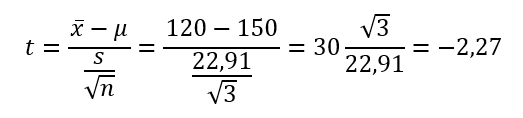
Ha a négyjegyű függvénytáblázatban megnézed a Student-féle t-eloszlás táblázatát, azt fogod látni, hogy a felépítése jelentősen különbözik a standard normál eloszlás táblázattól. A t-eloszlás táblázatban az egyes sorok az úgynevezett szabadsági fokokat tartalmazzák, amit úgy határozunk meg, hogy a mintaszámból kivonunk egyet, azaz jelen esetben – mivel Samu három mérkőzést játszott le – a szabadsági fokok száma 2 lesz. Ha elegendő 95%-os megbízhatósági szinten döntést hoznunk és az egymintás Z-próbához hasonlóan itt is egyoldali tesztet végzünk, mert arra számítunk, hogy Samu kevesebb pontot ér el, mint 150, akkor az alábbi táblázatból az szf=2 sor és a 0,95 oszlop kereszteződésében található számot kell kiválasztanunk, ami ez esetben 2,92, illetve -2,92, hiszen a Student-eloszlás ugyanúgy szimmetrikus, mint a normál eloszlás.

Tehát az egymintás t-próba jelen esetben azt mutatja, hogy ha Samu a három mérkőzés alatt a fenti eredményeket hozta, akkor egyértelműen nem zárható ki, hogy hasonló teljesítménnyel képes hosszútávon átlagosan 150 pontos teljesítményre. Persze vegyük figyelembe, hogy amíg az előző példában a sokaság szórása 8,33 pont volt, itt a minta szórása 23 pont, ami lényegesen nagyobb. Nyilvánvaló, hogy minél több mérkőzést játszi Samu, azaz minél több minta alapján hozzuk meg a döntésünket, annál biztosabb lesz a döntés, hiszen jól látható, hogy minél nagyobb a szabadsági fokok száma, annál kisebb lesz a 95%-os megbízhatósági szint értéke.

Természetesen ez esetben is fel tudjuk tenni a kérdést, hogy mennyire kellene Samunak „rosszul” játszania a három mérkőzés alatt, hogy már ne tudjuk elhinni ez alapján, hogy Samu képes a 150 pontos átlagra. Az eljárás itt is hasonló, mint az egymintás Z-próba esetében, vissza kell helyettesíteni a t-eloszlás táblázatból kinyert -2,92-t az ismert képletbe és ki kell fejezni a mintaátlagot:

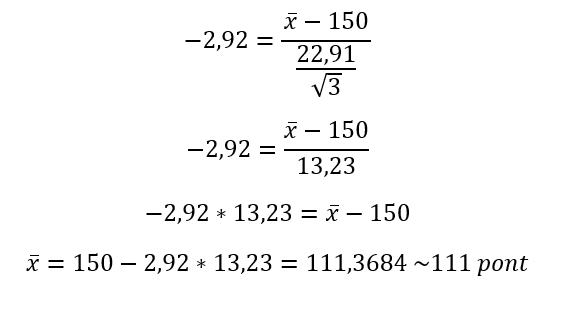azaz, ha Samu a három meccsen 111 pontnál kevesebbet ért volna el, akkor nem hinnénk el neki, hogy képes hosszútávon 150 pontos átlagot teljesíteni.

Végül - rossz szokásomhoz híven - ismét készítettem egy kis táblázatot, most elkezdtem összehasonlítani a standard normál eloszlás és a Student-féle t-eloszlás értékeit -3 és +3 közötti x-értékekre, majd vettem ezek különbségét fokozatosan növelve a mintaszámot. Az alábbi grafikonon a kétféle eloszlás különbsége látható a mintaszám függvényében.

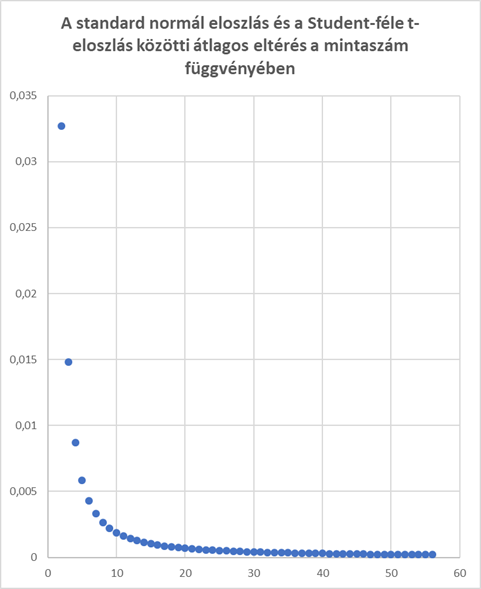
Jól érzékelhető, hogy 30-40 feletti mintaszámoknál a kétféle eloszlás különbsége már elenyészően kicsi, szóval ennél nagyobb elemszámú minták esetében az egymintás Z-próba és az egymintás t-próba eredménye közötti eltérés elhanyagolható, azaz ilyen esetekben mindkét teszt egyformán alkalmazható. De ezt már próbáljátok ki magatok!

A következő bejegyzésben megmutatom majd, hogy hogyan lehet az egymintás t-próbát kiszámítani táblázatkezelő program segítségével.