Korábban már részletesen tárgyaltam a hipotézis vizsgálatok lényegét és menetét (Igaz vagy hamis – a hipotézis vizsgálatokról…). Most pedig vágjunk bele az első hipotézis vizsgálatba, amelynek már konkrét haszna is van. A próba neve egymintás Z-próba, ami a mezei olvasónak természetesen igencsak semmitmondó. A Z-betű természetesen nem Zorróra utal, bár tartok tőle, hogy mire a végére érünk, úgy fogod érezni magad, mintha Zorró vágott volna egy X-et a homlokodra.

A viccet félretéve, ha még emlékszel a standardizálásról szóló bejegyzésre (Első az egyenlők között – a standard normál eloszlás), az ott kiszámolt 'x’ értékét a legszebb statisztikusi hagyományok jegyében Z-betűvel szokták jelölni. Azért egymintás, mert ebben az esetben egy több elemből álló minta tulajdonságait hasonlítjuk egy sokaság tulajdonságaihoz, ahogy azt majd a későbbiekben részletesebben kifejtem majd.

De mire is jó ez a teszt?

Az egyszerűség kedvéért maradjunk a korábban hivatkozott bejegyzésben már elkezdett bowling példánál. Samu azt állítja, hogy az elmúlt öt év alatt lejátszott mérkőzéseinek átlaga 150 pont és a mérkőzéseinek eredményei valahol 105 és 195 pont között voltak. Ez alapján feltételezhetjük, hogy a mérkőzések eredményeinek szórása 15 pont, ha feltételezzük, hogy az eredmények legnagyobb része a plusz-mínusz háromszoros szórás által kijelölt tartományban van (150 pont ± 3 x 15 pont).

A fent már meghivatkozott előző posztban azt mondtuk, hogy érzésre azt mondjuk, hogy ha Samu 120 pontnál többet teljesít, akkor elfogadjuk az állítását, ha pedig ennél kevesebbet, akkor elutasítjuk. De a 120 pontos határ, az igazából egyfajta megérzés alapján került meghatározásra, nem pedig ismert tények alapján. Ha Samu korábbi eredményei alapján 150 pontos átlaggal és 15 pontos szórással teljesített, akkor a 120 pontos határ jó, vagy sem? Tévedünk-e, ha Samu 119 pontos átlagot hoz az előző posztban említett 3 mérkőzés alatt és mi azt mondjuk neki, hogy hazudott?

Az Egymintás Z-próba abban segít nekünk, hogy előre megadott biztonsággal meg tudjuk mondani, hogy a Samu által a jelenlétünkben lejátszott 3 mérkőzés – a minta - átlaga alapján igaz lehet-e Samu állítása.

A teszt végrehajtása

Először is határozzuk meg a nullhipotézis (H0) és az ellenhipotézist (H1). A nullhipotézis esetünkben az, hogy a 3 mérkőzés alapján elhisszük, hogy Samu hosszútávú átlaga 150 pont. Az ellenhipotézis ennek az ellenkezője, azaz nem hisszük el neki, hogy képes hosszútávon 150 pontos átlagot tartani.

Aztán vannak a tesztnek bizonyos előfeltételei, de ezzel most nem fárasztanálak. Majd, ha eljön az ideje, akkor megtanulod.

Tehát van egy sokaságunk, aminek ismerjük az átlagát és a szórását, illetve van egy mintánk, a 3 mérkőzés, amit Samu az orrunk előtt játszott le. A nagy dobókocka kísérlet című bejegyzésben elemeztem, hogy ha van egy sokaságunk és abból kiveszünk egy jelentős mennyiségű mintát, majd megvizsgáljuk ezen minták átlagainak eloszlását, akkor azt fogjuk kapni, hogy

• a mintaátlagok normál eloszlású mintázatot mutatnak,
• a mintaátlagok átlaga megegyezik a sokaság átlagával,
• a mintaátlagok szórása pedig megegyezik sokaság szórásának és a mintaszám négyzetgyökének hányadosával.

Ezt nevezzük a Centrális Határeloszlás tételének. Jelen esetben ezt a tételt fogjuk kihasználni.

Ha Samuval nemcsak egyszer 3 mérkőzést játszattunk volna le, hanem mondjuk ezerszer 3 meccset, majd ezeknek a 3 mérkőzéses sorozatoknak vennénk az átlagait, majd megvizsgálnánk a mintaátlagok eloszlását, akkor a Centrális Határeloszlás tétele alapján azt kapnánk, hogy az ezer darab mintaátlag átlaga megegyezik a sokaságunk átlagával, azaz 150-nel, a mintaátlagok szórása pedig megegyezik a sokaság szórásának és a mintaszám négyzetgyökének a hányadosával, azaz 15 osztva gyök alatt 3-mal, tehát 15 / 1,73 = 8,66-tal.

Kérdés, hogy a Samu által most lejátszott 3 mérkőzés eredményének átlaga esetében lehetséges-e, hogy 

És itt jön be a standardizálás (Első az egyenlők között – a standard normál eloszlás), tehát az, hogy a mintaátlagok eloszlását visszavezetjük a standard normális eloszlásra, amelynek az átlaga 0 és a szórása 1. Mit tudunk jelenleg?

A sokaság átlaga (mu) 150 pont

A sokaság szórása (X-átlag) 15 pont

A Samu által lejátszott 3 mérkőzés átlaga 120 pont.

Ha mindezeket átszámoljuk a standard normál eloszlásra, akkor a következőket kapjuk:

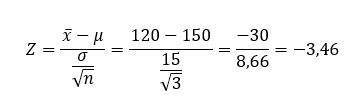
Ez vizuálisan valahogy így néz ki:

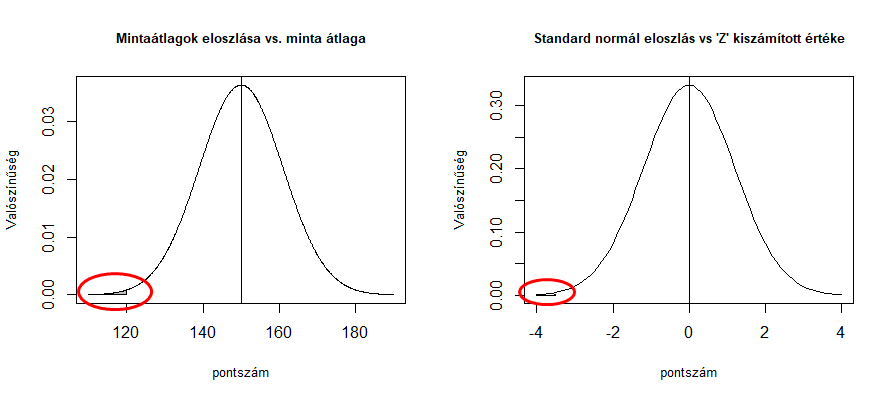
Akkor most ezt a Z értéket össze kell hasonlítanunk azzal a határértékkel, amit az előző cikkben szereplő módon a egyoldali vagy kétoldali ellenhipotézis és a megbízhatósági szint alapján választunk ki.

Jelen esetben erősen gyanítom, hogy Samu teljesítménye rosszabb lesz, mint a sokaság, ezért baloldali ellenhipotézissel számolok. A hipotézis vizsgálatokról szóló cikkben említettem, hogy többféle megbízhatósági szintet (konfidencia szint) meg lehet határoznia annak függvényében, hogy mennyire fontos az, hogy ne hibázzunk. Ez a megbízhatósági szint lehet 95%, 99% vagy akár 99,9% is.

A standard normál eloszlás esetén – mivel ebből csak egy van – egyszerűen előre meg vannak határozva azok a szintek, amelyeket figyelembe kell venni:

Ezeket az értékeket a normál eloszlás függvény segítségével (Első az egyenlők között - a standard normál eloszlás) számították ki, ezek mindig állandóak, hiszen standard normál eloszlásból csak egy van.

Úgy gondolom, hogy a döntést elegendő 95%-os valószínűséggel meghoznom, mert Samu csak a haverom és nem aggódom egy esetleges téves következtetés következményei miatt. Jelen esetben baloldali ellenhipotézissel számolok, mert arra számítok, hogy a Samu által lejátszott 3 menet átlaga KISEBB lesz, mint az általa bizonygatott 150 pont. Így az általam választott döntési határérték -1,64 lesz.

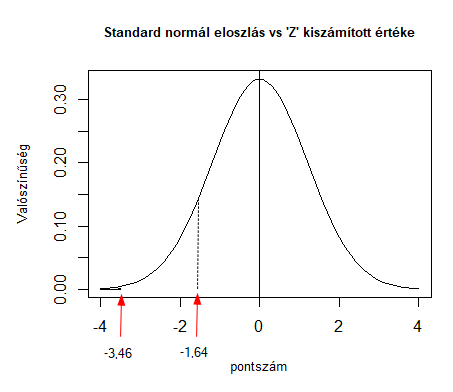
• Mivel ez NAGYOBB, mint a megállapított határérték, ezért a nullhipotézist (H0) elvetem, és elfogadom az ellenhipotézist (H1), azaz szerintem Samu nem állított igazat, amikor azt mondta, hogy az ő hosszútávú átlaga 150 pont, vagy egyszerűen csak elfogadom, hogy eggyel több sört ivott a kelleténél.
• Ha biztosabb akarok lenni, akkor választhatok 99%-os valószínűséget is, ekkor -2,32 lesz a döntési határérték, de a kapott Z értéke még ennél is kisebb, tehát még ekkor is elvetem a nullhipotézist.
• 99,9%-os valószínűség esetén a határérték -2,54 lesz. Mivel ez is sokkal kisebb, mint az általunk kapott Z-érték, ezért a nullhipotézist ezen megbízhatósági szinten is elvetem.

Utolsó kérdésként felmerülhet, hogy mekkora kell, hogy legyen a sokaság átlaga ahhoz, hogy a minta alapján elfogadjam a nullhipotézist. Ehhez Z helyére be kell helyettesíteni az előbb alkalmazott -1,64-es határértéket, majd az egyenletből ki kell fejezni a sokaság átlagát:

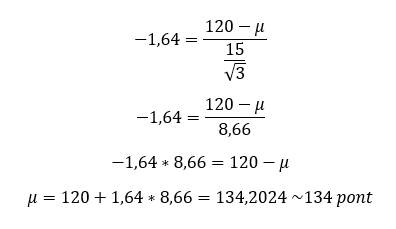
Mivel egyoldalas hipotézis vizsgálatot végeztünk, ezért csak ezt a legkisebb mu értéket számoltuk ki, amelyet még elhiszünk a 3 mérkőzés eredménye alapján. A statisztikai programok általában ezt számolják ki konfidencia intervallumként.

Ez alapján Samunak azt még elhiszem a 3 mérkőzés eredményei alapján, ha azt mondja, hogy hosszú idő és rengeteg mérkőzés átlagában 134 pontos átlagot képes hozni, de ennél magasabbat már nem!

Ettől függetlenül azt a kérdést is feltehetjük, hogy legalább mekkora kellene, hogy legyen a 3 menet eredménye ahhoz, hogy elfogadjam a nullhipotézist? Az eljárás igazából ugyanaz, tehát behelyettesítem az elfogadási kritériumot Z helyére és átrendezem az egyenletet úgy, hogy megkapjam a kívánt mintaátlagot:

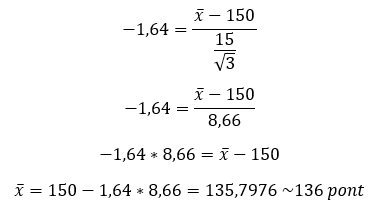
Azaz Samunak legalább 136 pontos átlagot kellene hoznia ahhoz, hogy elhiggyem, hogy képes a 150 pontos átlagra 15 pontos szórással. Hangsúlyozom, hogy noha Samu az elején azt állította, hogy a korábbi mérkőzéseinek az eredménye 105 és 195 pont között volt, itt most 3 mérkőzés átlagára tettünk becslést. Egy-egy mérkőzés a háromból lehet kisebb, mint 136 pont, de nagyobb, mint 105 pont. Viszont kell, hogy legyenek olyan mérkőzések is, amelyeknek az eredménye annyival nagyobb, mint 136 pont, hogy a végén kijöjjön a minimum 136 pontos átlag!

Végezetül még annyit tennék hozzá a fentiekhez, hogy ha Samu képességeit nem 3 hanem 6 vagy 10 vagy akár 15 mérkőzés átlaga alapján szeretnénk megítélni, akkor kiderül, hogy minél több meccs eredményét vesszük figyelembe, annál magasabb lesz az a pontszám, amit el kell érnie, hiszen annál kisebb lesz a mintaátlagok szórása. Emlékeztetőül a korábban már közzétett grafikon:

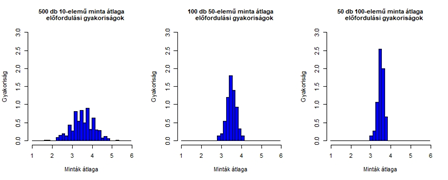
A következő cikkben ugyanennek a feladatnak egy táblázatkezelőben elkészített megoldását fogom bemutatni.