Amikor fejlesztünk valamit, akkor vagyunk elégedettek, ha látjuk a változást. Vannak olyan változások, amelyek szabad szemmel is jól láthatók, más esetekben talán nem teljesen egyértelmű a változás, ezért szükségünk lehet valamilyen bizonyítékra annak eldöntése érdekében, hogy eldöntsük, vajon van-e hatása annak, amit csináltunk. Manapság erre a kétmintás t-próbát szoktuk alkalmazni. Ez sem túl bonyolult manapság a számítógépek és a szoftverek világában, de azért sokan vannak olyanok, akiknek még ez is sok, ha statisztikáról van szó.

Milyen szerencse, hogy okos mérnökök gondolnak azokra is, akik nem annyira elvetemültek, hogy szeressenek számolni. Legalábbis a bonyolult és nehezen érthető számításokat nem szeretik. De nekik jó hírem van.

Létezik két nagyon egyszerű módszer arra, hogy ezt az előtte – utána összehasonlítást elvégezzük anélkül, hogy doktorálnunk kellene matekból. Az egyszerűbb módszerrel csak 6 (jól látod, hat!) mérésből meg lehet állapítani, hogy a tevékenységünk előtti és utáni állapota között van-e valamilyen eltérés, mégpedig úgy, hogy ez nem csak amolyan légből kapott számolgatás, hanem konkrét valószínűségszámítási és statisztikai alapja van.

Na most, hogyan néz ki egy hatásos változás?

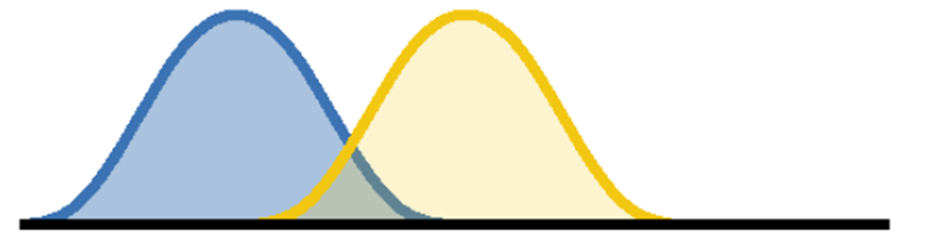
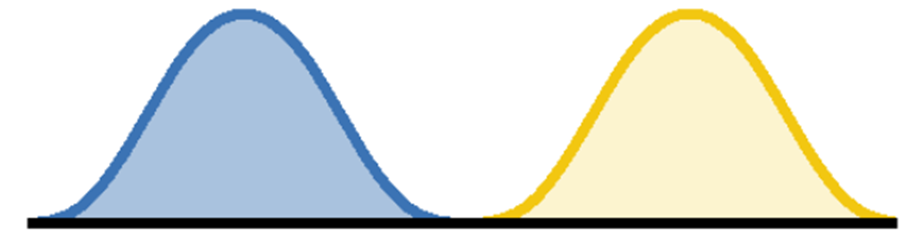
És egy nem hatásos változás?

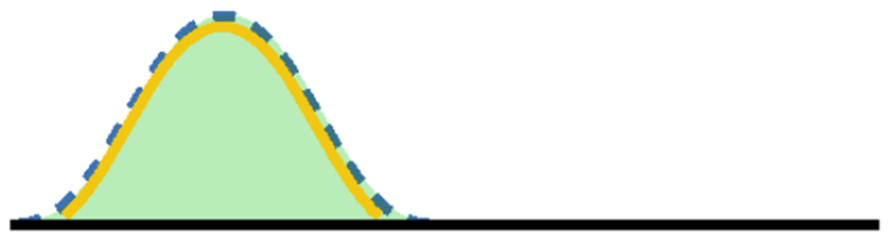
Azaz, amikor hatásos egy változtatás, akkor a ’B’ és a ’C’ folyamat görbéi teljesen elkülönülnek egymástól, illetve csak kismértékben fedik egymást. Amikor a változtatásnak nincs hatása, akkor viszont a két folyamat görbéje nagyrészt vagy teljesen fedésben vannak.

Tegyük fel, hogy van két folyamatunk, egy ’B’ folyamat és egy ’C’ folyamat. Azt várjuk, hogy a ’C’ folyamat lényegesen kisebb kimeneti értékeket fog produkálni, mint a ’B’ folyamat. Ebben az esetben a teendőnk csupán annyi, hogy kiveszünk 3 darab mintát a ’B’ folyamatból és másik három darab mintát a ’C’ folyamatból. Ha a 6 mintát nagyság szerint növekvő sorrendbe rendezzük és azt kapjuk, hogy a ’C’ folyamatból származó mindhárom eredmény kisebb, mint a ’B’ folyamatból származó eredmények, akkor kijelenthetjük, hogy a ’C’ folyamat 95%-os valószínűséggel kisebb, mint a ’B’ folyamat. Bármilyen más eredményt kapunk, akkor azt kell mondanunk, hogy nincs elegendő bizonyíték arra, hogy a ’C’ folyamat eredménye egyértelműen kisebb, mint a ’B’ folyamaté.

Ennyire egyszerű lenne? De mi ennek az alapja? Miért igaz a fenti állítás?

Igazából a magyarázat sem sokkal bonyolultabb. A történet magyarázata valahol inkább valószínűségszámítás, mint statisztika. Mi történne akkor, ha a ’B’ és a ’C’ folyamatból csak egy – egy mintát vennénk? Akkor igazából csak két különböző esetünk lenne, vagy a ’B’-ből, vagy pedig a ’C’-ből kivett minta lesz a nagyobb. Ekkor 1/2 az esélye annak, hogy az egyik vagy a másik eset fog megvalósulni (kivéve, ha egyenlőek lesznek, de most azt feltételezzük, hogy a két minta nem lehet egyenlő).

Ha a minták számát eggyel növeljük és egy mintát veszünk ki a ’B’ folyamatból és kettőt a ’C’-ből, akkor három különféle eredmény jöhet ki. Itt már 1/3 az esélye annak, hogy valamelyik kombináció kijön.

Amikor mindkét folyamatból 2 – 2 mintát veszünk ki, akkor a lehetséges kimenetek száma hatra nő, azaz a lehetséges esetek bekövetkezési valószínűsége 1/6, mint a dobókockánál.

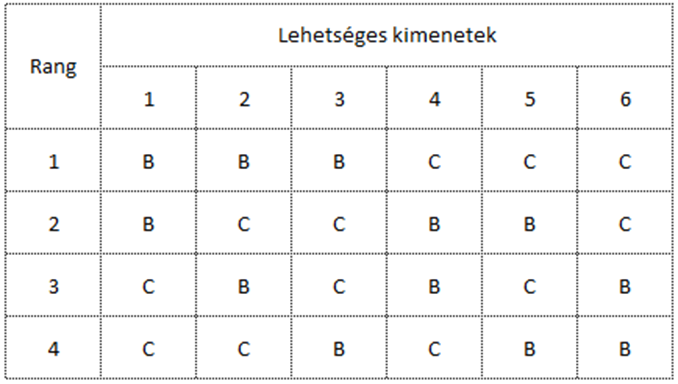
Ha még eggyel növeljük a tétet, és a ’B’ folyamatból 2, a ’C’ folyamatból 3 mintát veszünk ki, akkor már 10 különféle eredményt kaphatunk, így a lehetséges kimenetek valószínűsége 1/10 lesz.

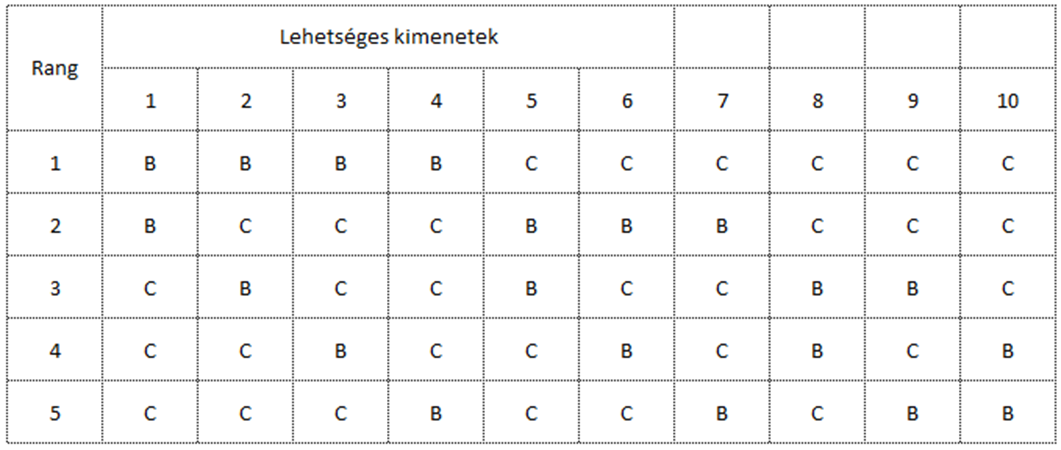
És elérkeztünk az általunk keresett esethez, amikor mindkét folyamatból 3 – 3 mintát veszünk ki, ekkor a mintáknak húszféle kombinációja lehetséges, azaz egy – egy lehetséges kimenet valószínűsége 1/20, azaz 0,05 lesz.

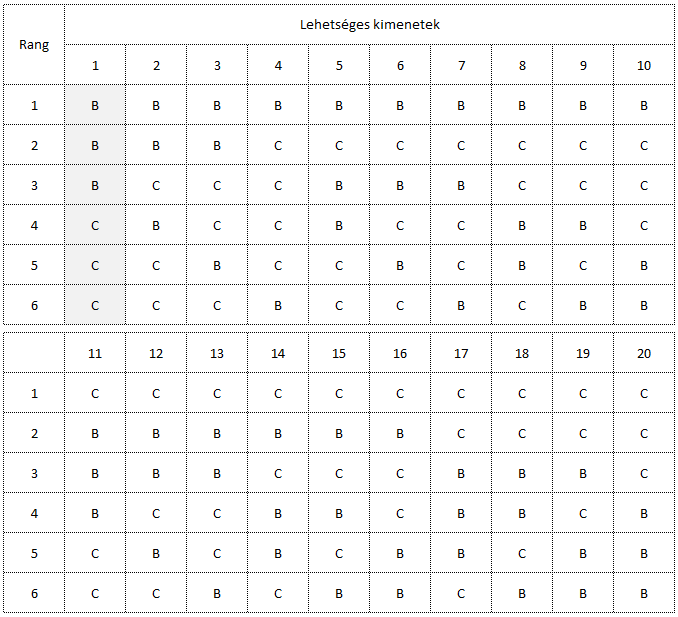
Vagyis a képen látható húszféle kombinációból pont az első eset (azaz a CCCBBB), annak pontosan 5% a valószínűsége.

Vagyis számunkra csak az az eset elfogadható, amikor a ’C’ folyamatból kivett mindhárom minta kisebb, mint a ’B’ folyamatból kivett minták. Minden egyéb esetben feltételezhetjük, hogy a két mintacsoportot olyan sokaságokból vettük ki, amelyek nem igazán különböznek egymástól. Amennyiben elfogadjuk, hogy 95%-os biztonsággal akarunk biztosak lenni abban, hogy helyesen döntünk arról, hogy a két minta érdemlegesen eltér egymástól, akkor ez csakis abban az esetben valósul meg, ha 3 - 3 mintát veszünk ki a két folyamatból és a CCCBBB sorrend alakul ki az eredmények alapján. Minden egyéb esetben azt kell feltételeznünk, hogy a ’C’ sokaság nem kisebb, mint a ’B’ sokaság!

Nos, ez egy eléggé fapados eljárás, noha ismerjük el, hogy ésszerű és a valószínűségszámítás elveinek megfelelő a megközelítés. Azonban ez nem mindig elegendő.

Amikor ez a helyzet, akkor ugyan valamivel több mintát kell kivennünk a két folyamatból (de nem sokkal többet), de egy nem sokkal bonyolultabb, viszont éppen annyival pontosabb módszert is alkalmazhatunk. Ezt a tesztet Tukey – Duckworth tesztnek hívják, természetesen a módszer két kitalálója után.

Ekkor összesen 12 – 16 darab mintát kell kivenni úgy, hogy a változtatás előtti és a változtatás utáni folyamatból egyforma mennyiségű mintát vegyünk ki, azaz kivehetünk 6 – 6, 7 – 7 vagy 8 – 8 darabot mindkét folyamatból. Ezután a mintákat ismét nagyság szerint növekvő sorrendbe rendezzük, ahogy azt az előző vizsgálatnál is tettük. Valami ilyesmi eredményt kaphatunk.

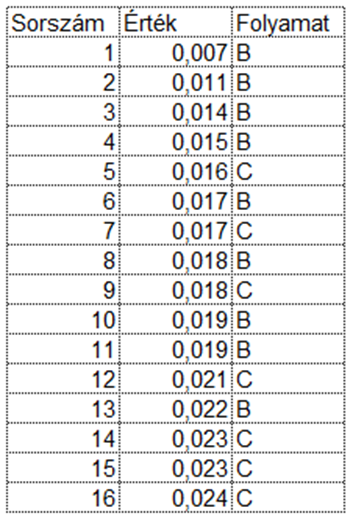
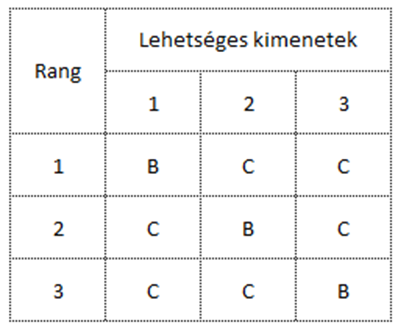
Ezután megszámoljuk, hogy a sorozat tetején hány darab ’B’ és a sorozat alján hány darab ’C’ található. Jelen esetben felül 4 darab ’B’-t és alul 3 darab ’C’-t számoltam össze, ez összesen 7 darab úgynevezett ’end-count’-ot jelent (fogalmam sincs, hogy ezt hogyan hívjam ékes magyar nyelvünkön). Tulajdonképpen ezek az ’end-count’-ok jelenítik meg a ’B’ és a ’C’ folyamatokból kivett minták eloszlásainak a két külső végét. Innentől megint csak egyszerű a dolog, mert az ’end-count’-ok száma alapján alábbi táblázatból kikereshető, hogy a két adatsor milyen megbízhatósági szinten különbözik egymástól.

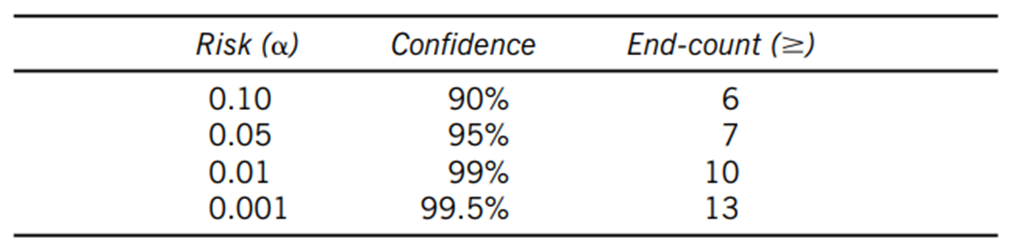
Az ’end-count’-ok összeszámolásakor egyetlen apró szabály létezik még, amire figyelni kell: Amennyiben a sorba rendezett számsor valamelyik végén van két olyan minta, amelyeknek az értéke megegyezik, de az egyik a ’B’ a másik pedig a ’C’ folyamatból származik, akkor ezt a párost csak 0,5-szörös súllyal kell beleszámolni az ’end-count’-okba.

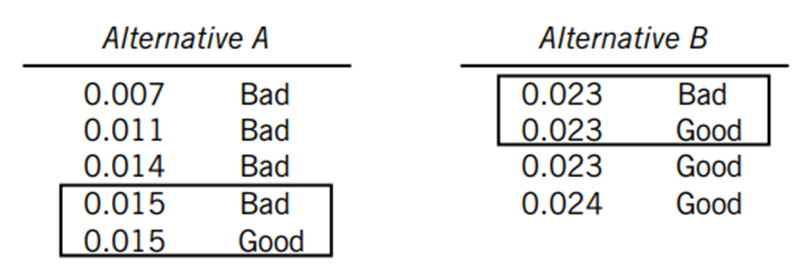
A módszer külön érdekessége, hogy az eredmény bizonyíthatóan független attól, hogy konkrétan hány mintát vizsgálunk, a 12 – 16 minta tulajdonképpen egy minimális mennyiség, amelynél kevesebbet azért nem érdemes vizsgálni, de ha több mintát veszünk ki a két folyamatból, az sem fogja befolyásolni az eredményt.

Összegzés:

A cikkben két nagyon egyszerű módszert ismertünk meg, amelyeket két adatsor összehasonlítására tudunk használni. Mindkettő igen egyszerű, gyorsan és egyszerűen elvégezhető, valamint az sem elhanyagolható szempont, hogy nem kell hozzá matekzseninek lenni. Az, hogy melyik módszert érdemes alkalmazni, az a sejtésünk dönti el, hogy mekkora a különbség a két adatsor között.

Források:

Keki Bhote: World Class Quality: Using Design of Experiment to Make It Happen, AMACOM; First Edition (November 26, 1991)

Keki R. Bhote. Adi K Bhote: World Class Quality: Using Design of Experiment to Make It Happen, Second edition Edition, AMACOM, 2000

Shainin B vs C Webinar presentation (14 – 59. oldal), ASQ
https://static1.squarespace.com/static/515082bbe4b0910b244269db/t/516d6caae4b0cdd66489b0b7/1366125738360/ASQ+Auto+Shainin+B+vs+C+Webinar.pdf