
A múlt heti cikkben (Gyártsunk mintából mintát) bemutattam azt a két elterjedt módszert a sokaság megbízhatósági tartományának meghatározására, amelyeket akkor tudunk alkalmazni, ha a hagyományos statisztikai tesztek valamilyen ok miatt nem alkalmazhatók. A cikk végén tettem egy olyan felelőtlen ígéretet, hogy kipróbálom a bootstrap módszert a gyakorlatban is.
Persze itt nem arra gondoltam, hogy széleskörű vizsgálatsorozatba kezdek, éppen csak annyit, hogy egyetlen példával összehasonlítom egy elméleti sokaság, illetve egy abból kivett minta alapján becsült megbízhatósági tartományokat és ez alapján próbálok képet alkotni arról, hogy mennyire lehet korrekt a bootstrap becslés. A vizsgálatom célja az, hogy egyetlen vizsgálat segítségével összehasonlítsam, vajon a sokaságból kivett minta alapján végzett bootstrap becslés mennyire felel meg - az ez esetben ismert - sokaságból kivett valós mintáknak, vagyis ez inkább csak egy benyomás lesz, nem egy tudományos alapú vizsgálat.
Először is létrehoztam egy 1000 elemből álló "krumpli eloszlású" sokaságot. Azért lett krumpli, hogy ha egy ilyen sokaságon működik a bootstrap, akkor van esélye annak, hogy mindenféle más eloszlásokkal is működni fog.
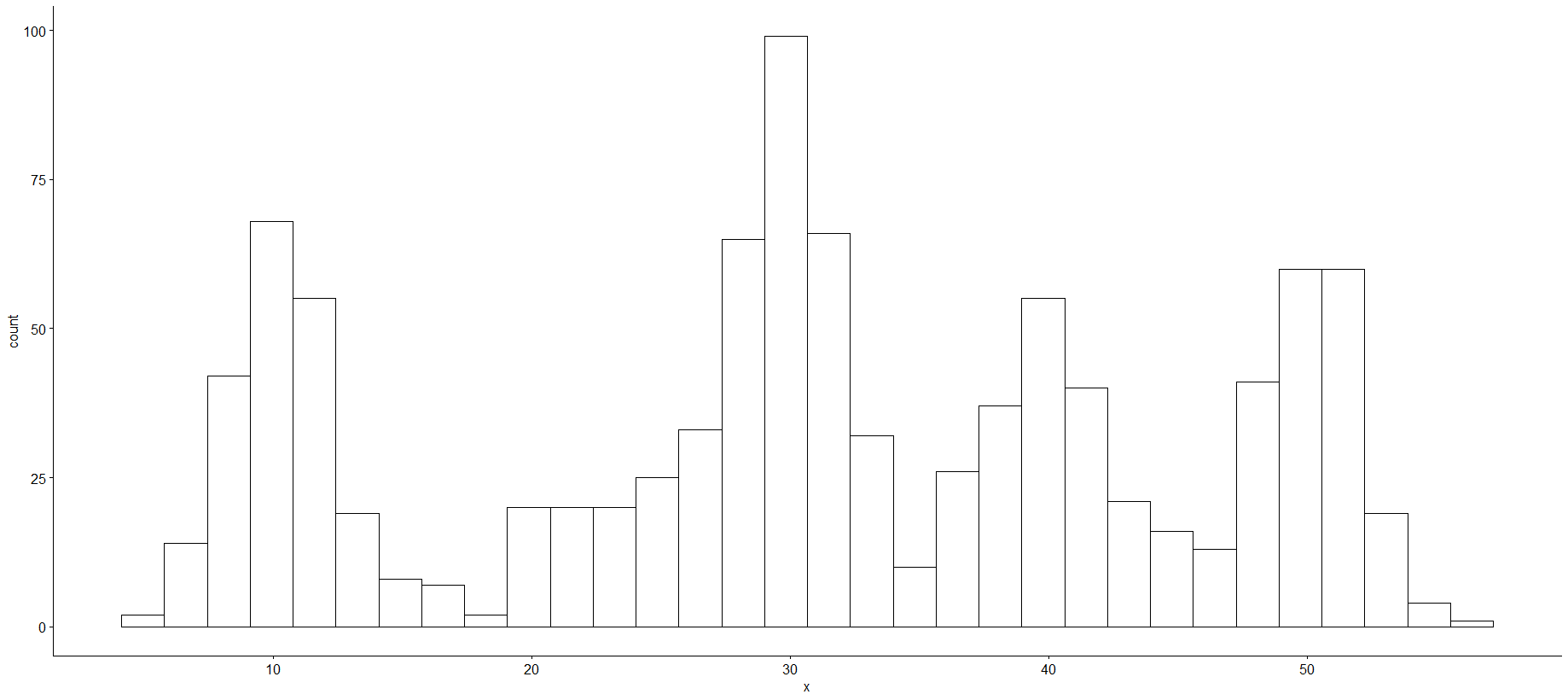
A mindennapokban vizsgált problémák esetében nem ismerjük a sokaságot, most azonban pont az a cél, hogy összehasonlítsuk a sokaságból kivett minták valós átlagainak eloszlását a minta alapján becsült megbízhatósági tartománnyal. Ezért véletlenszerű, de nem visszatevéses mintavétellel generáltam 100 000 darab 15-elemű mintát. A kivett minták átlagainak 95%-a 24,08 és 38,06 közé esik.
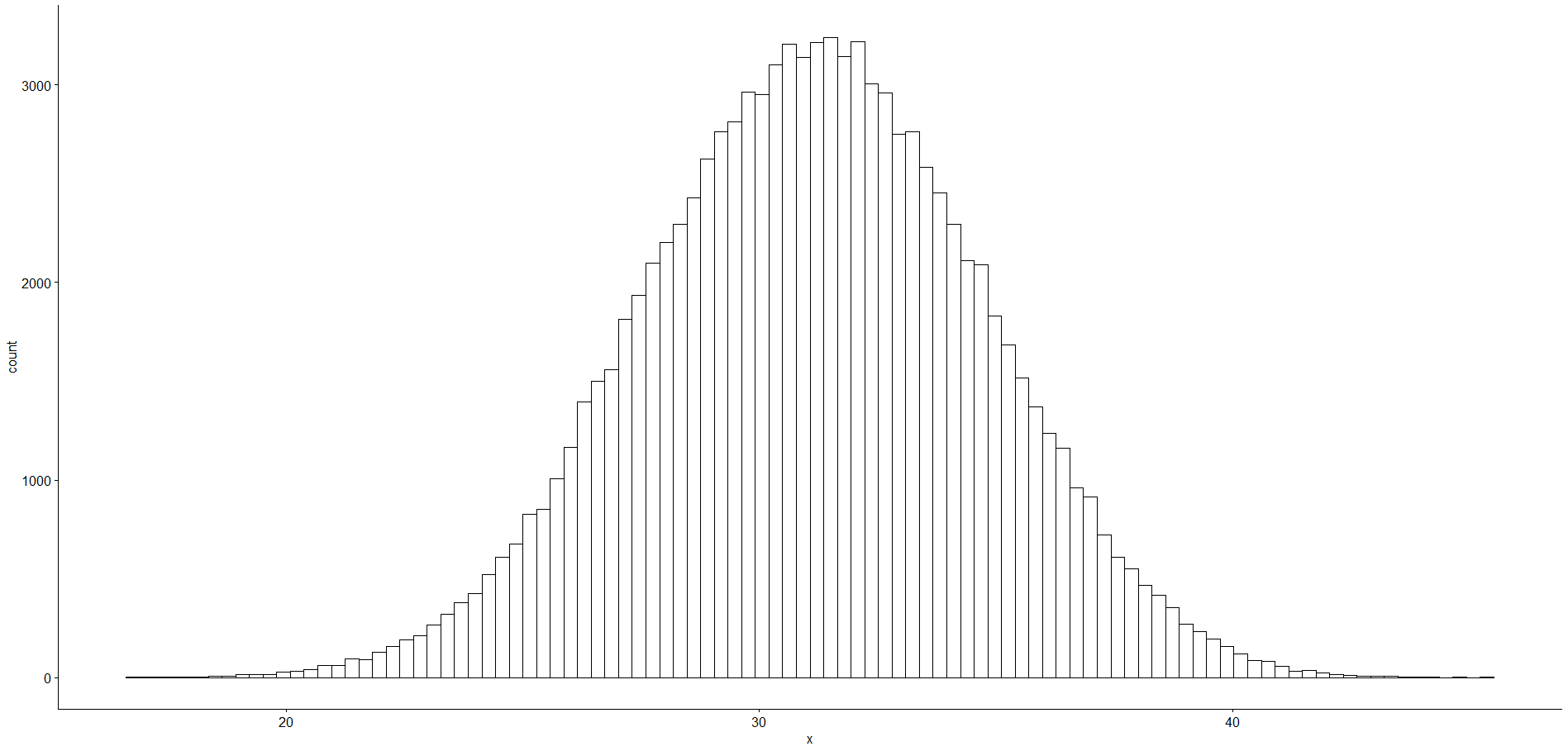
Akkor most válasszunk ki 15 számot véletlenszerűen a sokaságból:

Most érkeztünk el a vizsgálat legfontosabb pontjához. A minta elemeiből visszatevéses mintavétellel létrehoztam 100 000 darab mintát, majd kiszámoltam ezek átlagát és mediánját. Ezek szép nagy adattáblák, illetve vektorok lettek. A 100 000 darab minta átlagainak hisztogramja a következőképpen néz ki.
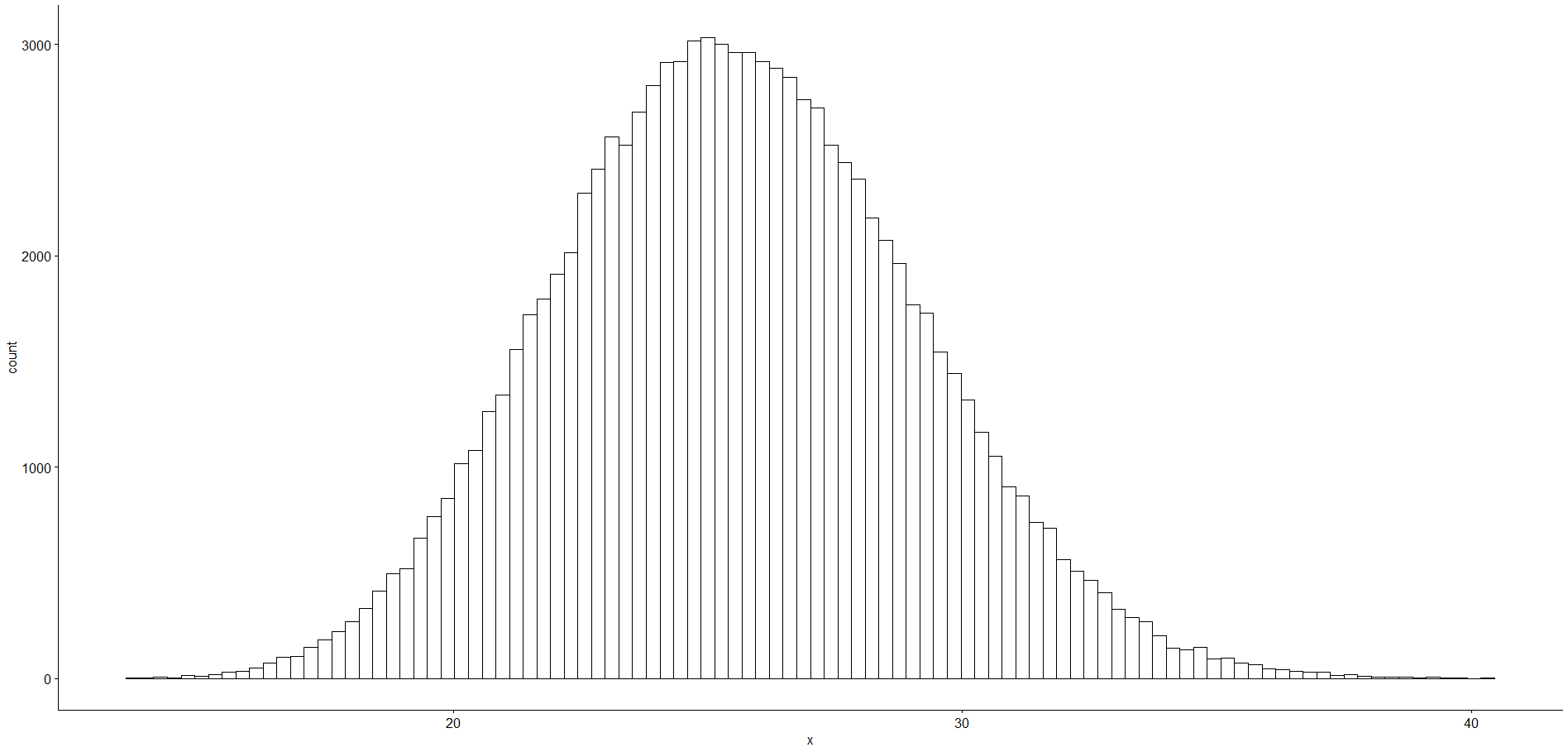
Utolsó lépésként kiszámoltam az x-tengelyen lévő értékeknek azt az alsó és felső határát, amelyek közé esik a 100 000 darab átlag 95%-a. Az így kapott alsó határ 18,95, a felső határ pedig 32,67.
Az így kapott határértékek természetesen nem ugyanazok, mint amit a sokaság alapján kaptunk. A sokaság elemeinek 95%-a 24,08 és 38,06 közé, a mintából generált bootstrap megbízhatósági tartomány viszont 18,95 és 32,67, Mindkét tartomány szélessége nagyjából azonos, de a minta alapján becsült megbízhatósági tartomány viszont körülbelül 5-tel kisebb értékeket mutat.
Nyilván fogadjuk el, hogy ez egy becslés, és hogy egy minta sohasem fogja tökéletesen visszaadni a sokaság tulajdonságait, amelyből kivették. Másrészt vegyük figyelembe, hogy a sokaságból kivett minta nem adhatja vissza teljeskörűen a sokaság tulajdonságait, ezért a becslés jósága erősen függ a minta tulajdonságaitól. Egy szélsőségesen kiválasztott minta esetén ez a különbség még nagyobb is lehet. Viszont figyelembe véve, hogy a sokaság alakja mennyire szabálytalan, a mintaszám pedig relatíve kicsi, az eredmény nem is olyan rossz!





