
Milyen jó, ha időnként találkozunk olyan elnevezésekkel a statisztikában, amelyeknek látszólag még értelme is van! Sajnos az ajánlóban emlegetett jackknife és bootstrapping módszerek esetében csak akkor értjük meg a névadás logikáját, ha megismerjük a kitalálásuk történetét is.
Először ismerjük meg az alapproblémát. Van nekünk egy remek tételünk, a Centrális Határeloszlás tétele (A nagy dobókocka kísérlet), amelyet remekül ki tudunk használni egy csomó esetben, amikor sokelemű mintákat veszünk ki egy ismeretlen eloszlású sokaságból és a minta alapján próbáljuk megbecsülni a sokaság átlagát. Csak sajnos az életben előforduló kutatnivaló eseteknek csak egy megadott hányadában áll fenn a fenti feltétel. Mi van akkor például, ha a megismerni kívánt sokaságról tudjuk, hogy aszimmetrikus. Vagy mit tegyünk akkor, amikor nem a sokaság átlagára, hanem a mediánjára, a varianciájára vagy a szórására vagyunk kíváncsiak? Ezekben az esetekben a Centrális Határeloszlás tétele vajmi kevés segítséget nyújt a feltett kérdések megválaszolásában.
Egy Maurice Quenouille nevű matematikus publikálta először azt az ötletet, hogy ha van egy n-elemű mintánk, akkor készítsünk abból (n-1) elemű mintákat úgy, hogy szisztematikusan eltávolítjuk a minta egy-egy elemét. Az ötletet később John Tukey, amerikai matematikus fejlesztette tovább, ezért is hívják Quenouille-Tukey jackknife-nak. Egy egyszerű példán bemutatva a dolgot, ha van egy négy elemű mintánk, amelynek az elemei az 1, 2, 3 és a 4, akkor ebből képezni tudunk 4 darab 3-elemű mintát, amelyek az {1, 2, 3}, az {1, 2, 4}, az {1, 3, 4} és a {2, 3, 4}. Ha kiszámítjuk a 4-elemű minta átlagát, akkor ezek megadják az adott jellemzőre vonatkozó mintaeloszlást. Például a fenti példa esetében a 3-elemű minták átlagainak átlaga jól közelíti a sokaság átlagát. A 4-elemű minta átlaga
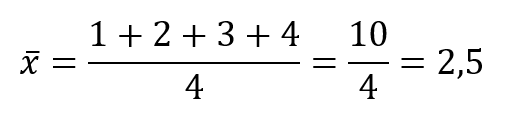
A négy darab 3-elemű minta átlagai a következők:
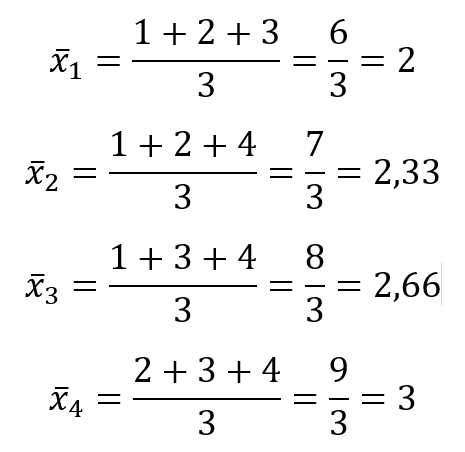
Ha kiszámítjuk a 4 darab mintaátlag átlagát, akkor a következőt kapjuk:
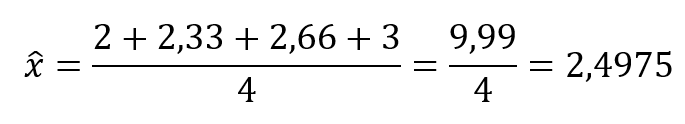
Vagyis a Centrális Határeloszlás tételéhez hasonlóan a mintaátlagok átlaga jól közelíti a sokaság szórását.
A sokaság varianciájának vagy szórásának becslése sem sokkal bonyolultabb:
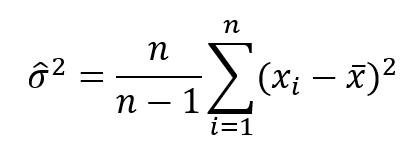
Ez a fenti példában a következőt jelenti:
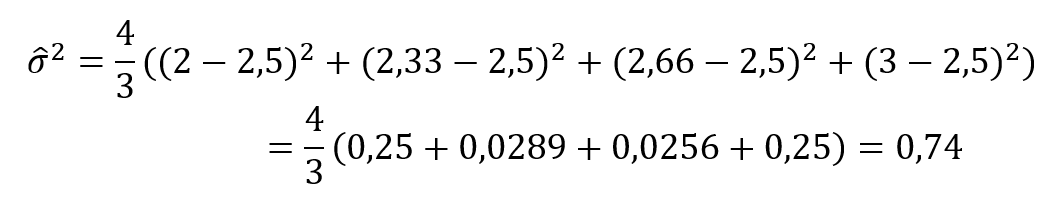
Ebből a sokaság szórásának becsült értéke
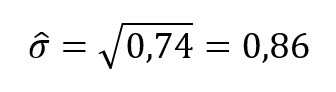
Ha az eredeti 4-elemű minta alapján kiszámítjuk a mintaeloszlás szórásának értékét, akkor az nem lesz túl messze a fenti becsléstől. A négyelemű minta varianciája
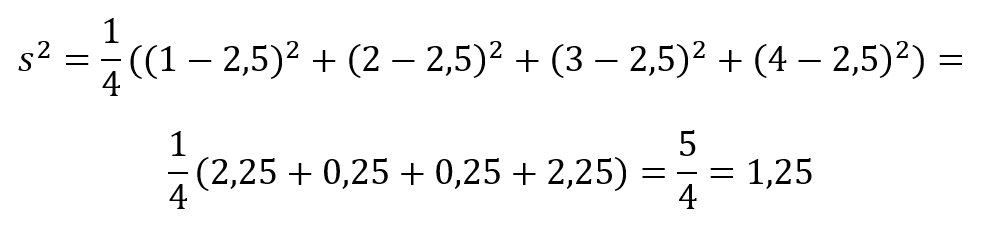
Ebből pedig a minta szórása
![]()
Ha ebből megbecsüljük a sokaság szórását a Centrális Határeloszlás tétele alapján, akkor
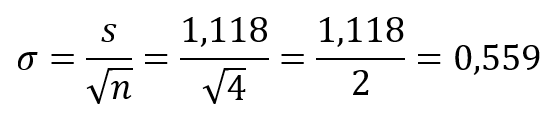
A jackknife algoritmus egyik komoly hátránya, hogy az átlag becslése esetében jól működik, de a medián (nem elég folytonos) vagy például a korrelációs együttható (nem lineáris) esetében sajnos nem. Emiatt is kapta a nevét. A "jackknife" kifejezés angolul bicskát jelent, amit akkoriban igen sok férfi hordott magánál. A bicska nem egy tökéletes eszköz, de egyszerű magadnál hordani és mindig kéznél van.
A bootstrap módszert Bradley Efron publikálta 1979-ben. A név a csizmákra varrott fülekre utal (lásd a képet a cikk elején), amelyek a csizmák felhúzását segítik és arra a helyzetre utal, amikor "kihúzod magad a bajból a csizmaszáradnál fogva". Előtte évekig dolgozott azon, hogy találjon egy olyan módszert, amely kevésbé szisztematikus, viszont jobban véletlenszerű, mint a kiinduló metódus. A bootstrapping lényege az, hogy a rendelkezésre álló n-elemű mintából nagyszámú n-elemű mintát veszünk ki. Ez így első olvasásra logikátlannak tűnik, de a titok a mintavétel módjában van, ugyanis a mintákat úgynevezett visszatevéses módszerrel választjuk ki, ami azt jelenti, hogy miután kivettünk egy mintaelemet a vizsgált mintából, utána visszatesszük azt a "kalapba", vagyis újra van esélyünk kihúzni azt. A fenti példánál maradva az {1, 2, 3, 4} mintából ki tudunk venni olyan mintákat is, mint az {1, 1, 2, 4}, vagy akár a {2, 2, 3, 2}.
Ezzel a módszerrel elegendően nagyszámú n-elemű mintát kivéve a minták tulajdonságait háromféle módon kezelhetjük:
- Kezelhetjük ugyanúgy, mintha a nagyszámú mintát a sokaságból vettük volna ki.
- Készíthetünk Monte-Carlo szimulációt az adatok alapján
- Kezelhetjük Taylor-kiterjesztésként.
Azóta inkább a bootstrapping módszer terjedt el és számos változata is született az idők folyamán, amelyek különféle speciális helyzetekben alkalmazhatók. A következőkben ki fogom próbálni a módszer hatásosságát egy valós példa alapján.
Források:
LaFontaine, Denise (2021) "The History of Bootstrapping: Tracing the Development of Resampling with
Replacement," The Mathematics Enthusiast: Vol. 18 : No. 1 , Article 8.
https://scholarworks.umt.edu/tme/vol18/iss1/8
Bradley Efron: Bootstrap methods: another look at the jackknife, The Annals of Statistics, 1979, Vol. 7, No. 1, 1-26
https://projecteuclid.org/journals/annals-of-statistics/volume-7/issue-1/Bootstrap-Methods-Another-Look-at-the-Jackknife/10.1214/aos/1176344552.full
S. Sawyer: Resampling Data: Using a Statistical Jackknife, Washington University — March 11, 2005
https://www.math.wustl.edu/~sawyer/handouts/Jackknife.pdf
Statistics by Jim: Introduction to Bootstrapping in Statistics with an Example
https://statisticsbyjim.com/hypothesis-testing/bootstrapping/





