Most vizsgáljuk meg közelebbről a sokaság és a minta kapcsolatát egy egyszerű példán keresztül. Tegyük fel, hogy van egy dobókockánk és végtelen türelmünk, hogy egymás után ötezer (!) alkalommal feldobjuk a kockánkat és minden egyes dobás után akkurátusan feljegyezzük a dobás eredményét. Tegyük ezt ráadásul úgy, hogy az eredményeket tízesével csoportokba rendezzük. Hogy miért tesszük mindezt? Azért, hogy létrehozzunk egy „sokaságot”. Ez a sokaság nem feltétlenül tökéletes, de az ötezer dobás már elegendően nagy ahhoz, hogy megfeleljen a célnak, tehát megközelítőleg szimuláljon egy sokaságot.

Természetesen én túlságosan lusta vagyok ahhoz, hogy ötezerszer feldobjak egy dobókockát, ezért egy táblázatkezelőt hívtam segítségül. Szerencsére a jól ismert táblázatkezelő programokban van véletlenszám generáló függvény, így az ötezer dobás eredményét pár perc alatt sikerült létrehoznom. Noha ezek a számok nem teljesen véletlen számok, de ez a közelítés most bőven megfelel a céljaimnak. A kapott táblázat 500 sorból és 10 oszlopból áll, és ennek a táblázatnak minden cellájában egy 1 és 6 közötti véletlenszerűen generált egész szám áll. Ezután még létrehoztam egy 11. oszlopot, aminek minden egyes cellája az adott sorban lévő 10 elemű minta átlagát tartalmazza.

Miután létrehoztam a „sokaságot”, először is kiszámoltam az ötezer darab egyedi érték átlagát és szórását. Azt kaptam, hogy az ötezer darab egyedi érték átlaga 3,5024, varianciája (a szórás négyzete) pedig 2,8446. Az átlagként kapott ~3,5 tulajdonképpen logikus is, hiszen a 3,5 pont félúton van a 3 és a 4 között, ami a dobókocka két középső száma. Nyilván, ha a dobókockának 7 oldala lenne, akkor a dobások várható értéke 4 lenne és nem 3,5. A varianciára kapott ~2,8 azt jelenti, hogy a dobások várható értéke valahol a 3,5 – 2,8 = 0,66 és a 3,5 + 2,8 = 6,35 között van. Persze a kicsit is szemfüles olvasó kiszúrja, hogy a dobókockával nem lehet 1-nél kisebbet, illetve 6-nál nagyobbat dobni, tehát az átlag várható értéke még szélsőséges esetekben sem lehet kisebb 1-nél, illetve nagyobb 6-nál. Ezek az átlag várható értékének természetes határai.

-------------------------------

Helyesbítés: Az előző bekezdésben bizony nem jól számoltam. Diszkrét adatsor esetében a sokaság szórását nem a szokásos képlettel számítjuk ki, hanem a következő módon:

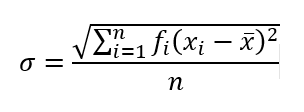
ahol fi azt jelöli, hogy az 1..6 számok közül melyik milyen gyakran fordul elő az n=5000 darabos adatsorban, xi az 1..6 számok szép sorjában, az x-felülvonás pedig az 5000 darab kockadobás átlaga, azaz 3,5024. Ha ezt így végig számoljuk, akkor a következőket kapjuk:

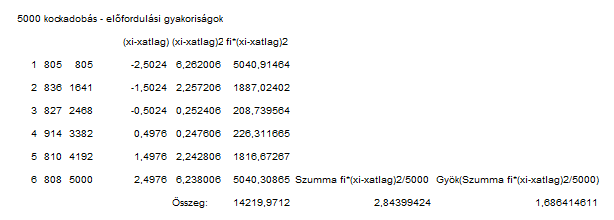
Így valóban 1,7 jön ki a szórásra, így a várható érték 3,5 - 1,7 = 1,8 és 3,5 + 1,7 = 5,2 lesz.

Elnézést a hibáért.

-------------------------------

És mit kapunk, ha megvizsgáljuk, hogy az ötezer szám között mennyiszer fordul elő az 1, a 2, a 3, a 4, az 5 vagy a 6? Szerencsére egy egyszerű függvény segítségével ezeket is pillanatok alatt meg tudom számolni és ábrázolni is tudom egy oszlopdiagramon:

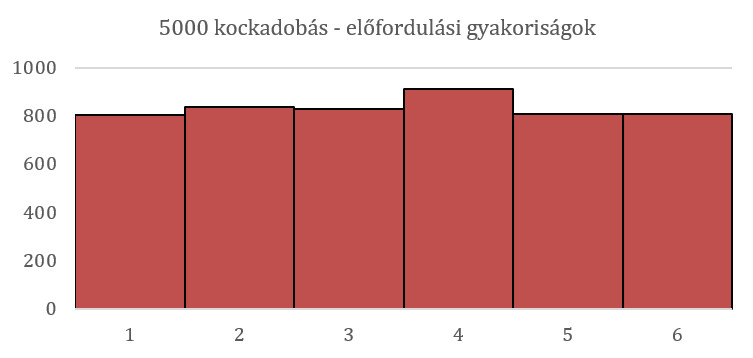Akkor most nézzük meg, mi a helyzet a 10 elemű minták átlagaival? Az átlagok vizsgálata azt mutatja, hogy ezek a számok már nem egész számok, hanem valós számok, tehát a mintaátlagok folytonosak ellentétben magukkal a mintákkal, amelyek a dobókocka jellegéből adódóan diszkrét értékeket vettek fel. Készítettem egy hasonló diagramot az 500 darab mintaátlag előfordulási gyakoriságairól.

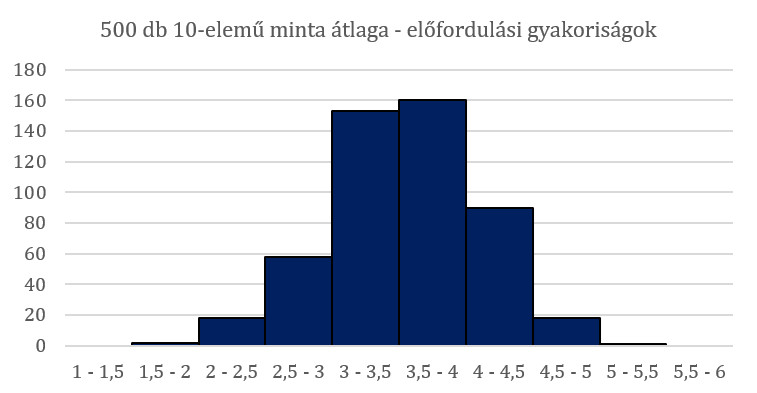Nocsak! Ennek a diagramnak teljesen más alakja van, mint az előzőnek. Ez hogyan történhetett? Lehetséges, hogy ha egy adatsorban a különböző értékek egyenlő arányban fordulnak elő, akkor az ezekből az adatokból képzett minták átlagai nem egyenlő arányban fordulnak elő? A fenti diagram legalábbis azt mutatja, hogy a mintaátlagok egészen széles tartományban szórnak, akadnak közöttük olyan minták is, amelyeknél a 10 eredmény átlaga 1,7 de olyan is akad, amelyiknek 5,3. A többség azonban 3 és 4 közé esik, és minél távolabb kerülünk a 3,5 körüli várható értéktől, annál ritkábban fordul elő olyan mintaátlag, amely az adott tartományba esik.

Nos, ez igaz és általánosabban is igazolható. Függetlenül attól, hogy egy adathalmaz egyes elemei milyen gyakorisággal fordulnak elő az adathalmazban a többi elemhez képest (tehát milyen a kockadobások egyes lehetséges kimeneteleinek eloszlása az adathalmazban), az adathalmaz elemeiből képzett minták átlagainak előfordulási gyakorisága mindig ugyanazt a jellegzetes mintázatot fogja követni, azaz a mintaátlagok előfordulási gyakorisága normál eloszlású lesz. Ezt hívjuk a Centrális Határeloszlás tételének.

Ez egy nagyon hasznos felfedezés, a későbbiekben ez a tétel még sokszor a hasznunkra lesz.

Viszont van itt még egy apróság, amivel foglalkoznunk kell. Jelen pillanatban ismerjük a sokaságot, hiszen tudatosan így rendeztük be a kísérletet. Tudjuk mennyi a sokaság várható értéke, azaz átlaga és ismerjük a varianciáját is. A valóságban viszont nem ismerjük a sokaságot, csak a sokaságból kivett minták alapján következtetünk arra, hogy a sokaságnak milyenek is lehetnek a tulajdonságai.

Tegyük fel, hogy nem 500, hanem csak 1 darab 10 elemű minta alapján szeretnénk valamit mondani a sokaság várható értékéről. De mi fog történni akkor, ha a 10 elemű mintánk átlaga éppenséggel 1,7 vagy mondjuk 5,3 lesz? Akkor azt fogjuk mondani, hogy a dobókocka dobások sokaságának várható értéke 1,7 vagy azt, hogy 5,3? A józan eszünk azt súgja, hogy ez nem lehet, de a 10 elemű minta átlaga ennyi, ez alapján nem mondhatjuk, hogy a sokaság átlaga 3,5! Mi lehet a gond?

Mi lenne, ha próbaképpen megnövelnénk a minták számát? Ha nem 10 elemű, hanem 50 vagy akár 100 elemű mintákat vizsgálnánk? Szerencsére nem igényel különösebb erőfeszítést megvizsgálni ezeket a variációkat is, lássuk mit kaptunk eredményül:

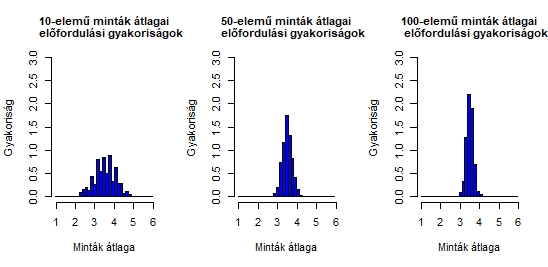
Három diagramot látunk, az első az 500 darab 10 elemű minta, a második a 100 darab 50 elemű minta, a harmadik pedig az 50 darab 100 elemű mintaátlagainak előfordulási gyakoriságát ábrázolja. A jobb átláthatóság kedvéért mindhárom esetet azonos csoportbeosztásokkal ábrázoltam az x-tengelyen. Jól látható, hogy minél több elemű minták átlagait vizsgáljuk, a mintaátlagok annál szűkebb tartományba fognak esni!

Tegyük fel, hogy be akarom bizonyítani, hogy ha a dobókockámmal ötezerszer dobnék, akkor az ötezer dobás eredményének várható értéke 2,8 lesz (ami persze nem igaz). Ha 10 elemű mintát veszek, akkor a fenti tapasztalatok alapján simán dobhatok 10 olyan számot, amelyeknek az átlaga 2,8 vagy annál kisebb. Vagyis van esélye annak, hogy noha a sokaságom szórása 3,5, a 10 elemű minta alapján bebizonyítom, hogy a sokaság szórása 2,8, azaz hibázok. Az 500 darab minta között 58 olyan minta található, amelynek átlaga kisebb, vagy megegyezik 2,8-cal, azaz több, mint 11% az esélye a hibázásnak.

Mi történik, ha egy 50 elemű minta alapján szeretném bebizonyítani ugyanezt? A második diagramból kiderül, hogy az esélyem a hibázásra sokkal kisebb, de még mindig lehetséges. A 100 darab 50 elemű minta között egyetlen olyan minta sincs, amelynek az átlaga kisebb vagy egyenlő lenne 2,8-cal. Viszont van két olyan minta, amelynek az átlaga 2,88, tehát közel van a 2,8-hoz. Egy 50 elemű minta esetében már nagyon kicsi lenne az esélye a hibának.

Egy 100 elemű minta esetében már a diagramon is jól látható, hogy egyetlen olyan minta sincs az 50 darab között, amely 2,9-nél kisebb lenne, tehát ebben az esetben a hibázás valószínűsége már tényleg majdnem nulla.
Milyen tanulságokat lehet levonni a fentiekből?

- Minél több elemű mintát veszünk ki a sokaságból, annál kisebb lesz a mintaátlagok szóródása, azaz annál pontosabban tudunk következtetni a sokaság tulajdonságaira. A centrális határeloszlás tételének második fele kimondja, hogy a mintaátlagok átlaga megegyezik az egyedi értékek átlagával, a mintaátlagok szórása pedig megegyezik az egyedi értékek szórásával, elosztva azt a mintaszám (jelen esetben 10, 50 vagy 100) négyzetgyökével.

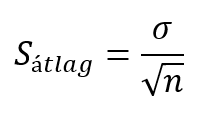
- Amikor egy minta tulajdonságai alapján szeretnénk következtetni a sokaság tulajdonságaira, akkor igen óvatosan kell eljárni, nehogy téves következtetésekre jussunk amiatt, hogy egy túl kevés elemből álló minta alapján próbáljuk meg bizonyítani a feltételezésünket.

FRISSÍTÉS:

A fenti bejegyzésen felbuzdulva Udvari Zsolt, a debreceni Bethlen Gábor Református Gimnázium matematika és fizika szakos tanára a saját weboldalán közzétette a fenti kísérlet R nyelven megírt programját is. Akit érdekel, innen letöltheti:

http://uzsolt.hu/edu/math/stat/190201_dobokocka.html

Köszönöm