A normál eloszlásról már volt szó dióhéjban (lásd itt és itt), de eddig nem nagyon mentem bele a részletekbe, inkább csak azt próbáltam tisztázni, hogy honnan származik és mivel magyarázható a létezése. Hogy őszinte legyek, hirtelen nem is tudom, hol kezdjek hozzá, annyi mindent kellene tisztázni ezzel kapcsolatban.
A normál eloszlásnak van néhány érdekes tulajdonsága, amit mindenképpen meg kell említenem, mielőtt belevágok a címben megadott témába. A normál eloszlás sűrűségfüggvényének képlete a következő:
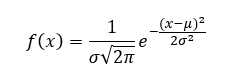
Ha jól megnézzük ezt a bonyolult függvényképletet, akkor azt látjuk, hogy maga az alapfüggvény így néz ki:
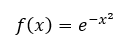
Tehát ez egy exponenciális függvény, amely esetében az 'e' az Euler-féle szám, amelyet a természetes alapú logaritmusok esetében is alkalmazunk. Az, hogy a kitevőben x helyett x-négyzet van, az biztosítja, hogy a függvény szimmetrikus legyen, hiszen a negatív számok négyzete pozitív. Az, hogy a kitevőben nem x-négyzet, hanem mínusz x-négyzet szerepel, az pedig arra szolgál, hogy minél nagyobb x értéke, annál kisebb legyen a függvény értéke, hiszen
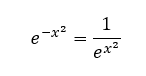
E szerint minél nagyobb x értéke, annál nagyobb számmal fogjuk elosztani az 1-et, tehát a függvény értéke annál kisebb lesz. Ha ezt a függvényt ábrázolom a -4 és +4 közötti tartományban, akkor a következő grafikont kapom:
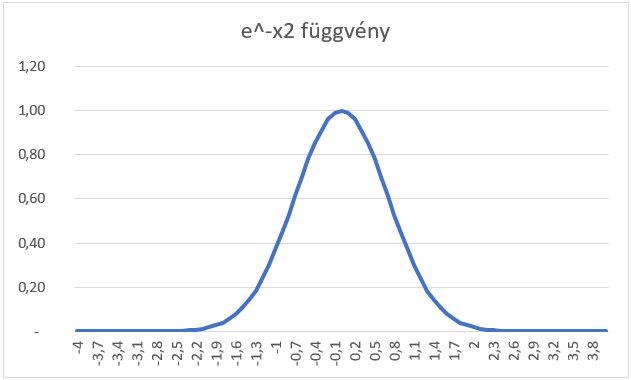
Tehát a normál eloszlás jellegzetes haranggörbe alakját az alapfüggvény adja meg. Az

egy korrekciós tényező, amely azért szükséges, hogy a sűrűségfüggvény görbe alatti területe, azaz a függvény integráltja 1 legyen. Ez is logikusnak tűnik, hiszen a sűrűségfüggvény görbe alatti területének le kell fednie a teljes esemény teret, amely definíció szerint 1 (lásd itt – valószínűségi eloszlásokról I.), tehát a görbe alatti területnek 1-nek kell lennie. Az így korrigált függvény így néz ki:
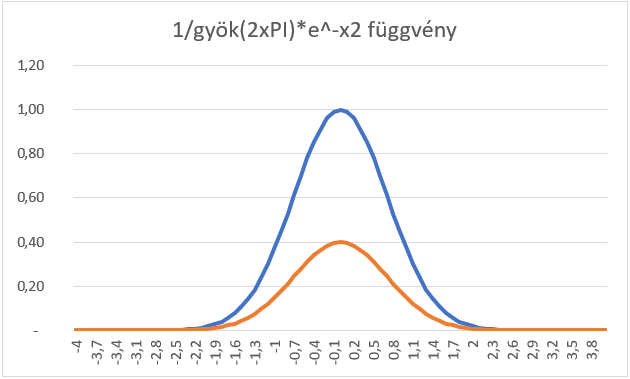
Mivel a fenti állandó értéke 0,398, így az eredmény tulajdonképpen annyi, mintha minden egyes függvényértéket megszoroznánk 0,4-gyel. Egy megadott sokaság esetében µ és σ értéke ugyanúgy állandók, amelyek módosítják a függvénygörbe alakját.
Ha összehasonlítunk olyan sokaságokat, amelyeknek az átlaga és szórása különbözik, akkor azt tapasztaljuk, hogy a különböző átlagok és szórások különféle függvény alakzatokat eredményeznek. Az átlag megváltozása eltologatja a görbe helyzetét az x-tengely mentén.
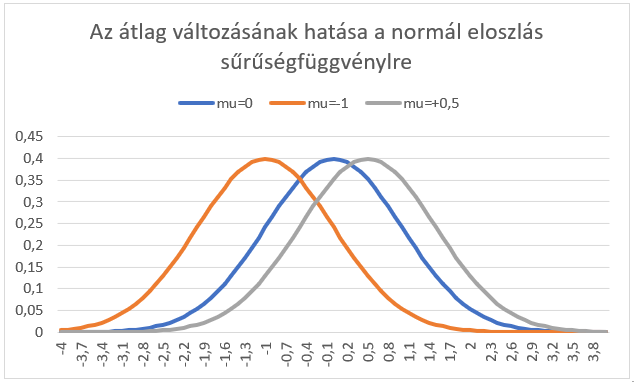
A szórás nagysága pedig a görbe szélességét és magasságát is befolyásolja, hiszen mivel a görbe alatti területnek mindig 1-nek kell lennie: ezért, ha a görbe keskenyebb, a görbe legmagasabb pontja nagyobb értéket vesz fel, ha viszont a görbe szélesebb, akkor a görbe legmagasabb pontja alacsonyabban lesz.
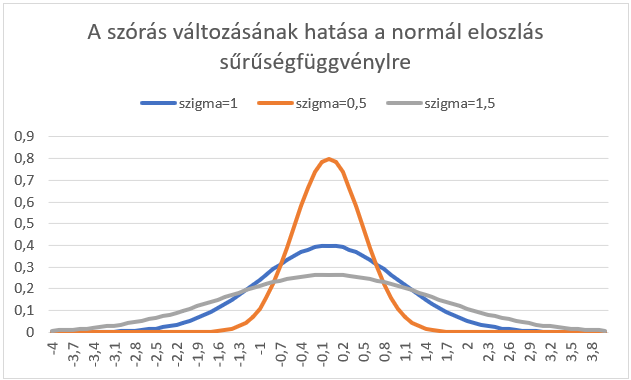
Ez alapján kijelenthető, hogy mivel a sokaságok átlagai és szórásai is végtelen számú értéket vehetnek fel, ezért végtelen számú normál eloszlás létezik a világban. amíg nem léteztek számítógépek, addig ezek kezelése nagyon hosszadalmas és munkaigényes lett volna. Képzeljétek el, ha a fentebb említett bonyolult képlet értékét kellett volna kiszámítani papíron, zsebszámológép nélkül. Kellett egy eredeti gondolat, hogyan lehet leegyszerűsíteni a számítást. Végül megszületett az ötlet, hogy legyen kijelölve egy bizonyos átlag – szórás kombináció és legyen minden egyéb normál eloszlás kombináció erre az egy közös normál eloszlásra visszavezetve. Ez a bizonyos kiemelt jelentőségű normál eloszlás az lett, amelynek az átlaga 0, a szórása pedig 1, ezt nevezték el standard normál eloszlásnak. Az, hogy miért pont ez az átlag – szórás kombináció nyert, annak több gyakorlati oka is van.
A legfontosabb ezek közül az, hogy ha behelyettesítjük a µ=0-t és a σ=1-et a normál eloszlás fenti képletébe, akkor az nagymértékben leegyszerűsödik, így:
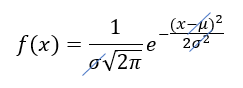
azaz
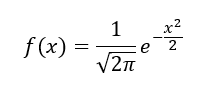
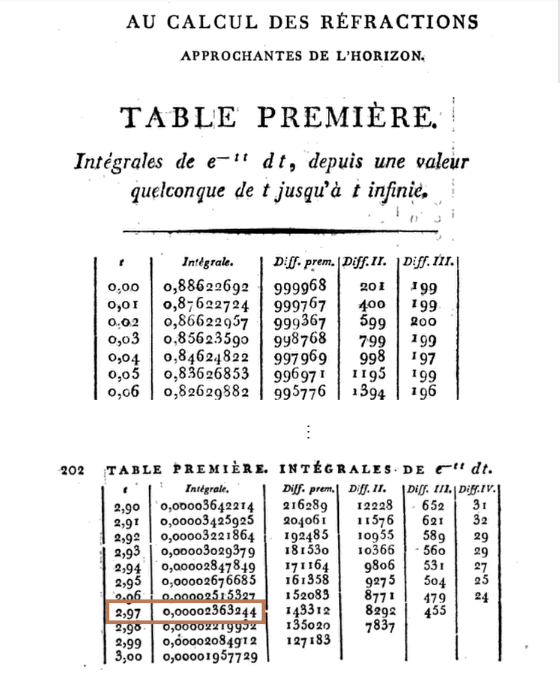
Mivel megegyeztünk abban, hogy a képlet elején lévő tört értéke mindig állandó, illetve az ’e’ kitevőjében lévő tört így sokkal egyszerűbben kiszámítható, így már létre lehetett hozni egy olyan táblázatot, amelyből egyszerűen csak ki kellett keresni az adott számhoz tartozó függvényértéket. Ilyen táblázatok jelenleg is léteznek, ennek bemutatása egy másik bejegyzés tárgya lesz.
Egy probléma viszont mégiscsak maradt: Hogyan jutunk el egy bármilyen normál eloszlástól a standard normál eloszlásig? A válasz ismét csak relatíve egyszerű: Fentebb tisztáztuk, hogy az átlagnak és a szórásnak milyen hatása van a függvénygörbe alakjára. Ha tehát mondjuk a mi normál eloszlásunk átlaga 3, és keressük a mi eloszlásunk esetében az x = 2-höz tartozó valószínűség értéket, akkor egész egyszerűen kivonjuk x-ből a mi eloszlásunk µ értékét, azaz 3-at, így megkapjuk, hogy a standard normál eloszlás szerint mennyi lenne x értéke (jelen esetben -1).
Ez persze akkor igaz, ha a mi normál eloszlásunk szórása 1. De mit tegyünk akkor, ha tegyük fel a mi normál eloszlásunk szórása 2, hiszen akkor a mi normál eloszlásunk kétszer szélesebb és laposabb, mint a standard normál eloszlás? Ez esetben osszuk el az x-µ különbséget a mi normál eloszlásunk szórásával, azaz 2-vel, hiszen így a kapott érték így adaptálódik a standard normál eloszláshoz.
Összefoglalva az eljárás az, hogy ha egy bármilyen normál eloszlás esetében egy bármilyen x értékhez ki akarjuk keresni azt az x’ értéket, amely pont ennek az x értéknek felel meg a standard normál eloszlás szerint, akkor az

képlettel ki kell számolnunk x’ értékét. Ezután már csak egy standard normál eloszlás táblázat kell, amelyből ki lehet keresni az x’ értékhez tartozó valószínűséget, amely pontosan meg fog egyezni a mi eredeti x értékünkhöz tartozó valószínűséggel. Ehhez már csak az kell, hogy a rendelkezésünkre álljon a megfelelő táblázat – például egy négyjegyű függvénytáblában – és azt is tudjuk, hogyan kell azt használni.
Utolsó megjegyzésként annyi, hogy a modern számítógépek és szoftverek korában már nincs igazán létjogosultsága ennek a módszernek, hiszen bármilyen táblázatkezelő programban van olyan függvény, amely bármilyen átlag – szórás kombinációra kiszámítja egy x értékhez tartozó valószínűség értékét, így jobban megérné ezt megtanítani, mint a standardizálással foglalkozni. Persze, ha csak papír, ceruza – netalán számológép - és persze legnagyobb szerencsénkre egy négyjegyű függvénytábla is a rendelkezésünkre áll, úgy a standardizálás is remekül alkalmazható.





