Ha törzsolvasója vagy a blognak, akkor talán még emlékszel a kétmintás t-próbára (Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba), amelynek segítségével el tudtuk dönteni, hogy két minta átlaga megegyezik-e egymással. A t-teszt jól működik két minta esetében, de mit csináljunk akkor, ha nem kettő, hanem három, négy vagy akár több mintát akarunk összehasonlítani? Ha t-próbát alkalmaznánk, akkor a mintákat egyenként kellene összehasonlítanunk egymással, azaz öt minta esetében mondjuk az első mintát össze kellene hasonlítana a másodikkal, a harmadikkal, a negyedikkel és az ötödikkel is. A második mintát még ezen felül össze kell hasonlítani a harmadikkal a negyedikkel és az ötödikkel is. Ha végig megyünk ezen a vonalon, akkor összesen 4+3+2+1, azaz 10 kétmintás t-próbát kellene elvégeznünk az öt minta teljeskörű vizsgálatához. Ehhez nyújt segítséget az úgynevezett egytényezős varianciaanalízis (vagy F-próba, vagy F-teszt, vagy F-statisztika, vagy F-táblázat, vagy One-way ANOVA, vagy ahogy tetszik).

Az érthetőség kedvéért ismét egy nagyon egyszerű adatsort fogok alkalmazni az F-próba táblázat kiszámításához, hogy jól követhető legyen. Tegyük fel, hogy három különböző csoport vagy módszer esetében vizsgáljuk ugyanazt a folytonos jellemzőt és arra vagyunk kíváncsiak, hogy a három csoport eredményeinek átlaga azonos-e vagy sem.

Az adathalmaz a következő:

Az első megfigyelés az, hogy ebben az esetben sem fontos az, hogy az egyes csoportoknak ugyanannyi eleme legyen, ez nagy könnyebbség lehet adott esetben.

Folytatásként számoljuk ki a három csoport átlagát:

Amint az látható, a három csoport átlaga eltér egymástól, de azért fel szeretném hívni a figyelmet arra, hogy noha az A csoport átlaga 4, van benne egy 7-es érték is; illetve, hogy noha a B csoport átlaga 6, illetve a C csoport átlaga 7, mindkét csoportban van egy-egy 4-es érték is! Vagyis annak ellenére, hogy a három csoport átlaga nem egyezik meg, elképzelhető, hogy azonos sokaságból származnak!

Most pedig számítsuk ki a nagyátlagot, amely az összes csoport összes elemének az átlaga (tehát nem a három csoport átlagának az átlaga!):

A nagyátlag adja meg azt a bázist, amelyhez viszonyítjuk az egyes csoportok átlagait külön-külön. Ennek megfelelően számoljuk is ki az egyes csoportok átlagainak különbségét a nagyátlagtól:

És akkor itt most álljunk meg egy pillanatra és tisztázzunk két egyszerű fogalmat, a csoportok közötti (between) és a csoportokon belüli (within) szóródást.

A csoportok közötti (between) varianciát a csoportok átlagai és a nagyátlag alapján számítjuk ki:

Ezzel szemben a csoportokon belüli (within) varianciákat a csoportok elemei és a csoportátlagok közötti eltérések határozzák meg.

Remélem a számítások alapján érthető a különbség a csoportok közötti és a csoportokon belüli varianciák között. Viszont az egyszempontos varianciaanalízis nem a varianciákkal, hanem a négyzetek területével (Sum of Squares – SS) számol, amelyek tulajdonképpen nem mások, mint a fent kiszámított szórásnégyzetek számlálói! A teszt célja pedig tulajdonképpen nem más, minthogy összehasonlítsa a csoportok közötti varianciák alapján kiszámolt négyzetek területét a csoportokon belüli varianciák alapján kiszámolt négyzetek összterületével. Az átláthatóság kedvéért ezt a műveletsort egy megadott formátumú táblázatba szoktuk rendezni, amely a következőképpen néz ki:

Ez a táblázat így elsőre egy kicsit titokzatosan néz ki (és akkor még finoman fejeztem ki magam), de most szépen sorban elmagyarázom az egyes címkék jelentését, majd kiszámoljuk a teszt eredményeit, és remélhetőleg a végére minden kitisztul.

Kezdjük a bal felső sarokban. A ’Source’ kifejezés forrást jelent, azaz ebben az oszlopban vannak az egyes varianciák forrásainak megnevezései. A ’between’ és a ’within’ kifejezések a már fent ismertetett csoportok közötti, illetve csoportokon belüli varianciákat jelölik, a ’Total’ kifejezés, pedig a teljes varianciát jelenti. Azaz a nyers adatok összegzett szórásnégyzetét két tényezőre bontjuk fel, a csoportok közötti, illetve a csoportokon belüli szórásnégyzetekre.

A második oszlop fejlécében lévő ’df’ kifejezés már esetleg ismerős lehet, ez az a bizonyos „szabadsági fokok száma”, azaz „degrees of freedom”, amelyről már korábban esett szó. Jelen esetben is ez adja meg azt, hogy hány függő, illetve független változónk van. A csoportok közötti varianciák esetében – mivel három csoportunk van - ez most 3-1, azaz 2. Általánosabban fogalmazva a csoportok közötti varianciák esetében a szabadsági fokok száma mindig eggyel kevesebb a csoportok számánál.

A teljes variancia esetében (Total) a szabadsági fokok száma ismét könnyen értelmezhető, mert a teljes variancia kiszámításához az összes csoport összes elemét felhasználjuk, így a ’Total’ sorhoz tartozó szabadsági fokok száma az összes adat száma – 1. Ez esetben az A, a B és a C csoportban összesen 12 darab adatunk van, így a Total szabadsági fokok száma 12 – 1 = 11 lesz.

A csoportokon belüli variancia esetében a szabadsági fokok száma a Total és a Between sorokban lévő szabadsági fokok különbségeként adódik. Vagyis a mi esetünkben ez 11 – 2 = 9 lesz. Az ANOVA táblázat jelenleg így néz ki:

A folytatásban ki kell számolnunk „a négyzetek területeit”, azaz a ’Sum of Squares’ (SS) értékeit. A csoportok közötti SS értékét úgy kapjuk meg, ha összeadjuk a fentebb kiszámolt csoportok közötti varianciák számlálóit. Viszont nem almát az almával hasonlítanánk, ha az így kapott négyzetek területét nem szoroznánk meg az egyes csoportokban lévő elemek számával, hiszen – ahogy azt majd látni fogjuk – ott minden csoportban ni-szer annyi négyzet területét vesszük figyelembe, mint a csoportok közötti ’Sum of Squares’ esetében.

A csoportokon belüli SS kiszámítása esetében szimplán összegezzük a csoportok egyes elemei és a csoportátlagok segítségével kiszámolt négyzetek területeit.

Természetesen az SSWithin értéke a három csoport SSWithin értékeinek az összege.

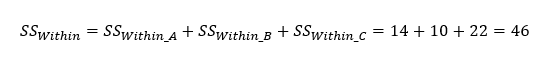
A teljes ’Sum of Squares’ pedig úgy adódik, hogy összegezzük a három csoport mind a 12 elemének a nagyátlagtól való távolságait, illetve az ezek alapján adódó négyzetek területeit. Az átláthatóság kedvéért ezt most táblázatos formában készítettem el.

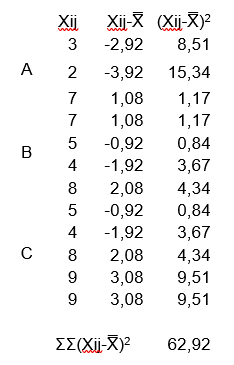
Így az ANOVA táblázat második oszlopa is kész lett.

Az MS oszlop elnevezése a ’Mean Square’ kifejezést takarja, ami annyit jelent, hogy amíg az SS oszlopban a különféle négyzetek területeinek összegeit szerepeltettük, itt ezeket – legalábbis a ’Between’ és a ’Within’ sorok esetében ezeket arányosítjuk az egyes sorokra eső szabadsági fokok számával, vagyis a négyzetek összegéből most számolunk igazából varianciát, hiszen az SS értékeket el fogjuk osztani a szabadsági fokok számával:

Az F-táblázatunk így újabb oszloppal bővült.

Már csak két értéket kell megkanunk a próba elvégzéséhez. Az F értéke tulajdonképpen a két MS érték hányadosa. Most viszont szükségem lesz a hitedre, hogy ne kelljen belemenni az F-eloszlás részleteibe. Arra kérlek, hogy HIDD EL(!), hogy két variancia hányadosának eloszlása egy bizonyos F-eloszlást követ, vagyis hasonlóan lehet használni az F-eloszlást ebben az esetben, mint a t-eloszlást vagy a normál eloszlást más esetekben, amelyekről már korábban beszéltünk.

Ahogy azt fentebb említettem, a kiszámított F érétke tulajdonképpen két variancia hányadosa, így F is az F-eloszlást fogja követni, azaz remekül fel tudjuk használni egy hipotézis ellenőrzésére. Szóval számoljuk ki, hogy mennyi F értéke.

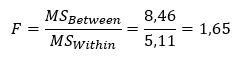
Nos, ahogy megszokhattuk, ez önmagában még semmit sem mond, a hipotézisünk igazolásához meg kellene határoznunk egy Fkrit határértéket, amellyel a kapott F értékünket össze tudjuk hasonlítani.

Ja – by the way – mi is a nullhipotézisünk ebben az esetben? Mert ezt nem tisztáztuk az elején. A nullhipotézisünk az, hogy a három csoport ugyanabból a sokaságból származik, az ellenhipotézis pedig az, hogy a három csoport közül valamelyik nem ugyanannak a sokaságnak a tagja, mint a többi. Vagyis szerencsés esetben csak azt tudjuk igazolni, hogy mindegyik minta ugyanabból a sokaságból származik. Ha viszont ezt nem tudjuk bizonyítani, akkor viszont a teszt alapján nem fogjuk tudni eldönteni, hogy melyik sokaság nem illik bele a képbe, illetve azt sem tudjuk majd igazolni, ha esetleg mindhárom csoport más és más sokaságokból származik. Így jártunk!

Akkor most találjuk ki, hogy mennyi az Fkrit határérték.  Ehhez ismét fel kell ütnünk egy még olvasható F-eloszlás táblázatot, amely tartalmazza az F-eloszlásnak legalább a különféle megbízhatósági szintekhez és szabadsági fokokhoz tartozó határértékeit.

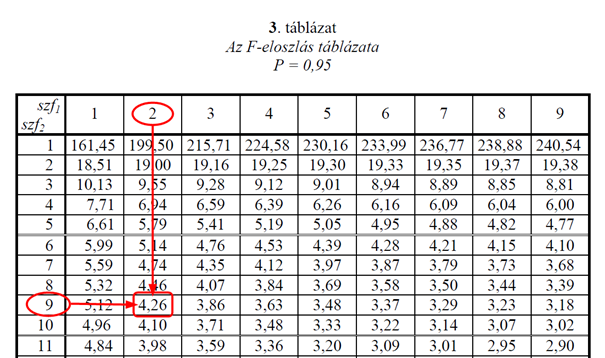
Jelen esetben nekem egy olyan táblázatom van, amely minden egyes megbízhatósági szinthez (95%, 97,5%, 99%) külön táblázatban tartalmazza a kritikus F értékeket. Ez azért szükséges, mert a kritikus F érték nem egy, hanem két szabadsági foktól függ: A számlálóétól és a nevezőétől. A táblázatot úgy olvassuk, hogy az oszlopok (szf1) jelentik a számláló, a sorok (szf2) pedig a nevező szabadsági fokát jelentik. Így megkapjuk, hogy esetünkben az Fkrit határérték 4,26. Így komplett lett az F-táblázatunk.

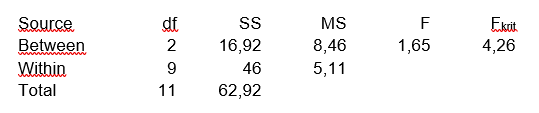
Mivel a kapott F érték kisebb, mint az Fkrit határérték, ezért a nullhipotézisünket 95%-os megbízhatósági szinten elfogadjuk, azaz a három csoport elemei 95%-os valószínűséggel ugyanabból a sokaságból származnak.

Noha maradt néhány apró részlet, amelyet még esetleg ki lehetett volna jobban is bontani a még mélyebb érthetőség kedvéért, azért úgy gondolom, hogy sikerült a témához mérten relatíve érthető módon elmagyarázni ezt a fontos tesztet, amelyet egyébként egészen sok helyen alkalmaznak a statisztikában, például a lineáris regresszió elemzés során is, ezt majd később látni fogjuk. Remélem, hogy az egyszerű példa segített a számítások követésében és végül is kiderült, hogy mi is hajtja a gépezetet…