A középérték mérőszámok esetében már volt szó a mediánról, amely az adatsor középső eleme, vagy a két középső elem átlaga. Ezzel az erővel tovább is szeletelhetjük az adatsorunkat, mondjuk négyfelé, ötfelé vagy akár tízfelé.
Én leginkább négyfelé szoktam szeletelni. A szeletelés azt jelenti, hogy nem kettő, hanem négy egyenlő részre bontom az adatsort úgy, hogy a medián meghatározásához hasonlóan (lásd itt) először sorba rendezem az adatsort, majd kiválasztom az adatsor legkisebb értékét, majd a negyedénél, a felénél, a háromnegyedénél lévő értéket (vagy az ott lévő két érték átlagát), végül az adatsor legnagyobb értékét. Nézzük meg ezt egy példán:
Vegyük a következő adatsort:
1 ; 3 ; 0 ; 3 ; 26 ; 2 ; 7 ; 4 ; 0 ; 2 ; 3 ; 3 ; 6 ; 3
Sorba rendezem az adatokat növekvő sorrendbe:
0 ; 0 ; 1 ; 2 ; 2 ; 3 ; 3 ; 3 ; 3 ; 3 ; 4 ; 6 ; 7 ; 26
Amint azt a fenti videóból kiderült, a medián értéke 3, mert az adatsor két középső eleme 3. Akkor most összeszedem a többit is.
Az adatsor legkisebb eleme 0.
Az első quartilis (Q1) értéke 2, mert ez az adatsor negyedik eleme. Miért a negyedik? Mert az adatsor 14 elemből áll. Ezt két darab 7 elemű részre lehet bontani és az alsó hét elem középső eleme a negyedik elem.
A harmadik quartilis (Q3) értéke 4, mert a felső hét elem közepe a tizedik elem.
Az adatsor legnagyobb értéke 26.
Összefoglalva:
0% 25% 50% 75% 100%
0 2 3 4 26
Mire jó ez nekünk? Több dologra is:
- A quartilisek segítségével tudjuk megrajzolni az adatsor doboz diagramját (boxplot), amelynek jellemző vonalait a quartilisek adják. A doboz rövidebb oldalainak a helyét a Q1 és a Q3 quartilisek adják meg, a középső vonalat a medián vagy Q2 quartilis határozza meg, a dobozból kiálló vonalak vége pedig az adatsor minimumát és maximumát mutatja meg. Ez egy tömör és praktikus ábrázolási mód, amelynek előnyeit leginkább ott élvezhetjük, amikor több különféle adatsort hasonlítunk össze.
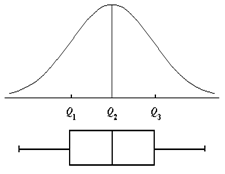
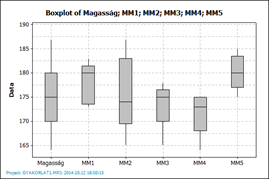
- A quartilisek segítségével lehet egyértelműen megállapítani, hogy az adatsor valamely értéke vagy értékei kieső értékek-e. A statisztikai programok kiszámítanak egy tartományt a quartilisek alapján: az ebbe a tartományba eső értékeket a szoftver az adatsor szerves részeként ábrázolja, a kieső értékeket viszont egy ponttal vagy csillaggal jelöli. Az előzőleg vizsgált adatsor dobozdiagramja a következőképpen néz ki:

Ez az R-ben készített dobozdiagram szinte szabályos alakot mutat, de a 26-ot a program egy különálló pontként ábrázolja. A statisztikai programok többsége a kieső értékek tartományát a következő módon határozza meg:
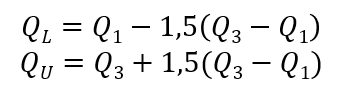
Tehát a programok veszik az adatsor középső tartományát (Q3-Q1) és ennek a másfélszeresét vonják ki a Q1-ből és adják hozzá a Q3-hoz.
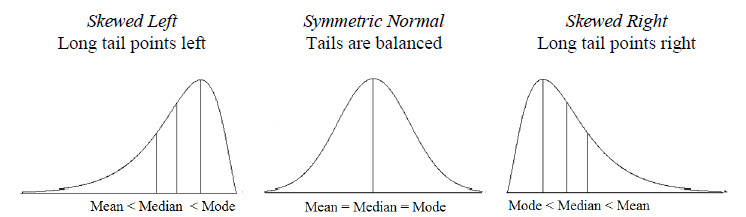
- A quartilisek harmadik alkalmazási területe az adatsorok sűrűségi eloszlása esetében az úgynevezett ferdeség vagy aszimmetria (skewness) becslése. Ez az úgynevezett Bowley-ferdeségi együttható (Bowley skewness coefficient). Ez azt mutatja meg, hogy az adatsor sűrűség hisztogramja mennyire szimmetrikus. Mivel tudjuk, hogy a normál eloszlás szimmetrikus eloszlás, amelynek az esetében az átlag, a medián és a mód egybeesik, ennek az együtthatónak az értéke utalhat arra, hogy az adatsor normál eloszlású-e vagy sem. Persze vannak erre már kifinomultabb módszerek is, de ez az együttható egyszerűen meghatározható és jól érthető.

Forrás: David P. Doane – Lori E. Seweard: Measuring Skewness: A Forgotten Statistic? – Journal of Statistics Education Volume 19, Number 2(2011) - http://jse.amstat.org/v19n2/doane.pdf
A Bowley-féle ferdeségi együtthatót a következő módon számolhatjuk ki:
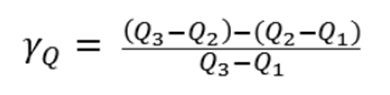

A grafikus ábrázolás alapján jól látható, hogy ha a Q3-Q2 megegyezik a Q2-Q1-el, azaz az adatsor közepe szimmetrikus, akkor a ferdeségi együttható értéke 0 lesz. Minél kevésbé szimmetrikus az adatsor, annál nagyobb lesz a ferdeségi együttható értéke. Természetesen önmagában ennek az egy mutatónak az alapján nem dönthető el egyértelműen, hogy az adatsor normál eloszlású-e vagy sem, de több más együttható együttes megfelelősége alapján már esetleg tudunk gyanakodni, hogy a feltételezés fennáll.





