Egy korábbi fejezetben már tárgyaltam azt a helyzetet, amikor két változó egymáshoz képesti kapcsolatát vizsgáljuk, konkrétan azt, hogy a két változó mennyire függ egymástól, azaz az egyik változó értékei mennyire határozzák meg a másikét és fordítva (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?). Az is hasznos információ lehet, ha két változó között nincs semmiféle kapcsolat, de most induljunk el a másik irányba, amikor a két változó között tényleg felfedezhető valamilyen kapcsolat. Ilyenkor mindig elkezd viszketni az ember tenyere, hogy ha már bizonyíték van arra, hogy a két dolog hat egymásra, akkor határozzuk meg, hogy milyen módon írható le ez a kapcsolat a matematika általánosabb nyelvén. Ha ezt a kapcsolatot valahogyan le tudnánk írni, azaz ha például meg tudnánk adni annak a függvénynek a képletét, amely ezt a kapcsolatot elég jól jellemzi, akkor akár a két változó jövőbeni értékeit is meg tudnánk határozni egymás függvényében, azaz a jövőbelátó varázsgömb kerülne a kezünkbe. Nekünk viszont csak adataink vannak, meg egy rakás pont egy diagramon, ebből kellene kifőzni valamit.

De ne szaladjunk ennyire előre, mert ez azért ennyire nem egyszerű dolog. Emiatt is kell több részre bontanom a lineáris regresszió elemzés ismertetését, hiszen elég sok dolgot kell megérteni és elképzelni magunk előtt ahhoz, hogy ezt a módszert helyesen és hatékonyan tudjuk alkalmazni.

Először is tisztázzuk azt, hogy regresszió elemzés nagyon sokféle létezik és a következő írásokkal csak a történet felszínét kapargatom, de valahol mégiscsak el kell kezdeni. A legeslegegyszerűbb ilyen elemzés az egyszerű egyváltozós lineáris regresszió, amely feltételezi, hogy a két változó között valamilyen lineáris kapcsolat van, azaz a kapcsolat egy egyenessel leírható. Na most, ha még emlékeztek elemi iskolai tanulmányaitokból, egy egyenes egyenlete a következő módon írható le:

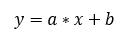
Ha x és y értékét egy grafikonon ábrázoljuk, akkor x értékei lesznek a vízszintes és y értékei a függőleges tengelyen. y értékeit úgy kapjuk meg, hogy x értékeit behelyettesítjük az adott függvény képletébe. Ezután y értékeit ábrázolni lehet a grafikonon x függvényében. Például, ha az y = x függvényt ábrázoljuk, akkor a következő grafikont kapjuk:

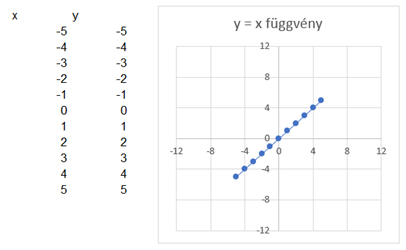Akkor most nézzük meg, hogy néz ki az y = 2*x függvény:

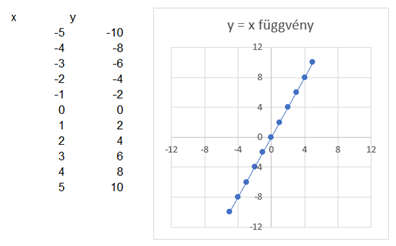
És az y = 0,5*x:

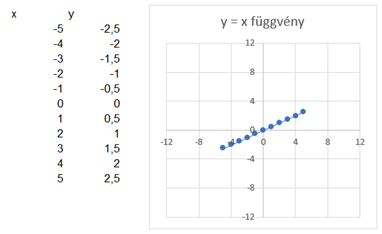
Azaz, ha x-et megszorzom egy 1-től különböző számmal, az az egyenes meredekségét fogja megváltoztatni.

És mi történik akkor, ha az a*x szorzathoz hozzáadok, vagy elveszek belőle egy másik számot? Az y = 1*x+5 függvény így néz ki:

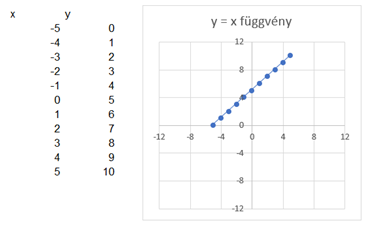
Az y = 1*x-5 pedig így:

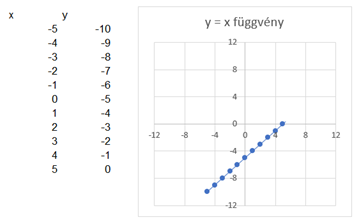
Vagyis amikor 'a*x' értékéhez hozzáadok vagy kivonok egy számot, az eltolja az egyenest felfelé vagy lefelé az y-tengely mentén (vagy jobbra és balra az x-tengely mentén, ahogy tetszik).

Amikor az x és y értékeket ábrázoló pontsorozat alapján akarunk meghatározni egy olyan egyenest, amely szépen rásimul a pontokra, akkor tulajdonképpen az az első és legfontosabb feladatunk, hogy meghatározzuk a és b értékét, azaz egy elméleti függvényt, amely a lehető legjobban leírja az x és az y változó kapcsolatát.

Persze az élet nem ilyen egyszerű, hiszen amikor visszafelé járunk el, azaz a pontok halmaza alapján kell egy elméleti egyenest felállítanunk, akkor szembesülünk a kőkemény és rideg valósággal, hogy a pontok fegyelmezetlen módon nem hajlandók ráfeküdni az egyenesre, hanem kisebb-nagyobb eltéréssel körülötte terülnek el. Vagyis a pontoknak van valamekkora szóródása az elméleti egyenes körül. Attól tartok, hogy az egyenesünk sohasem fogja teljesen tökéletesen leírni a valóságot, mindig csak közelíteni fog hozzá és a függvényünk által megadott pontok sem fogják soha teljesen tökéletesen megjósolni x és y értékeit, csak közelíteni fogják azokat. De erről majd még később.

Az első kihívás az lesz, hogy amikor a pontjaink nem eléggé fegyelmezettek, akkor tulajdonképpen igen sokféle egyenest rájuk tudnánk fektetni és a legtöbbjük akár még jellemezheti is a változók kapcsolatát, de vajon ezek közül melyik az, amelyik legjobban jellemzi ezt a kapcsolatot? Ehhez praktikusan elő kell vennünk egy korábbi leckét (Adathalmazok elemeinek szóródása - A szórás és a variancia), hiszen a fegyelmezetlenül viselkedő pontjaink, amelyek nem hajlandók ráfeküdni az elméleti egyenesre, szóródást okoznak! Nyilván az az érdekünk, hogy ez a szóródás minél kisebb legyen, tehát azt az egyenest kell kiválasztanunk, amelytől a pontok átlagos távolsága a legkisebb. Már korábban elmélkedtem arról, hogy ha a pontok szóródására a pontoknak az átlagtól való távolságát a négyzetre emeljük, az hangsúlyosabbá teszi az átlagtól távolabb lévő pontok eltérését, mert a négyzetre emeléssel ez a távolság exponenciálisan nő (Variancia négyzetgyöke vs. eltérések abszolút értéke).

Mivel az a célunk, hogy a függvényünkkel 'x' értéke alapján megbecsüljük 'y' értékét, ezért a hiba y-irányú összetevője lesz fontos a számunkra, azaz, ha van egy egyenesünk, az az érdekünk, hogy a pontok y-irányú összetevője legyen minimális!

És itt sajnos meg kell szegnem a saját magam számára hozott szabályaimat és el kell adnom a lelkemet az ördögnek, mert muszáj bevezetnem egy újfajta jelölést, ez az ŷ (y-kalap vagy angolul y-hat – ejtsd „y-het”). A későbbiekben az y̅-ra szükségünk lesz, ezért az elméleti függvényünk adott x pontjához tartozó y-értéket fogjuk ezzel jelölni. Sajnos ezt nem lehet megúszni, mert a pontokhoz tartozó különböző y-értékek összekeverhetők lennének, ha nem adnánk az egyiknek egy külön betűjelet.

Az y-irányú összetevőket vizsgálva a történetnek 3 fontos szereplője van minden egyes pont esetében:

• A ponthalmaz i-dik pontja (yi)
• A ponthalmaz i-dik pontjához tartozó becsült érték az Y = ax + b egyenlet alapján (ŷi)
• A ponthalmaz pontjaihoz tartozó y-irányú összetevők átlaga (y̅)

Ezeknek a fontos pontoknak a távolságai szintén fontosak lesznek nekünk:

A teljes távolság (Total) a pont y-irányú távolsága a ponthalmaz összes pontjának y-irányú átlagától. Ez a távolság segít majd meghatározni a pontok teljes varianciáját.

A Maradék hiba (Residual error) adja meg azt, hogy az egyes pontok mennyire térnek el az elméleti egyenestől. Alapvetően annál jobb, minél kisebbek ezek a távolságok, hiszen annál megbízhatóbb lesz az egyenes egyenlete által adott becslés.

A Regresszió / Megmagyarázott (Regression / Explained) távolság a regressziós egyenes és a pontok y-irányú átlagainak a távolsága. Amíg a Total távolság azt adja meg, hogy a ponthalmaz pontjai a VALÓSÁGBAN mennyire szóródnak az átlag körül, addig a Regresszió / Megmagyarázott távolság azt adja meg, hogy a regressziós egyenes által ELMÉLETBEN meghatározott pontoknak mekkora a szóródása.

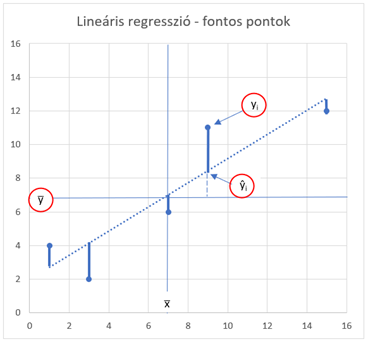
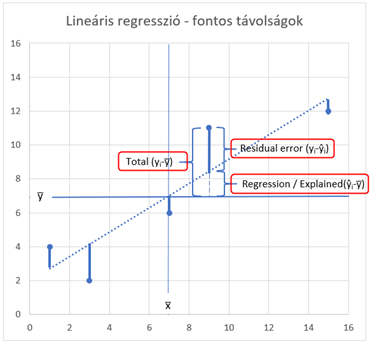
A fenti ábrán látható, hogy az egyes pontokhoz tartozó ilyen távolságokat kell minimalizálnunk, de leginkább a Maradék távolságot. Ezt a távolságok négyzetre emelésével tudom még érzékenyebbé tenni és ha szemléletesebben akarom ábrázolni ezt, akkor minden egyes ponthoz egy akkora négyzetet rajzolok, amekkora a pont y-irányú távolsága az elméleti egyenes y pontjától. Remélem, így érthető lesz.

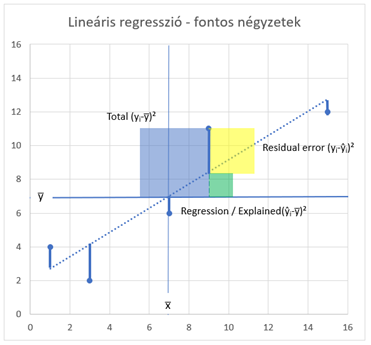
Ha például a teljes távolsághoz (Total) tartozó négyzeteket az összes ponthoz odarajzoljuk és összeadjuk a négyzetek területét, akkor megkapjuk az úgynevezett „Sum of Squares” értéket, amelyet az „SS” rövidítéssel szoktak jelölni. Amikor a Total távolságokat összegezzük, akkor ezt a TSS vagy az SSTotal rövidítéssel szokták jelölni.

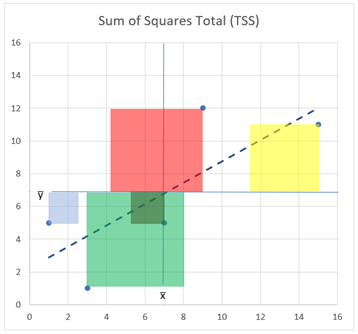
Ugyanezt megtehetjük a Maradék hiba (Residual error), illetve a Regresszió / Megmagyarázott (Regression / Explained) távolságokkal is, amelyeket RSS (SSResidual), illetve az ESS (SSExplained) rövidítésekkel jelölnek:

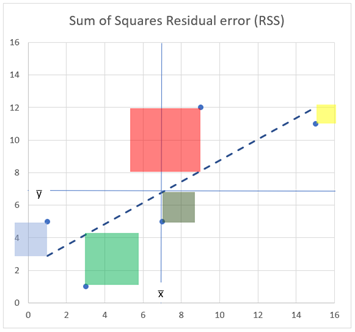
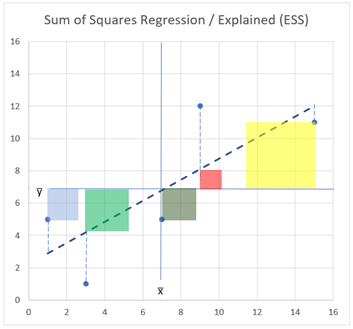
Azért kell ennyiféle elnevezéssel megismerkednünk, mert ahány szakirodalom, annyiféle névvel illetik ugyanazt a dolgot. Ezek a kifejezések a későbbiekben még elő fognak kerülni.

Azt a folyamatot, amikor azt az egyenest keressük, amelynek során a pontok és a függvény által becsült egyenes közé rajzolt négyzetek átlagos területét akarjuk minimálisra csökkenteni, legkisebb négyzetek módszerének (Least Squares method) nevezzük. Hogyan is számoljuk ki a négyzetek területét?

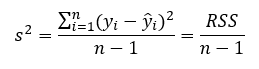
Ez az S² ismerős valahonnan. Igen, ez a variancia vagy szórásnégyzet definíciója, tehát a pontok négyzetes távolsága az átlagtól, vagyis a mi esetünkben az elméleti egyenestől.

Ebben a fejezetben csak az a célom, hogy elhidd, van olyan egyenes, amelynél ez a variancia minimális. Ezt egy példán keresztül szeretném bemutatni. Vegyük a következő egyszerű adatsort:

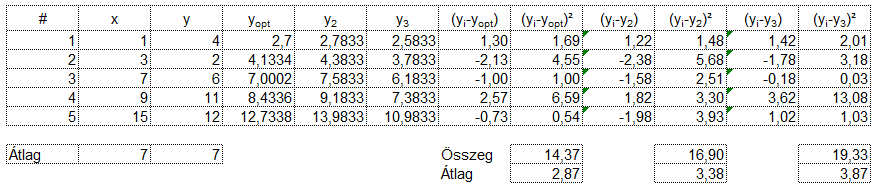
Az adatsorom 5 darab 'x' és a hozzájuk tartozó 5 darab 'y' értékből áll. Az 'yopt' oszlopban kiszámítottam az 'x' értékekhez tartozó optimális függvény alapján kiszámított értékeket. Majd készítettem két olyan függvényt, amelyek felfelé és lefelé eltérnek az optimális függvénytől, és ugyanúgy kiszámítottam az 'x' értékekhez tartozó 'y2' és 'y3' értékeket. Ezután kiszámítottam a három függvényhez tartozó varianciák, azaz a pontokhoz tartozó négyzetek területeit és ezek összegét A táblázat ebben a formában nem kedvez a szemnek, ezért ezeket grafikusan is ábrázoltam:

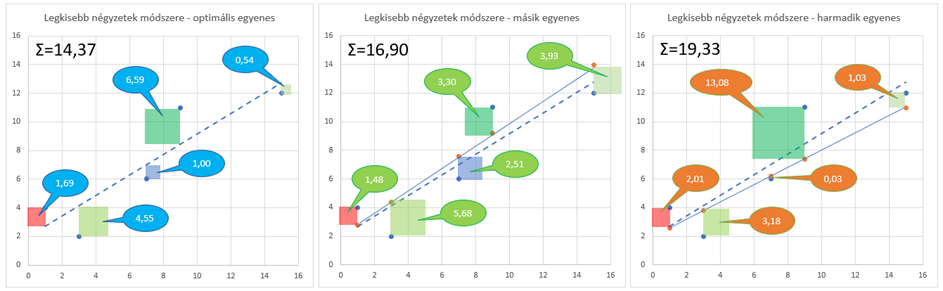
A három grafikonon jól láthatók az egyes pontokhoz tartozó négyzetek területeinek változása az elméleti egyenes megváltozásával. És tényleg, bármelyik irányba térek el az elméletileg legjobb egyenestől, a négyzetek területeinek összege nőni fog!

Ennek a cikknek ennyi volt a célja. Ha megértetted belőle a legkisebb négyzetek módszerének lényegét, az egyelőre elég. A következő bejegyzésben be fogom mutatni azt, hogy hogyan határozható meg ez a bizonyos optimális függvény egyenes, majd a későbbiekben az is, hogy hogyan tudjuk értékelni ennek az egyenesnek a megbízhatóságát, azaz, hogy mennyire pontosan képes megbecsülni 'y' értékét 'x' értéke alapján. Mert ez azért nem olyan biztos...!