Ezzel a témával is foglalkoztam már (Kancsal tengerész nem tud célozni! – Kieső értékek vizsgálata), de ugye itt most az a távlati cél, hogy a Six Sigma módszertanban alkalmazott leggyakoribb eszközöket hogyan tudjuk használni R-ben. Ezt most be is fogom mutatni, de azért lesznek újdonságok is a korábbiakhoz képest.
Először is az utóbbi időben felvett szokásom szerint létrehoztam egy mintát, ez esetben azzal a kitétellel, hogy az adatsornak tartalmaznia kell kieső értékeket is. Ezt úgy értem el, hogy nem egy, hanem két mintát hoztam létre véletlen számokból. Egy 15 eleműt (minta1) és egy 3 eleműt (minta2), majd ezeket összekombináltam és megkevertem.
#A kieső értékeket tartalmazó minta előállítása
minta1 <- rnorm(15, mean = 0, sd = 1)
minta1
minta2 <- rnorm(3, mean = 10, sd = 0.2)
minta2
#A két minta kombinálása egy vektorba
minta <- c(minta1, minta2)
minta
#A mintaelemek sorrendjének megkeverése
minta <- sample(minta)
minta
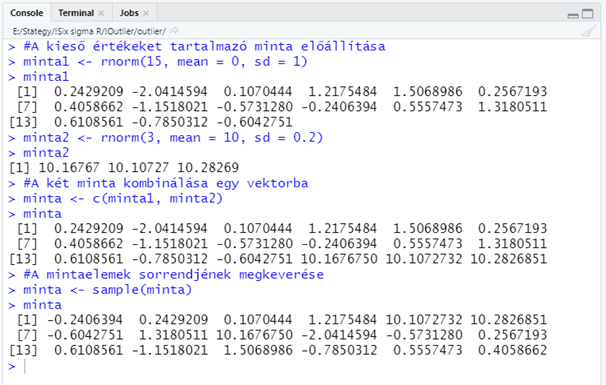
Így egy olyan 18 elemből álló mintát kaptam, amelynek nyilvánvalóan van 3 kieső eleme, ahogyan az a következő diagramból is kitűnik.
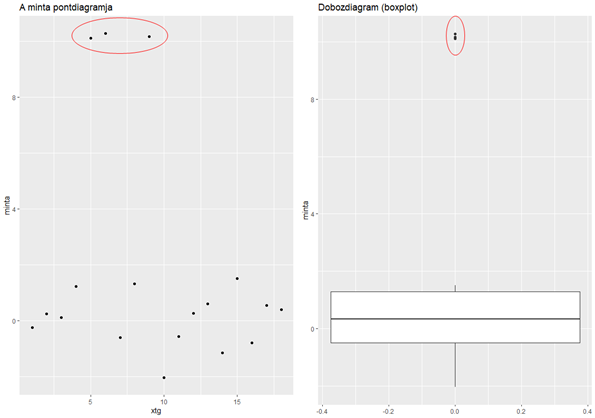
A diagramok elkészítésekor nem alkalmaztam a korábbiakhoz képest nagyon új dolgokat, de egy-két apróságot érdemes megemlíteni.
#ggplot2 és gridExtra csomagok betöltése
library(ggplot2)
library(gridExtra)
#pontdiagram
xtg <- c(seq(1, 18, 1)) #x-tengely beosztása
plot1 <- ggplot() +
geom_point(aes(x = xtg, y = minta)) +
labs(title = "A minta pontdiagramja")
#A minta dobozdiagramja
plot2 <- ggplot() +
geom_boxplot(aes(y = minta)) +
labs(title = "Dobozdiagram (boxplot)")
#A két diagram elhelyezése egymás mellett
grid.arrange(plot1, plot2, ncol = 2)
A pont diagram esetében a pontokat sorrendben szerettem volna ábrázolni. Sajnos a ‘geom_point()’ függvény “igényli” a független változó jelenlétét, ezért létre kellett hoznom egy ‘xtg’ nevű változót, amely 1 és 18 közötti egész számokat tartalmaz szépen sorban. A ‘c()’ és a ‘seq()’ függvények működését már korábban ismertettem (Mi is az a hipotézis vizsgálat?). Ezután már csak a két diagramot kellett elkészítenem. A pontdiagramot a ‘geom_point()’, a dobozdiagramot pedig a ‘geom_boxplot()’ függvény alkalmazásával tudtam elkészíteni. Ezek esetében az x és az y értékeit az ‘aes()’ függvénnyel tudtam megadni, mert ezek meglepő módon esztétikai jellemzőkként vannak kezelve a ggplot2-ben. A többi tulajdonképpen ugyanaz, mint korábban.
A jobb oldali dobozdiagram szépen kiemeli a kieső értékeket. Azt, hogy ezt mi alapján teszi, a cikk elején hivatkozott előző bejegyzésben már elmagyaráztam. Viszont az R megadja a lehetőséget arra is, hogy pontosan megtudjuk, melyik értékek a kiesők. A ‘geom_boxplot()’ diagramhoz hozzátartozik egy több különböző elemből álló kis “adatbázis” is, amelynek az értékeit egy függvény segítségével praktikusan le is tudjuk kérdezni.
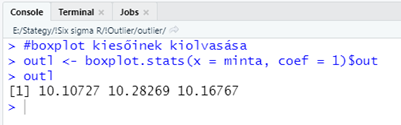
#boxplot kiesőinek kiolvasása
outl <- boxplot.stats(x = minta, coef = 1)$out
outl
A fontos, az az, hogy a ‘boxplot.stats()’ függvény kimenete ez a kis adattábla, amelynek az egyes mezőire ugyanúgy tudunk hivatkozni, mint egy bármilyen más adattáblára, vagyis az oszlop vagy mező nevét a ‘$’ jel után írva. Ekkor a függvény kiírja azokat az értékeket, amelyeket kiesőkként kezel.
Amennyiben az adatsorunk valamilyen paraméteres eloszlást követ, vagyis rá tudunk húzni egy bizonyos paraméterekkel meghívott sűrűségfüggvényt az adatainkra, akkor megpróbálhatjuk a quantilis módszert, azaz a sűrűségfüggvény alapján kiszámoljuk a 95%-os megbízhatósági tartományt és megnézzük, hogy az adatsor mely értékei kerültek ezen kívül. Ennek a módszernek én abban látom a hátrányát, hogy ha kieső értékek vannak egy adatsorban, akkor eleve nehézségekbe fog ütközni, hogy egy paraméteres sűrűségfüggvényt ráillesszünk az adatokra. Ha netán véletlenül ez mégis sikerülne, akkor viszont miért mutatná ki a quantilis módszer a kieső értékeket? Szóval szerintem ez nem igazán működik.
Szokták még alkalmazni az úgynevezett Hampel-szűrőt, amely a mediánt alkalmazza az átlag helyett, így kiküszöböli az átlag kieső értékek általi torzulását. A módszer egyáltalán nem bonyolult.
- Először is kiszámítjuk az adatsor mediánját - Me,
- majd kiszámoljuk az adatsor összes pontjának mediántól mért abszolút távolságát - |Pi – Me|,
- megkeressük az előző pontban kiszámolt távolságok mediánját - Mei,
- végül kiválasztjuk azokat a pontokat, amelyek távolsága nagyobb, mint (4,5*Mei) az adatsor mediánjától (Me)
A |Pi – Me|, azaz az adathalmaz pontjainak abszolút távolsága a mediántól az úgynevezett MAD (Median Absolute Deviation), amely nem egyezik meg a már korábban említett másik MAD-del, amely a Mean Absolute Deviation rövidítése (Variancia négyzetgyöke vs. eltérések abszolút értéke). De honnan jön a 4,5? Miért pont 4,5-tel kell megszorozni a minták távolságainak mediánját ahhoz, hogy megkapjuk a kieső értékek határát? A válasz egy becslés, mely szerint egy adatsor szórása megegyezik a MAD körülbelül másfélszeresével.
![]()
A medián alkalmazása arra utal, hogy ez egy nemparaméteres módszer, azaz az eredmény nem függ az adathalmaz eloszlásától.
R-ben ezt egyrészt egyszerűen ki lehet számítani a következő kód segítségével, illetve a ‘pracma’ nevű csomag tartalmaz egy ‘hampel()’ függvényt, de ezt elsősorban idősorok elemzésekor tudjuk alkalmazni, ott ezt a szűrőt előszeretettel alkalmazzák. Egy ilyen egyszerűbb esetben viszont nem biztos, hogy működni fog a bemenő adatok formátumának eltérései miatt. De nézzük a kódot:
#Kieső értékek meghatározása Hampel-szűrő segítségével
#A minta mediánjának kiszámítása
mintaMedian <- median(minta)
#A minta elemeinek távolsága a minta mediánjától (ebből egy vektor lesz!)
mintaTav <- abs(minta - mintaMedian)
#A mintatávolságok mediánja
mintaTavMedian <- median(mintaTav)
#A kieső értékek kiválasztása (mintaTav > 4,5 * mintaTavMedian)
Kiesok <- minta[mintaTav > 4.5 * mintaTavMedian]
Ebben a kódban az tetszik a legjobban, hogy milyen egyszerűen kiszűrhetők a kieső értékek a mintából. Ezt az teszi lehetővé, hogy noha a minták mediántól mért távolságának adatai teljesen függetlenek a minta adataitól (nincs semmilyen azonosító, ami összekötné őket), de mivel nem változtattam meg ezek sorrendjét, ezért biztosra vehetem, hogy a minták és ezek távolságai a mediántól megfelelő sorrendben vannak.
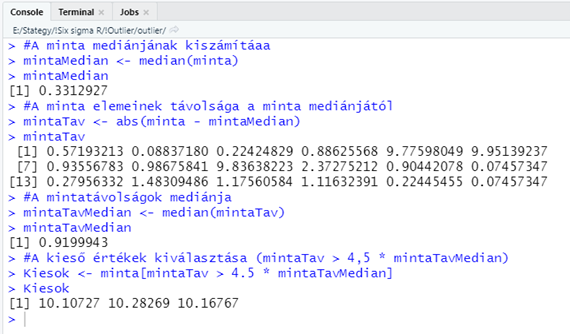
Az eredményként kapott három adat tökéletesen megfelel a dobozdiagram által már kimutatott kieső értékeknek.
A cikk elején hivatkozott előző bejegyzésemben már említettem, hogy léteznek hipotézis vizsgálatok is a kieső értékek vizsgálatára, mint amilyen a Grubb’s teszt vagy a Dixon’s teszt. Ezek elterjedten alkalmazott tesztek, így természetesen az R-ben is megtalálhatók. A kieső értékek detektálására létezik egy külön csomag az ‘outliers’. Ebben találhatók a ‘grubbs.test()’ és a dixon.test()’ függvények, amelyekkel a fent említett teszteket el tudjuk végezni. Ezek részletes leírását és használatának módját a cikk elején hivatkozott bejegyzésben megtalálod.
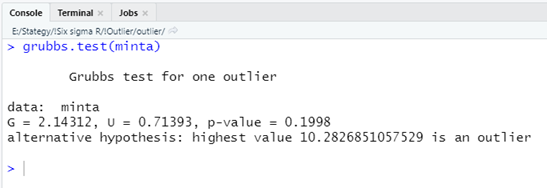
Érdekes módon a Grubb’s teszt eredménye az lett, hogy a minta adatsorban NINCSENEK kieső értékek! A p-érték 0,1998, ami nagyobb, mint 0,05, vagyis a nullhipotézist el kell fogadnunk! Erre minimum annyit mondanék meghökkenve, hogy “nocsak”, hiszen fentebb ugyanebben az adatsorban hármat is találtam a korábban említett módszerekkel! Sajnos a szakirodalom is megerősíti, hogy mind a Grubb’s teszt, mind pedig a Dixon’s teszt eléggé konzervatív a kieső értékek kijelzésében.
És akkor most jön a legjobb rész!
A tesztet úgy hívják, hogy “általánosított extrém studentált eltérő érték” teszt (generalized Extreme Studentized Deviate test, vagy generalized ESD test), de profán módon csak úgy egyszerűen Rosner-tesztnek is nevezik. Ezt a tesztet még nem ismertem, de mind közül ez lett a kedvencem. Egyrészt, mert végre egy outlier teszt, ami nemcsak egy kieső értéket képes detektálni, hanem akár az összeset is, másrészt mert az algoritmusa nagyon egyszerű és ötletes, harmadrészt pedig mert a megvalósítása R-ben nagyon egyszerű és kényelmes. A korábban említett Grubb’s és Dixon’s tesztek esetében a nullhipotézis az volt, hogy az adathalmazban nincs kieső érték, az ellenhipotézis pedig az, hogy az adatsorban legalább egy kieső érték van. A Rosner-teszt esetében a nullhipotézis és az ellenhipotézis a következő.
- Ho: A vizsgált ‘n’ elemű adathalmazban nincsenek kieső értékek
- H1: A vizsgált ‘n’ elemű adathalmazban ‘r’ darab kieső érték van.
A módszer ravaszsága abban van, hogy ez egy iteratív módszer, amelynek külön pikantériája, hogy nem kell pontosan tudnunk előre a kieső értékek számát. Ha körülbelül sejtjük, hogy hány kieső érték lehet a vizsgált adatsorban, akkor elég egy ennél nagyobb számot megadni a teszt megkezdésekor. Ez azt jelenti, hogy mondjuk az általam vizsgálat adatsorban azt sejtem, hogy 3 kieső érték lehet (ez lesz ‘r’), akkor a teszt megkezdésekor megadom, hogy szerintem a kieső értékek száma 4 vagy 5, esetleg 6 (ez lesz a ‘k’). A teszt végrehajtása után az eredmény meg fogja mutatni, hogy pontosan hány kieső érték van az adatsorban. Azt viszont legalább sejtenünk kell, hogy a kieső értékek kisebbek vagy nagyobbak, mint az adatsor többi része.
- A teszt végrehajtásakor először is nagyság szerint sorba rendezzük a vizsgált adatsor elemeit. A kiválasztott ‘k’ darab értékre kiszámítjuk az
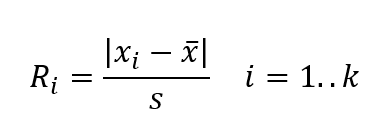
próbastatisztikát, ahol x̅ a vizsgált adathalmaz átlaga, s pedig a szórása.
- Ezután az ‘k’ adat közül eltávolítjuk azt az adatot, amelynél Ri értéke a legnagyobb, majd újraszámoljuk az adatsor átlagát és szórását az előbb eltávolított elem nélkül.
- Ezután újra kiszámoljuk Ri értékeit a fenti képlet segítségével, most már k-1 értékre.
- Ezután újra eltávolítjuk azt az elemet, amelynél az Ri értéke a legnagyobb, és így tovább mindaddig, amíg i értéke 1 nem lesz. Természetesen minden körben eltároljuk Ri maximális értékeit.
- Ezután jön a próba határértékének kiszámítása, amely egy fokkal bonyolultabb képlet segítségével történik.
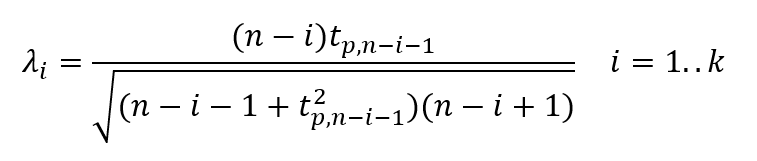
A ‘tp,ν’ értéke a df = ν szabadsági fokú student-féle t-eloszlás (A sörfőző, aki forradalmasította a statisztikát) p valószínűségéhez tartozó érték, ahol

ahol α 95%-os megbízhatósági szint esetén 0,05, 99%-os esetén 0,01, és így tovább.
A lényeg, hogy a mintában annyi kieső érték van, amelyik ‘i’ esetében az Ri próbastatisztika értéke nagyobb, mint a λi értéke. Természetesen megértem, hogy a fenti leírás nehezen követhető, ezért elkészítettem ezt a példát táblázatkezelőben is a jobb láthatóság kedvéért, ezt a cikk végén le tudod tölteni az R szkriptekkel együtt.
A táblázat bal oldalán látható az eredeti adatsor. Ezt először is nagyság szerint csökkenő sorrendbe rendeztem, majd kiszámítottam az adatsorok átlagait és szórásait. A sorba rendezés miatt mindig a legfelső elem fog kiesni, ezért tudom a szükséges átlagokat és szórásokat ezen a módon kiszámítani.
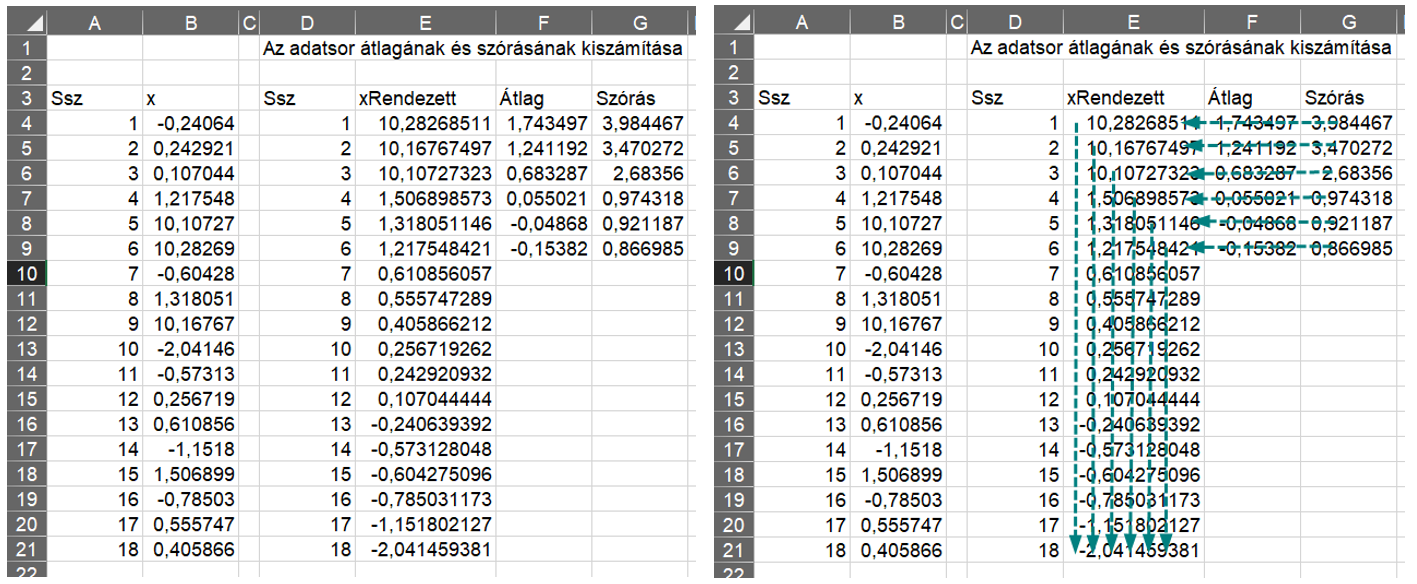
Ezután kiszámítottam az Ri próbastatisztikákat (az első táblázatot addig elrejtettem, hogy látszódjanak a sorok számai). Itt már jól látható, hogy a sorbarendezés miatt mindig a legelső Ri érték a legmagasabb, ezeket meg is vastagítottam. Arra kellett vigyázni, hogy mindig a megfelelő átlagokat és szórásokat használjam.
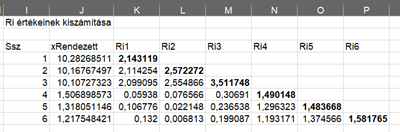
Most jön a feketeleves, a Lambda határértékek kiszámítása.
- Először p értékét számítottam ki a fenti képlet segítségével. Itt mindenképpen kiemelném, hogy α értékének 0,5-öt kell használni, n értéke ez esetben 18, i értékét pedig a Ssz oszlopban lévő szám adja meg.
- Ha p megvan, akkor a ‘t.inverz()’ függvény segítségével ki lehet számolni, hogy milyen x - érték tartozik a nu = n - i – 1 szabadsági fokú student-eloszlás p valószínűségéhez.
- Ezután ezt egyszerűen négyzetre emeltem, mert ez kell majd a Lambda nevezőjébe.
- Ezután jött a számláló és a nevező kiszámítása, majd ezek hányadosa megadja Lambda értékét.
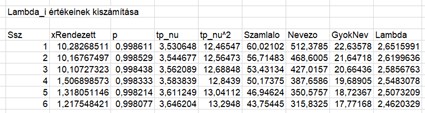
Végül jön a döntés, hogy hány kieső érték van az adatsorban. Ri értéke a harmadik sorban nagyobb, mint a Lambda határérték, így az eredmény az, hogy három kieső érték van az adatsorban.
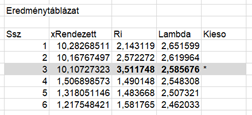
A teszt hátránya az, hogy az adatsornak közelítőleg normál eloszlásúnak kell lennie a próbastatisztika standardizáló képlete miatt, ezért a Rosner-teszt alkalmazása előtt ez esetben érdemes ellenőrizni az adatok normalitását (Ha nem normál eloszlás, akkor micsoda? – adatsor eloszlásának azonosítása R-ben (Six Sigma in R)). Összességében elmondható, hogy a Rosner-teszt tulajdonképpen egymás után végrehajtott Grubb’s-tesztek sorozata egy kicsit fűszerezve, de a képletek bonyolultsága ellenére nem vészes az alkalmazása. Mondjuk azt ne kérdezd meg, hogy miért működik…
Most nézzük meg, hogy néz ez ki R-ben. Az ‘EnvStats’ csomag kezd egyre inkább a kedvencem lenni, mert a ‘rosnerTest()’ függvény is ebben a csomagban van benne. Szerencsére ennek az alkalmazása is egészen egyszerű, összesen négy potenciálisan alkalmazható paramétere van.
x – A vizsgálandó adatsor
k – a valószínű kieső értékek száma, amit én fentebb is k-val jelöltem. Az a fontos, hogy ez nagyobb legyen, mint ahány kieső értéket sejtünk az adatsorban.
alpha – A választott megbízhatósági szint, lehet 0,05 vagy 0,01 vagy akár más is…
warn – Ez egy logikai paraméter, ha TRUE az értéke (ez az alappbeállítás), akkor az eredmény nyomtatásakor a függvény figyelmeztetést ad, ha az elsőfajú hiba (Type I error) túl magas.
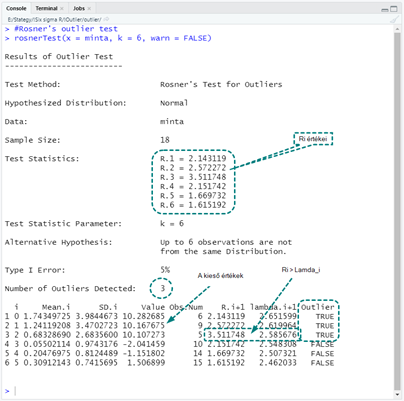
Az eredmény a fenti részletes magyarázatok függvényében jól értelmezhető. Ri értékei láthatók a riport közepén és az alul lévő táblázatban is. A ‘Mean.i’ és az ‘SD.i’ oszlopokban láthatóak a mintaátlagok és a szórások, a ‘Value’ oszlopban a minta értékei, az ‘Obs.Num’ oszlop adja meg, hogy az értékek eredetileg hányadikak voltak az adatsorban. Az ‘R.i+1’ és a ‘lambda.i+1’ oszlopokban vannak az Ri és a Lambda_i értékek, az ‘Outlier’ oszlop pedig a kieső értékek azonosítását tartalmazza IGAZ vagy HAMIS jelöléssel, ahol természetesen a TRUE-val jeölt értékek a kiesők.
Összegzés:
Bár az elején nem számítottam rá, ismét sikerült újat tanulnom. A Hampel-szűrő és a Rosner-teszt is tetszik, jól kiegészítik az eddigi ismereteimet. Az ‘EnvStats’ csomagnak is egyre több hasznos függvényét ismerem meg, úgy látom, még fogunk vele találkozni a jövőben is. Végezetül külön szeretném kiemelni, hogy a kieső értékek azonosítása esetében ezek csak az első lépések, léteznek már olyan gépi tanulási algoritmusok is, amelyek a fentieknél bonyolultabb problémák esetén is alkalmazhatók, mint például a DbScan (Density Based Spatial Clustering of Applications with Noise) vagy az Isolation Forests, de ezekkel majd talán később fogok foglalkozni.
Az excel táblázatot és az R szkripteket innen tudod letölteni.
Források:
Package ‘outliers’
https://cran.r-project.org/web/packages/outliers/outliers.pdf
Manoj K, Senthamarai Kannan K: Comparison of methods for detecting outliers, International Journal of Scientific & Engineering Research, Volume 4, Issue 9, September-2013
What is a “Hampel Filter” and how does it work? - Stackexchange
https://dsp.stackexchange.com/questions/26552/what-is-a-hampel-filter-and-how-does-it-work
Peter J. Rousseeuw: Robust Estimation and Identifíing Outliers,
https://wis.kuleuven.be/stat/robust/papers/publications-1990/rousseeuw-robustestimation-handbookengineersscient.pdf
Engineering Statistics Handbook: Generalized ESD Test for Outliers
https://www.itl.nist.gov/div898/handbook/eda/section3/eda35h3.htm
rosnerTest function - RDocumentation
https://www.rdocumentation.org/packages/EnvStats/versions/2.3.1/topics/rosnerTest





