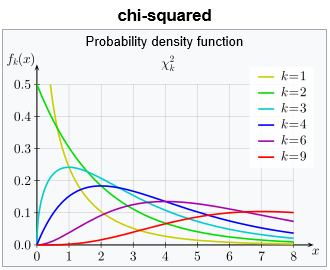
Mielőtt tovább mennénk a különféle statisztikai tesztek dzsungelében, sajnos nem ússzuk meg egy-két további eloszlás típussal (sajnos lesz még egy pár). A következő eloszlás típus, amiről szót kell ejtenünk az úgynevezett Khí-négyzet eloszlás.

Ez egy eléggé titokzatos eloszlás típus, legalábbis egy fokkal bonyolultabb, mint amiket eddig tárgyaltunk. Amint azt majd látni fogjuk, a képet az is össze fogja zavarni, hogy a későbbiekben tárgyalt tesztekben a legkülönfélébb képletekkel kiszámolt értékekről fogjuk azt állítani, hogy Khí-négyzet eloszlást követnek, ami szintén nem segíti a megértést. Ettől függetlenül ugorjunk neki a témának és próbáljuk meg értelmezni, hogy mi is ez az eloszlás.

Az eddig tárgyalt hipotézis vizsgálatok esetében a sokaság és a minta átlagát vizsgáltuk, de nem sok szót ejtettünk a sokaság vagy a minta szóródásáról. De vajon hogyan értelmezzük egy normál eloszlású sokaság vagy minta szóródását? A képzett olvasó rögtön rávágja, hogy a varianciával és a szórással (Adathalmazok elemeinek szóródása - A szórás és a variancia). Idézzük fel, mi is egy sokaság varianciájának képlete:

És mi történik akkor, ha a fenti variancia képletét a standard normál eloszlásra alkalmazom, amelynek az átlaga 0 és a szórása 1? Az egyszerűség kedvéért vegyünk 1 darab tetszőleges mintát a standard normál eloszlásból és számoljuk ki ennek a mintának az átlagtól való eltérését a fenti képlet alkalmazásával. A minta jele legyen Z. Ha behelyettesítjük az átlag helyére a 0-t és a mintaszám helyére az 1-et, akkor a következőt kapjuk:

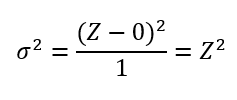
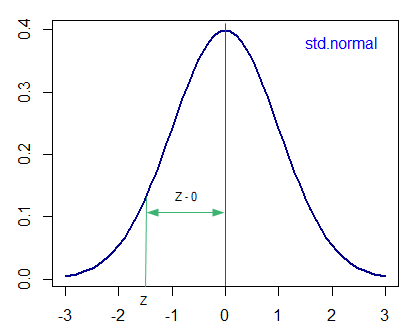
Mit is jelent ez grafikusan? Az alábbi képen látható a standard normál eloszlás képe. Amint azt már többször tisztáztuk, Z értéke a diagram x-tengelyén lévő mennyiség, Z távolsága pedig Z-nek az x-tengellyel párhuzamos távolsága az átlagtól, azaz jelen esetben 0-tól.

Ha még emlékeztek a Bernoulli eloszlás magyarázatára, ott is hasonló volt a helyzet (A Bernoulli-eloszlás a gyakorlatban, avagy a vizuális ellenőrzés pszichológiája). A Bernoulli eloszlás esetében volt egyetlenegy olyan eseményünk, amelynek csak két végkimenetele volt lehetséges, majd ezt a kísérletet megismételtük n alkalommal, így kaptunk n darab egymástól független eredményt. Most csináljunk itt is valami hasonlót, ismételjük meg a fenti folyamatot n-szer, tehát vegyünk ki a standard normál eloszlásból n-szer 1 darab egymástól független mintát, ábrázoljuk ezeknek a mintáknak a négyzeteit egy a standard normál eloszláséhoz hasonló sűrűségfüggvényen (amely megmutatja, hogy adott Z-négyzet hányszor fordult elő az n darab minta között), majd ez alapján vizsgáljuk meg ennek az n elemű adathalmaznak az eloszlását.

Íme:

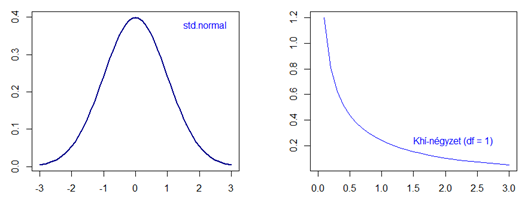
Talán nem árulok el titkot, az eredmény nem normál eloszlású lesz, hanem egy teljesen más eloszlást fog mutatni. Ezt hívjuk Khí-négyzet eloszlásnak, ha a szabadsági fokok száma (df) 1. Az eredmény látható a fenti diagramokon, amiken máris meg lehet figyelni néhány dolgot. Egyrészt ez a Khí-négyzet eloszlás szemmel láthatóan egyoldali eloszlás és csak pozitív értékeket vehet fel. Ez nem is meglepő, figyelembe véve azt, hogy a negatív számok négyzete is pozitív. Igazából az sem teljesen meglepő, hogy a 0 közelében nagyon sok érték található, hiszen a standard normál eloszlás esetében -1 és +1 között van az elemek majdnem 70%-a. És persze azt is tudjuk, hogy ha egy egynél kisebb számot a négyzetre emelünk, akkor annak az értéke még inkább csökken, tehát minél közelebb van Z értéke 0-hoz, még annál is közelebb lesz annak a négyzete. Ebből az következik, hogy a nullához közelebbi értékek gyakorisága igencsak megnő a standard normál eloszláséhoz képest is.

De göngyölítsük tovább ezt a folyamatot, most vegyünk ki KETTŐ darab véletlenszerű mintát a standard normál eloszlású sokaságunkból, nevezzük el őket Z1-nek és Z2-nek, majd nézzük meg a két minta szórását.

Vizuálisan megjelenítve ez így néz ki. És hogyan néz ki az, ha az első esethez hasonlóan ábrázoljuk a két minta négyzetének összegét?

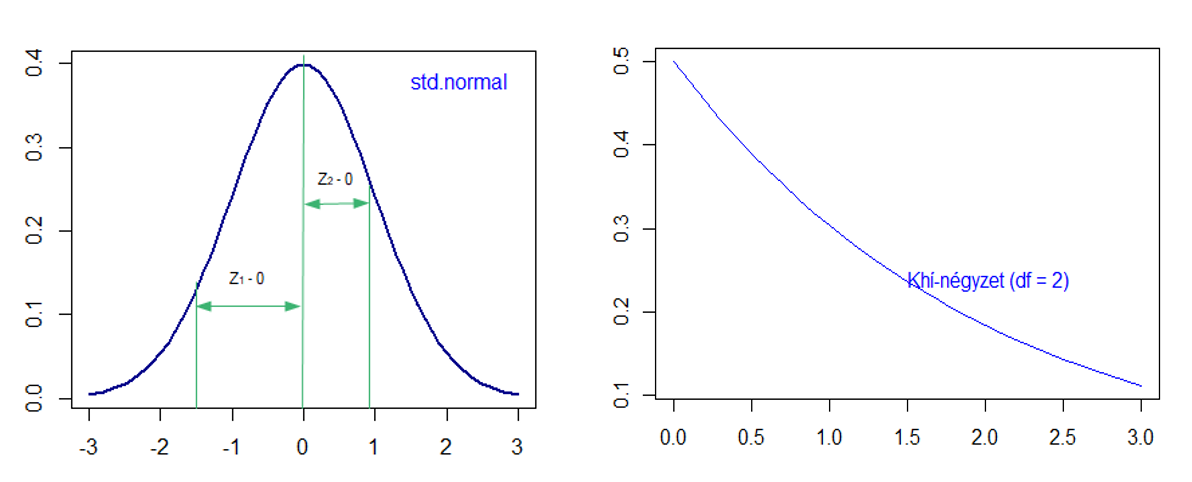
Összehasonlítva a jobboldali grafikont az előző khí-négyzet grafikonnal, akkor az ötlik először a szemembe, hogy itt már sokkal „egyenesebb” a görbe, mint df = 1-nél, azaz még itt is sok a nullához közeli érték, de már több az olyan is, ami nullához még közel van, de már nagyobb. Ennek számomra csak egy logikus oka lehet, hogy ha két értéket választok ki véletlenszerűen, akkor megnő annak a valószínűsége, hogy a kettő közül legalább az egyik egy nagyobb érték és jelentősen lecsökken annak az esélye, hogy a két szám összegének egy nullához nagyon közeli szám lesz az eredménye.

Most növeljük meg a független minták számát még eggyel. Így a képlet a következő lesz:

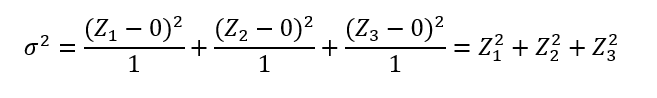
A diagram pedig a következő:

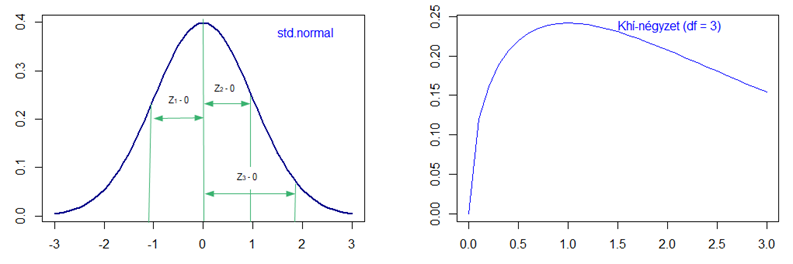
Oh, itt teljesen megváltozott a görbe képe. A három független minta esetében már radikálisan lecsökkent annak a lehetősége, hogy a három független minta összege egy nullához nagyon közeli érték legyen, most már az 1 körüli értékekből van a legtöbb és csak ezután kezdenek el csökkenni az ennél nagyobb értékek gyakoriságai. Ennek gondolom az lehet az oka, hogy annak már tényleg nagyon kicsi a valószínűsége, hogy mindhárom minta értéke annyira kicsi legyen, hogy az összegük is egészen közel legyen 0-hoz.  

Egy kicsit lerövidítve a gondolatmenetet, nézzük meg, hogy hogyan változik a khí-négyzet függvény alakja, ha a minták számát egyesével tovább növeljük.

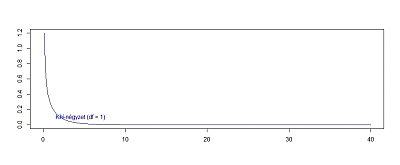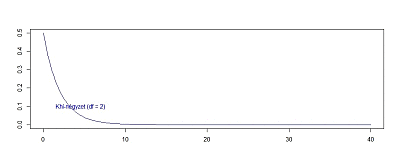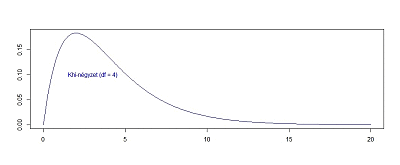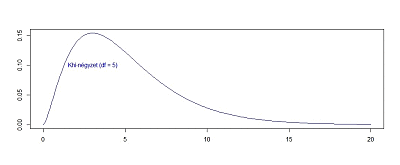Még egy kicsit felgyorsítva a folyamatot lássuk, hogy hogyan változik a függvény alakja akkor, ha a minták számát fokozatosan 60 darabig emelem:

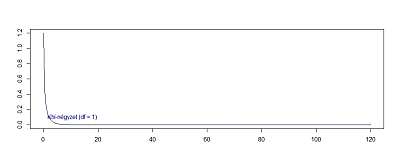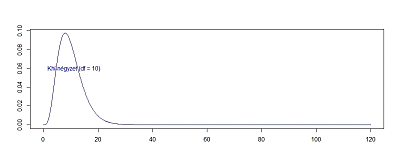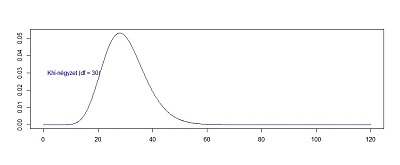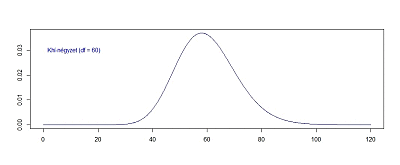 60 darab minta esetében a khí-négyzet függvény alakja már szemmel láthatóan jól közelíti a normál eloszlás függvény alakját, bár még nem tökéletesen, vagyis a 60 darab független minta négyzetének összege már közel normál eloszlást követ. Addig viszont nem, ezért van szükségünk a khí-négyzet eloszlásra, hogy kisebb elemszámú minták esetében is tudjuk becsülni a minták szórását.

Ennek a bejegyzésnek csak annyi volt a célja, hogy bemutassa a khí-négyzet eloszlást, mert a későbbiekben majd látni fogjuk, hogy ez az eloszlástípus sok helyen hasznos lesz nekünk. A konkrét alkalmazási területeket majd további cikkekben fogom részletesen ismertetni.