Korábbi írásaimban (A sörfőző, aki forradalmasította a statisztikát, illetve Z helyett t – leheletnyi különbség) bemutattam az egymintás t-próbát, amelyről kiderült, hogy sem unalmas, sem pedig bonyolult téma. Van azonban a tesztnek egy kicsi szépséghibája, mégpedig az, hogy a t-próba érzékeny a vizsgált minta eloszlására. A Student-féle egymintás t-próba azt feltételezi, hogy a minta eloszlása szimmetrikus.  Ha a minta valójában aszimmetrikus, azaz valamelyik irányba „dől”, akkor az eloszlás egyik szélsőértékénél az elsőfajú, a másik végénél viszont a másodfajú hiba elkövetésének valószínűsége fog megnőni, azaz nagyobb valószínűséggel fogunk téves döntést hozni.

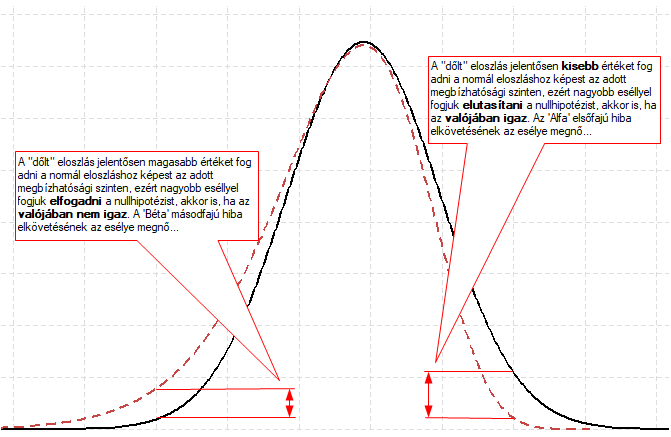
Egy Johnson nevű úriember - akiről a próbát elnevezték - azt a ravaszságot találta ki, hogy a dőlés függvényében korrigálni kell a ’t’ próbastatisztika értékét. Igen, de milyen irányban és mennyivel?

Az biztos, hogy ez a korrekciós tényező függ a minta átlagától és szórásától, hiszen a normál eloszlást elsősorban ez a két paraméter határozza meg. Függ a mintában lévő értékek darabszámától is valamilyen módon, mert a centrális határeloszlás alapján a sokaságból kivett minták átlagának szórása függ a minta elemszámától, hiszen minél több elemű a minta, a mintaátlag annál jobban közelít a sokaság átlagához. És természetesen ez a korrekciós tényező valahogyan függeni fog a „dőlt” minta dőlésének mértékétől, amelyet ugye a mintaeloszlás ferdeségével jellemzünk. Az úriember által kitalált képlet így néz ki:

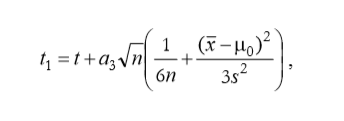
ahol

• a3 a minta ferdeségi együtthatója,
• n a minta elemszáma,
• x̅ a minta átlaga,
• µ0 a sokaság feltételezett átlaga,
• s2 pedig a minta szórásnégyzete (varianciája).

A képlet keletkezését számomra a nemtudás üdvözítő homálya fedi, de az jól látható, hogy körülbelül azok a tényezők vannak benne, amelyeket fentebb felsoroltam. Annyi a lényeg, hogy a Johnson-próba elvégzéséhez előbb ki kell számolni a ’t’ próbastatisztikát a Student-féle egymintás t-próba segítségével, majd a kapott ’t’ értékét módosítani kell a fent látható képlet segítségével. Az így kapott módosított próba statisztika alkalmazása innentől ugyanaz, mint a Student-féle teszt esetében. A minta elemszáma alapján ki kell keresni a próba határértékét és ha a kapott t1 próba statisztika értéke kisebb, mint a próba határérték, akkor elfogadom a nullhipotézist, ha pedig nagyobb, akkor elutasítom.

Utolsó kérdésként felvetődik, hogy mikor érdemes ezt a próbát alkalmazni a sima egymintás t-próba helyett. Egy korábbi bejegyzésben (Értékelhető-e egy görbe alakja néhány együttható alapján?) már megemlítettem, hogy a ferdeségi és a lapultsági együtthatók alapján akkor tekinthető egy adathalmaz normál eloszlásúnak, ha a fenti két együttható értékei -0,5 és +0,5 között vannak. Ha ezek -1 és -0,5, illetve 0,5 és 1 között vannak, akkor közepes mértékű alakeltérésről, míg, ha ezek -1-nél kisebbek vagy 1-nél nagyobbak, akkor nagyobb mértékű aszimmetriáról beszélhetünk. Szubjektív véleményem szerint a Johnson-féle t-próba alkalmazására csak komolyabb ferdeségi eltérések esetén van szükség, azaz ha a ferdeségi együttható értéke 1-nél nagyobb vagy -1-nél kisebb, vagyis amikor az együtthatók értékei alapján gyanítjuk, hogy az adatsor nem normál eloszlású.

Noha a Johnson t-teszt alkalmazása nem sokkal bonyolultabb, mint a Student-féle t-teszté, úgy gondolom, hogy mielőtt elmegyünk ebbe az irányba, érdemes az adatok normalitását más - egyébként jól működő - tesztekkel is ellenőrizni, pl. Khí-négyzet próbával (Karl Pearson és a rulettkerék rejtélye – Khí-négyzet próba az illeszkedés vizsgálatára), vagy a Kolmogorov - Smirnov illetve az Anderson-Darling tesztekkel, amelyeket eddig még nem tárgyaltam a blog hasábjain.

Forrás:

• Vargha András: Matematikai Statisztika Pszichológiai, nyelvészeti és biológiai alkalmazásokkal, Pólya kiadó, Budapest 2008
• Vargha András: Robusztussági vizsgálatok az egymintás t.próbával, KSH, 2003
  http://www.ksh.hu/statszemle_archive/2003/2003_10/2003_10_872.pdf