forrás: Wikipédia
A német tank probléma a nevét egy a II. Világháború idején felmerült problémára alkalmazott megoldás után kapta. A szövetséges haderők számára nagyon fontos lett volna ismerni, hogy a németek mennyi Panzer V („Panther” azaz párduc) típusú tankot gyártottak a háború évei alatt. A szövetséges hírszerzés minden erőfeszítés ellenére sem volt képes megbízható számadatokkal szolgálni. Végül rájöttek, hogy a németek nagyon precízen egymás után következő egyedi sorszámokkal látták el a legyártott tankok sebességváltó házait. Ekkor elkezdték összegyűjteni a kilőtt vagy elfogott tankokon található sorszámokat és ezek alapján sikerült megbecsülni a legyártott tankok számát, amely lényegesen kisebb volt, mint a hírszerzési becslések. A háború végén, amikor a Szövetségesek végül hozzájutottak a németek termelési adataihoz, akkor derült ki, hogy a tankok sorszámai alapján kiszámított becslések sokkal pontosabbak voltak, mint a szövetséges hírszerzés által adott információk.
Mivel a számítás nem túl bonyolult és egyébként tanulságos, ezért ezt itt és most megosztom veletek.
A becslés ötlete abból indult ki, hogy minden tankon csak egy egyedi sorszám található és a tankok a sorszámokat a gyártás sorrendjében kapják. Ekkor kijelenthető, hogy minden sorszám kiosztásának valószínűsége azonos. Tegyük fel, hogy öt tank sorszámát kaptuk meg, amelyek a következők:
1, 31, 43, 79, 115
Ezek közül a legnagyobb sorszám a 115, tehát ennyi tankot biztosan legyártottak a németek. De vajon mennyivel többet? A feladat tulajdonképpen az, hogy egy korlátozott számú minta alapján meg kellene becsülni, hogy mekkora a sokaság mennyisége. A becsléshez többféle módszert is kipróbáltak, például egyszerűen vették a sorszámok átlagát és azt szorozták meg kettővel, vagy vették a sorszámok szórásának ötszörösét, de ezek közül egyik sem vált be igazán. Végül egy igen egyszerű módszert találtak a becslésre. Annyit tettek, hogy vették az egyes sorszámok közötti távolságok átlagát és ezt az átlagot adták hozzá a legnagyobb sorszámhoz:
Vegyük az egyes sorszámok közötti távolságokat. Ne felejtsük el, hogy diszkrét és nem folytonos számsorról beszélgetünk! Azért kell mindig két x érték közötti távolságból még 1-et kivonni, hogy ugyanaz a sorszám kétszer ne forduljon elő. Ezek alapján a következő egyenletet kapták:
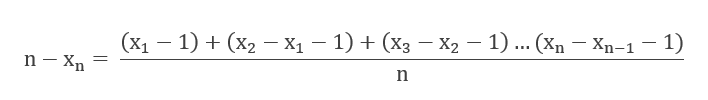
Mivel csak összeadások és kivonások vannak a számlálóban, így a zárójeleket ki lehet törölni, illetve ezután az x1 -x1, x2 -x2, … , xn-1 -xn-1 párokat is ki lehet törölni. Így marad Xn és n-szer -1, azaz n a számlálóban.
Most a számlálóban lévő kivonás mindkét tagját elosztjuk n-nel külön-külön. Mivel n osztva n-nel az egy, ezért megkapjuk a lenti egyenletet.
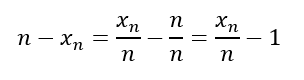
Az egyenletből n-t kifejezve pedig megkapjuk az n-re vonatkozó becslés egyenletét.
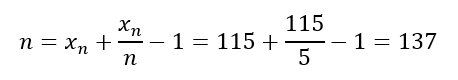
Tehát a németek által legyártott tankok számát úgy becsülhetjük meg, hogy a legnagyobb sorszámhoz hozzáadjuk a legnagyobb sorszám és a minták számának hányadosát és még kivonunk belőle egyet, így a fenti példa adatai alapján a becslésünk az, hogy a németek az adott időszakban 137 tankot gyártottak.
Irodalom:
(Roger W. Johnson, Estimating the size of a population, 1994)
(Richard Ruggles, Henry Brodie: An empirical approach to economic intelligence in World War II)
Mellékesen jegyzem meg, hogy ezt a levezetést ebben a formában sehol sem találtam meg. A fent hivatkozott cikk az egyetlen, ahol megközelítőleg ennyire egyszerűen magyarázza el a szerző a problémát, többségében még az angol nyelvű hivatkozások is egy sokkal bonyolultabb levezetésre hivatkoznak. Ennek ellenére az eredmény ugyanaz..
