
Nem biztos, hogy mindenki így tanulta a kombinatorikát, de amikor először megláttam ezt a fajta levezetést, akkor rögtön beugrott, hogy én ezt így már hallottam valamikor az általános iskolában vagy a gimnáziumban. Én mindig is kevertem a permutációt, a kombinációt és a variációt szóval nem árt, ha tisztázzuk valamilyen egyszerű és játékos módszerrel, hogy melyik mi is valójában.
De először tisztázzuk, hogy mi is az a kombinatorika valójában, mert ez is csak egy idegen kifejezés. A kombinatorika a matematika azon területe, amely azzal foglalkozik, hogy hányféleképpen tudunk dolgokat sorba rendezni, vagy dolgok halmazából hányféle módon tudjuk kiválasztani a halmaz megadott számú elemét.
A kombinatorikával kapcsolatban három fogalom szokott igen gyakran előkerülni, ezek a permutáció, a kombináció és a variáció. Ezeket természetesen hasonló hangzásuk miatt remekül össze lehet keverni és egy idő után természetesen senki sem emlékszik fejből, hogy melyik mire való és mikor használjuk.
Akkor most próbáljuk meg tisztázni, hogy melyik mire való és egyben megpróbálok találni valamilyen egyszerű módszert a három fogalom megjegyzésére is. Felvezetésül jöjjön a klasszikus székfoglalós példa:
Tegyük fel, hogy van előttünk öt darab szék és öt gyerek: Aladár, Beáta, Csaba, Dénes és Eleonóra. Kérdés, hogy hányféleképpen tudjuk leültetni az öt gyereket az öt székre. A tréfamesterek elkedvetlenítése érdekében természetesen nem ér, ha két gyerek egymás ölébe ül, vagy két széket egymásra teszünk. szóval a hasonló trükkös megoldásokat kerüljük, mind az öt gyereknek le kell ülnie valamelyik székre. Tehát lássuk:

- Az első székre bármelyik gyereket le tudom ültetni, hiszen még egyik sem ül, tehát ötféle lehetőségem van a gyerekek közül valamelyiket leültetni. A jobb áttekinthetőség kedvéért a székeket számokkal, a gyerekeket betűkkel jelöltem.

- A második székre már csak négy gyerek közül tudok választani, hiszen az egyik már ül az első széken. Eddig tehát húszféle lehetőségem van, hiszen bármelyik gyereket is ültetem le az első székre, a második székre le tudok ültetni egy másik gyereket a megmaradt négy közül (ha az egymás alatti ábrákat nézed, akkor könnyebben érthető az ábra).
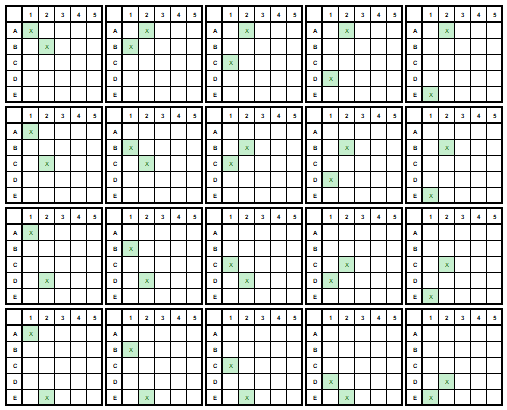
- A harmadik székre már csak három gyerek közül tudok választani, mert az első két székre már leültettem két gyereket. Így tehát már 60-féle lehetőségnél tartunk, hiszen az első székre ötféleképpen, a második székre négyféleképpen, a harmadik székre pedig háromféleképpen tudom leültetni a gyerekeket.
(Ha esetleg van valakinek kedve végigbogarászni…)
- A negyedik székre már csak két gyerek marad, tehát ha az előbb felvázolt összes lehetőség esetén még van két gyerekünk, akit le tudunk ültetni, akkor 2 x 60 = 120 különböző módon tudjuk leültetni a gyerekeket, hiszen az ötödik székre minden esetben egyetlen gyerek fog maradni.
Ha összegezzük a fenti gondolatmenetet, akkor azt kapjuk, hogy az öt gyereket 5 x 4 x 3 x 2 = 120 különböző módon tudjuk leültetni. Bár nem szeretem, hogy be kell vezessek egy új jelölést, mert megfogadtam, hogy ezen blogon nem lesznek mágikus jelek, de most mégis kivételt teszek, mert ez talán még nem bonyolult annyira, hogy ne lehetne megemészteni. Amikor így összeszorozzuk az egymás után következő számokat csökkenő sorrendben, azt faktoriálisnak hívjuk és az összeszorzandók közötti legnagyobb szám után írt felkiáltójellel jelöljük. Jelen esetben az 5 x 4 x 3 x 2 = 5!
Azt a módszert, ahogy a fent leírt módszerrel leültettem a gyerekeket, permutációnak hívjuk és P betűvel jelöljük. Jelen esetben ez ismétlés nélküli permutáció, hiszen egy gyerek egyszerre csak egy székre tud leülni és ha egyszer leült, akkor már nem állhat fel. Általánosabban megfogalmazva n darab dolog ismétlés nélküli permutációja

Lépjünk eggyel tovább és nézzük meg, mi történik akkor, ha nem öt gyereket akarunk leültetni az öt darab székre, hanem egy 30 fős osztályt!

Tehát a feladat az, hogy a 30 fős osztályból hányféle módon tudunk kiválasztani öt gyereket, akiket sorban leültetünk az öt székre. A gondolatmenet hasonló, mint a permutáció esetében:
- Az első székre 30 gyereket tudunk kiválasztani, tehát 30-féle módon tudunk kiválasztani egy gyereket, aki az első székre ül.
- A második székre már csak 29 gyerek közül tudunk kiválasztani egyet, mert az első székre egyet már leültettünk, tehát az első két székre összesen 30 x 29 = 870 különböző lehetőségünk van leültetni a gyerekeket.
- A harmadik székre így 28, a negyedik székre 27, az ötödik székre pedig 26 különböző módon tudjuk kiválasztani, hogy melyik gyerek üljön oda.
Tehát az eredmény 30 x 29 x 28 x 27 x 26 = 17 100 720, tehát több, mint 17 millió különféle variáció adódik. Egy dolgot azonban ne felejtsünk el. Előfordulhat az az eset, hogy Aladár ül le az első székre és Beáta a másodikra, de az is, hogy Beáta ül az első székre és Aladár a másodikra. Ez azt jelenti, hogy ez esetben számít, hogy a gyerekek milyen sorrendben ülnek le mert - ha Aladár ül az első székre és Beáta a másodikra, az NEM ugyanaz az eset, mintha Beáta ül az első székre és Aladár a másodikra. Ezt a fajta kiválasztást, amikor a kiválasztott elemek sorrendje is számít, variációnak nevezzük, és V betűvel jelöljük. Így, ha n darab dologból k darabot szeretnénk kiválasztani úgy, hogy a sorrend számít, akkor ezt úgy számolhatjuk ki, hogy

Ezt a komoly matematikusok (aki én nem vagyok) egy más formára szokták hozni, hogy általánosabb rendeltetésű legyen (az átrendezés szépen levezethető, de ezzel most nem fárasztanálak):
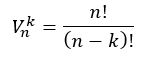
És akkor most térjünk rá a harmadik esetre, ami csak abban különbözik a variációtól, hogy ez esetben nem számít a kiválasztott elemek sorrendje, tehát maradva az előző példánál, ha Aladár ül az első székre és Beáta a másodikra, az UGYANAZ az eset, mintha Beáta ül az első székre és Aladár a másodikra. Ezt kombinációnak hívjuk és C betűvel jelöljük (a latin combinatio szó után). Visszatérve az előző példánkhoz, ha nem akarjuk figyelembe venni a kiválasztott elemek sorrendjét, akkor a 30 x 29 x 28 x 27 x 26 szorzatot el kell osztanunk annyival, ahányféleképpen sorba tudjuk rendezni az öt kiválasztott gyereket, azaz 2*3*4*5-tel!
Nos, mit kell tennünk ahhoz, hogy a variációtól eljussunk a kombinációig? Mivel itt láttuk, hogy a kiválasztott elemek sorrendje itt nem számít, ezért bármilyen sorrendben választjuk ki az elemeket, az mind ugyanaz az eset! Ezek szerint a variáció értékét el kell osztanunk a kiválasztott elemek összes lehetséges sorrendjével (ismerős?), azaz a kiválasztott elemek permutációjával! Tehát ezt felírhatjuk úgy is, hogy
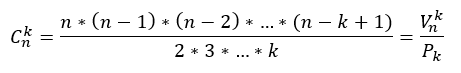
A komoly matematikusok ezt szintén másképpen írják:
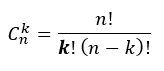
Ebben a képletben is látható, hogy a kombináció csak annyiban különbözik a variációtól, hogy itt a nevezőt megszorozzuk k!-al. Érdekesség, hogy ezt a kombinációt a Pascal-háromszög segítségével is megkaphatjuk, de ezt most nem ismertetném itt részletesen, mert ez a videó sokkal jobban elmagyarázza a Pascal-háromszög magyarázatát és használatát.
Amikor elénk kerül egy feladat, amit kombinatorikai módszerekkel kell megoldanunk, akkor érdemes a következő kérdéseket feltennünk magunknak:
1. Sorba kell rendezni az elemeket, vagy ki kell választani az elemek halmazából valamennyi számot?
Ha sorba kell rendezni az elemeket, tehát n megegyezik k-val, akkor biztos, hogy permutációról van szó. Ha k kisebb, mint n, akkor a következő kérdés az, hogy
2. Számít-e a kiválasztott elemek sorrendje?
Ha igen, akkor variációról van szó, ha nem, akkor pedig kombinációról
Vegyük példaként a lottószám sorsolást. Itt 90 szám közül kell kiválasztani ötöt, tehát k kisebb, mint n, azaz nem sorba rendezési, hanem kiválasztási problémáról van szó. Mivel a lottószám sorsolás esetében NEM számít a számok sorrendje, tehát itt kombinációról van szó. Erről részletesen írtam itt.
Természetesen a kombinatorika tudományát is a végletekig el lehet bonyolítani, ennek a bejegyzésnek csak annyi célja volt, hogy az olvasót a legfontosabb alapokkal képbe hozza. Remélem nem volt sikertelen a próbálkozás.





