Egy napon összejöttök a haverokkal és elmentek bowlingozni. Alig kezdtek el játszani, az egyik haverod, Samu kijelenti, hogy ő eszméletlenül jó nagyon erős játékos, hosszú ideje átlagosan 150 pontot szokott dobni meccsenként. 150 pont a bowlingban nagyon jó eredménynek számít, általában a profi játékosok szoktak ilyen eredményeket elérni. Azt mondod: rendben, tegyünk egy próbát! Lejátszotok három kört és Samu átlaga a három kör alatt egy kiábrándító 40 lett. Egy ilyen helyzetben elhiszed neki, ami állít?

Valószínűleg nem hiszel neki, hiszen aki hosszú idő alatt egyenletesen képes 150 körüli átlagot hozni, az tényleg nagyon jó játékos, tehát valószínűtlen, hogy hirtelen csak 40-et képes dobni. Azaz Samu haverod egy kicsit nagyképű…

Most viszont képzeljük el ugyanezt a szituációt egy kicsit más végeredménnyel. Tegyük fel, hogy Samu a három kör alatt átlagosan 140 pontot teljesít. Ebben a szituációban sokkal inkább hajlamos vagy elhinni, amit Samu állít, hiszen a 140 pont egészen közel van a Samu által ígért 150 ponthoz. Ráadásul amikor Samu azt állítja, hogy az eredménye átlagosan 150 pont, az nem azt jelenti, hogy minden egyes mérkőzésen 150 pontot fog dobni, hanem azt, hogy némelyik mérkőzésen többet dob, máskor meg kevesebbet. Lehet, hogy most éppen kifogott egy kicsivel rosszabb formát, vagy éppen csak pechje volt, de ez alapján még hihető, hogy Samu tényleg ennyire jó játékos.

A lényeg az, hogy annál inkább hajlamos vagy elhinni Samunak, hogy képes a 150 pontos átlagra, minél közelebb lesz az általa három kör alatt dobott pontok átlaga ehhez az értékhez.  

Igazából két szélsőséges szituációról beszélgetünk: Az egyik, amikor Samu 40 pontot és a másik, amikor 140 pontot dobott. Az első esetben Samu fejére olvasod, hogy hazudik és ezzel vége a barátságnak, a másik esetben pedig elfogadod a kijelentését és továbbra is barátok maradtok. Ezekben az esetekben relatíve egyszerű döntést tudunk hozni arról, hogy Samu igazat mond-e, avagy hazudik. A kérdés viszont az, hogy mennyi az a pontszám, amikor még elhiszed, hogy Samu jó játékos, és mikor mondod rá, hogy hazudik? Noha az egy eléggé szubjektív kérdés, hogy neked éppen mennyi az a pontszám, aminél még elhiszed, hogy Samu tényleg igazat mond, azért képes vagy magadban kialakítani egy véleményt arról, hogy nálad mennyi ez a határ.

Tételezzük fel, hogy ha Samu a három játék átlagában kevesebbet hoz 120 pontnál, akkor nem hiszel neki, ha viszont többet csinál 120 pontnál, akkor pedig elhiszed, ami állít. Ez így persze egy erősen szubjektív vélemény, de ettől ez még egy döntés.

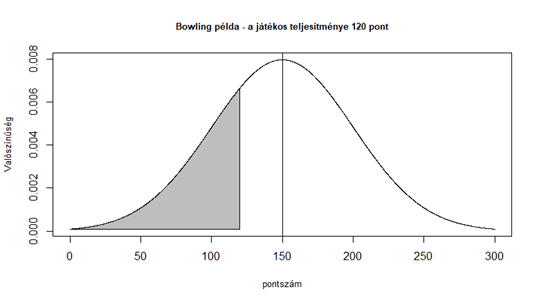
A diagramon lévő szürke terület nagysága azt adja meg, hogy mekkora a valószínűsége annak, hogy Samu fejéhez vágod, hogy hazug. Ez most egy eléggé jelentős méretű terület.

Ez eddig rendben is van, de most csavarjunk egyet a helyzeten: Tegyük fel, hogy édesanyád egy vagány és sportos hölgy, aki nagyon szeret bowlingozni. Ma van a születésnapja, ezért megszervezed, hogy együtt elmenjetek bowlingozni egyet. Már régen nem voltatok együtt játszani, így nem tudod, hogy mennyire jó játékos, ezért nem ismered a jelenlegi játéktudását, de ő azt mondja, hogy már hosszú idő óta egyenletesen 150 pont körül teljesít. Lezajlik a három játszma és édesanyád teljesítménye a kiábrándító 40 pont körül alakul. Ez ugye egy eléggé kellemetlen helyzet, hiszen a saját édesanyádnak nem mondhatod csak úgy, hogy hazug és nem hiszed el, hogy ő annyira jó játékos, mint ahogy azt állítja.

Természetesen ugyanígy megtörténhet az is, hogy az édesanyád 140 pontot dob átlagosan a három játék alatt és így könnyen hihető, hogy képes ennyire jól játszani. Tehát itt is megvan a két szélsőséges helyzet, de a szituáció mégis egy kicsit más. Az ember a saját édesanyját nehezebben vádolja meg azzal, hogy hazudik, szóval egy kicsit óvatosabban kell eljárni. Ha a helyedben lennék, én lehet, hogy nem 120-nál, hanem mondjuk 50-nál húznám meg a határt, ami alatt azt mondom, hogy anya hazudik (de lehet, hogy még akkor sem merném neki megmondani). Szóval a döntésnek nagy a tétje, ezért nyilvánvalóan nem leszel annyira szigorú, mint a haveroddal, de azért itt is van egy pont, ahol azt mondod, hogy azért ezt már mégsem hiszed el.

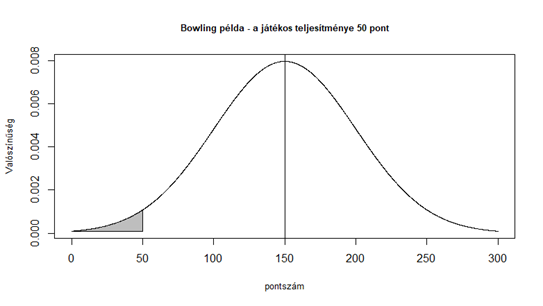
Amint az jól látható, a diagram szürke zónája sokkal kisebb, tehát jelentősen kisebb annak az esélye, hogy édesanyád fogod hazugnak nevezni.

Szóval nagyjából erről szól a hipotézis vizsgálat. A hipotézis szó görög eredetű és egy olyan feltevést vagy feltételezést jelent, amely még nincs bizonyítva. A hipotézis vizsgálat során tulajdonképpen bizonyítani próbálunk egy olyan feltevést vagy feltételezést, amely még nincs bebizonyítva. Rengeteg különféle hipotézis vizsgálat létezik, de a vizsgálat menete szinte mindegyik vizsgálati módszernek ugyanaz:

1. Megfogalmazzuk, hogy mi az a hipotézis vagy feltevés, amit bizonyítani akarunk. Ezt hívjuk nullhipotézisnek és jelöljük H0-al.
2. Megfogalmazzuk, hogy mi az ellenhipotézis, vagyis az előző pontban megfogalmazott feltevés ellentéte (ezt H1-el jelöljük). Mi az igaz akkor, ha az előző feltevés nem igaz?
3. Egy minta alapján megvizsgáljuk, hogy igaz-e a feltevésünk.
4. Ha a minta azt mutatja, hogy a feltevésünk igaz, akkor elfogadjuk a nullhipotézist és elvetjük az ellenhipotézist.
5. Ha a minta azt mutatja, hogy a feltevésünk hamis, akkor a nullhipotézist elvetjük és az ellenhipotézist fogadjuk el.

Azt, hogy mennyire akarunk biztosak lenni a döntésünk helyességében, megbízhatósági (avagy konfidencia) szintnek szoktuk elnevezni. Általában azt szoktuk mondani, hogy 95%-os biztonsággal szeretnénk kijelenteni, hogy a döntésünk, hogy elfogadjuk-e a nullhipotézist vagy elutasítjuk, azaz 5% hibázási lehetőséget fenntartunk magunknak. Ha nagyon biztosak akarunk lenni a dolgunkban, akkor nem 95%-os, hanem 99%-os megbízhatósági szintet határozunk meg.

Itt még beszélnünk kell a döntéseink következményeiről:

Vegyük most példaként Samu esetét:

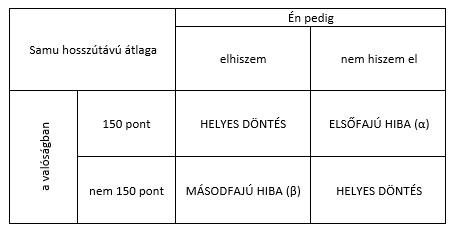
Nézzük, milyen esetek fordulhatnak elő:

1. Samu hosszútávú átlaga a valóságban 150 pont, én pedig elhiszem neki, hogy 150 pont az átlaga. Ez egy helyes döntés.
2. Samu hosszútávú átlaga a valóságban nem 150 pont, én pedig nem hiszem el neki, hogy 150 pont az átlaga. Ez is egy helyes döntés.
3. Samu hosszútávú átlaga a valóságban 150 pont, én viszont nem hiszem el neki, hogy 150 pont az átlaga.Ez egy hibás döntés, és a következményei súlyosak, hiszen összeveszek Samuval, noha igazat állít. Ezt elsőfajú hibának nevezzük és α-val jelöljük.
4. Samu hosszútávú átlaga a valóságban nem 150 pont, de én elhiszem neki, hogy 150 pont az átlaga. Ez szintén egy hibás döntés, viszont ennek kevésbé súlyosak a következményei, hiszen igaz, hogy Samu a valóságban nem játszik jól, és sikerült "becsapnia", viszont legalább nem vesztünk össze és barátok maradtunk. Ezt másodfajú hibának nevezzük és β-val jelöljük.

A célunk nyilvánvalóan az, hogy minél nagyobb eséllyel hozzunk helyes döntéseket és minél kisebb valószínűséggel hibás döntéseket. Ezen belül is – ha már hibázunk - természetesen azokat a hibákat tartjuk inkább elfogadhatónak, amelynek kevésbé súlyosak a következményei, tehát lehetőleg úgy tévedjünk, hogy az elsőfajú hiba előfordulásának valószínűsége legyen nagyobb és másodfajú hibát lehetőleg ne is kövessünk el.

Meg kell még említenem egy dolgot, ami természetesen egy kicsit még tovább bonyolítja a képet. A hipotézis vizsgálatok esetében szoktunk egyoldali, illetve kétoldali ellenhipotézisről beszélni. Egyoldali ellenhipotézis lehet baloldali és jobboldali is. Mit jelent ez részletesen?

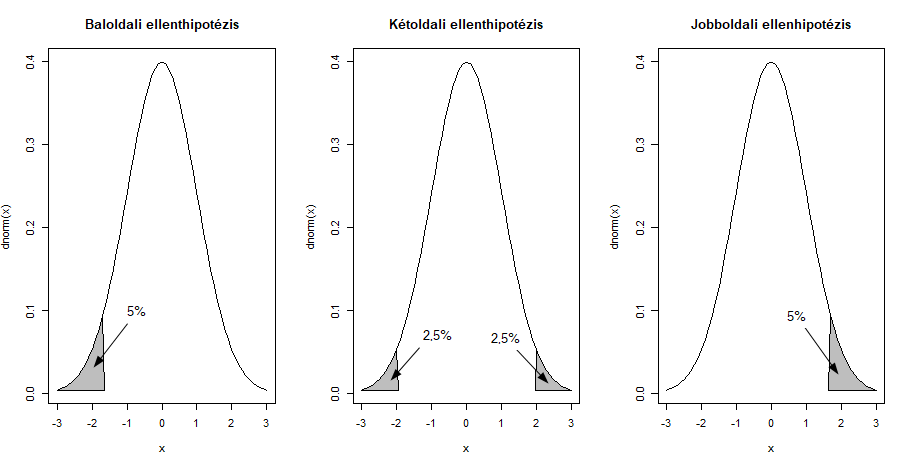
Tegyük fel, hogy 95%-os biztonsággal akarunk dönteni. Ez azt jelenti, hogy van egy 5%-os hibatartományunk, amit eloszthatunk annak a függvényében, hogy milyen típusú hibára számítunk:

• Ha arra számítunk, hogy a mintánk átlaga KISEBB lesz, mint a sokaság átlaga, akkor BALOLDALI ELLENHIPOTÉZIS-ről beszélünk. Ekkor úgy számítjuk ki a teszt határértékét, hogy az 5%-os valószínűség a BAL oldalon legyen.
• Ha arra számítunk, hogy a mintánk átlaga NAGYOBB, mint a sokaság átlaga, akkor JOBBOLDALI ELLENHIPOTÉZIS-ről beszélünk. Ekkor úgy számítjuk ki a teszt határértékét, hogy az 5%-os valószínűség a JOBB oldalon legyen.
• Ha NEM TUDJUK, hogy a mintánk átlaga kisebb vagy nagyobb lesz, akkor KÉTOLDALI ELLENHIPOTÉZIS-t alkalmazunk, ekkor 2,5% - 2,5%-ot teszünk mindkét oldalra.

Ez a lecke talán egy kicsit hosszúra sikerült és elég sok mindent szuszakoltam bele, de remélem így is érthető lesz.