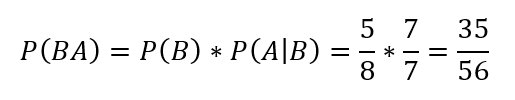A múlt héten belevágtam egy nagyobb témába a feltételes valószínűségről (Választás velencei módra – A feltételes valószínűségről). Azért valljuk be, az előző bejegyzés inkább csak kedvcsinálónak volt jó, sok lényeges dolgot nem tudtunk meg belőle. Pedig a téma messzire vezet, de addig még keresztül kell botorkálnunk pár kapcsolódó nehézségen.
Az előző cikkben egy szemléletes példa alapján próbáltam bemutatni, hogy mit is jelent a feltételes valószínűség fogalma. Akkor beszélünk feltételes valószínűségről, ha egy A esemény bekövetkezésének esélye függ egy másik B esemény eredményétől, vagyis az A esemény valószínűsége annak függvényében változik, hogy a B esemény eredménye milyen lesz. Ezt jelöljük úgy, hogy
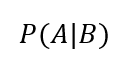
ezzel a fura függőleges vonallal az A és a B között. Ez nem ugyanaz, mint a
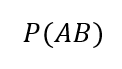
amely az A és a B események együttes bekövetkezésének valószínűségét jelzik. Nézzük meg ezt egy egyszerű példán keresztül. Tegyük fel, hogy van egy zsákunk, amelyben van 5 darab fehér és 3 darab piros golyó.
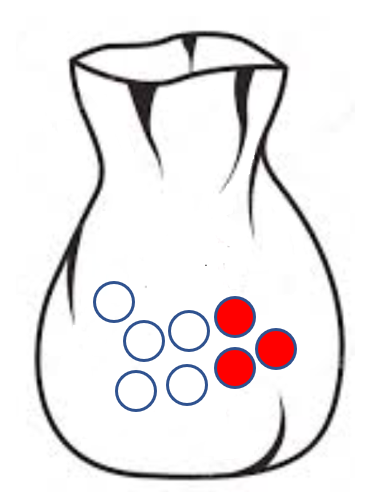
Legyen az A esemény az, hogy piros golyót, a B esemény pedig az, hogy fehér golyót húzunk ki. Ebben a felállásban 3/8 az esélye annak, hogy elsőre piros golyót húzunk ki és 5/8 az esélye annak, hogy elsőre fehér golyót húzunk. A második húzás már egy kicsit trükkösebb. Ha az első húzás eredménye piros volt, akkor a zsákban maradt 5 fehér és 2 piros golyó. Így 5/7 az esélye, hogy a második húzásra fehér golyót húzunk majd, illetve 2/7 az esélye annak, hogy pirosat. Ha viszont elsőre fehéret húztunk, akkor 4 fehér és 3 piros golyónk maradt a zsákban, így a második húzásra 4/7 lesz az esélye a fehér golyó és 3/7 lesz az esélye a piros golyó kiválasztásának.
Ez a leírás egy kicsit kuszának tűnik, ezért megpróbálom egy kicsit plasztikusabban bemutatni ezt a levezetést:

Remélem, valamivel jobb. De még csak most jön a neheze!
Ismételjük át az eddigieket. Az A esemény – azaz P(A) - az, ha piros golyót húzunk, a B esemény – P(B) – pedig az, ha fehéret. Azt is tisztáztuk már korábban, hogy az A esemény valószínűsége az első húzásra 3/8. Tegyük fel, hogy elsőre piros golyót húztunk ki a zsákból, majd második húzásra egy fehéret. Ennek a valószínűsége 5/7, ahogy az az alábbi ábrán is látszik.
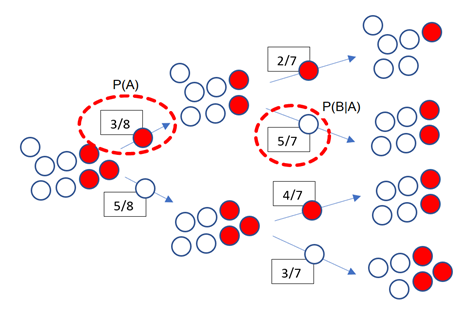
Nézzük meg a másik esetet is. Ez alapján az első húzásra fehér golyót húztunk – ennek a valószínűsége P(B). Ez az esemény 5/8 valószínűséggel fog bekövetkezni. Ha az első húzás fehér volt, akkor annak az esélye, hogy másodszorra piros lesz pontosan 4/7 lesz.
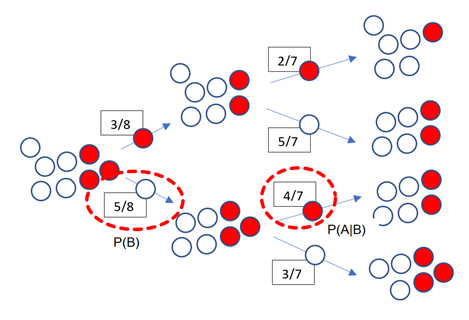
Ez mind érdekes, de a legérdekesebb ebben az egészben az, hogy mindkét esetben egy fehér és egy piros golyót választottunk ki a 8 golyó közül. Egy korábbi bejegyzésben már tisztáztuk (Gyakoribb-e a kék szem a szőkék között? – Khí-négyzet próba a függetlenség vizsgálatára), hogy ha az A és a B esemény valószínűsége független lenne, akkor a két esemény bekövetkezésének együttes valószínűsége megegyezik az A esemény és a B esemény valószínűségének szorzatával, azaz

Jelen esetben viszont a B esemény valószínűsége NEM független az A esemény valószínűségétől. Mivel általánosságban igaz, hogy egy összetett esemény valószínűsége megegyezik az elemi események valószínűségének szorzatával, a fenti levezetésből adódik, hogy
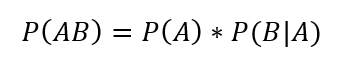
illetve
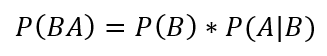
Visszatérve a konkrét példára, P(AB) annak a valószínűsége, hogy a zsákból először egy piros golyót húzunk ki, majd utána egy fehéret, P(BA) pedig annak a valószínűsége, hogy először egy fehér golyót húzunk ki, és utána egy pirosat. Végül számoljuk ki P(AB) és P(BA) értékét:
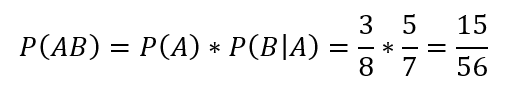
illetve