
A Velencei Köztársaság a mediterrán Európa egyik legbefolyásosabb hatalma volt a VIII. és a korai XVIII. század között. Noha sok helyen városállamként emlékeznek meg róla a krónikák, szerepe ennél lényegesen nagyobb volt. Flottája és fejlett haditechnikája révén döntő befolyásra tett szert az Adria jelentős részén, amely még Kréta és Ciprus szigetét is magában foglalta. A velencei városállamban tulajdonképpen a nagytanács gyakorolta a hatalmat, amely 300-400 rangos velencei polgárból állt. A nagytanács élén állt a dózse, akit szavazással választottak meg. 697-től 1797-ig több, mint 150 dózse állt Velence élén. Volt, aki csak pár hónapig, de egyvalaki több, mint 34 évig uralkodott. Ez a bizonyos választás érdekes tanulságokkal szolgál a valószínűségszámítással kapcsolatban is.

A velencei városállamot tulajdonképpen a nagytanács gyakorolta a hatalmat, amely 300-400 rangos velencei polgárból állt. A nagytanács élén állt a dózse, akit szavazással választottak meg. 697-től 1797-ig több, mint 150 dózse állt Velence élén. Volt, aki csak pár hónapig, de egyvalaki több, mint 34 évig uralkodott.
Ez a szavazás igencsak érdekes módon zajlott. Amikor valamilyen ok miatt új dózsét kell választani, a nagyhatalmú családok tagjai közül kiválasztottak néhányat, akik aztán kiválasztottak egy nagyobb csoportot maguk mellé- Aztán ebből a nagyobb csoportból ismét kiválasztásra került egy kisebb csoport, amely kiválasztott egy nagyobb csoportot, és így tovább, amíg ki nem alakult egy olyan csoport, aki végül megválasztotta a dózsét. A gyakorlatban ez úgy nézett ki, hogy gyúrtak 30 viaszgolyót és minden viaszgolyóba beletettek egy-egy darab papírt. Ezeknek a papíroknak a nagy része üres volt, csak 9 darabra volt ráírva a „lector” szó. Aki ilyen papírt tartalmazó golyót húzott ki, az bekerült a kiválasztottak közé és választhatott maga mellé társakat, összesen 40-et. Ez a 40 újabb kiválasztott aztán hasonló sorsolással kiválasztott 12-őt, akik …
A folyamatban jelen esetben a viaszgolyók kihúzása az érdekes. Az első jelölt, aki választ a viaszgolyók közül, 9/30 valószínűséggel fog olyan viaszgolyót húzni, amelyben a papíron szerepel a „lector” szó. A második jelölt esetében ez már nem ennyire nyilvánvaló; mert, ha az első jelölt olyan viaszgolyót húz, amelyikben szerepel a „lector” szó a papíron, akkor a második jelöltnek 8/29-ed esélye van arra, hogy jelöltté váljon. Abban az esetben viszont, ha az első jelölt üres papírt tartalmazó viaszgolyót húz ki, akkor a második jelölt esélye 9/29 lesz! A különbség talán nem tűnik olyan nagynak, de ettől még az elv érvényes: A második jelölt esélye arra, hogy lector-rá váljon függ attól, hogy az első jelölt húzásának mi volt az eredménye.
Ezt a jelenséget nevezzük feltételes valószínűségnek. Általánosabban fogalmazva a feltételes valószínűség azt jelenti, hogy esemény bekövetkezésének valószínűsége az azt megelőző esemény eredményének függvényében változhat.
Sajnos nem tudom elkerülni, hogy bevezessek egy újabb „mágikus jelet”, a feltételes valószínűséget a következő módon jelöljük:
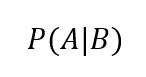
Ez azt jelenti, hogy az A esemény valószínűsége a B esemény bekövetkezésének függvényében változik, a feltételes valószínűséget a zárójelen belül az A és a B közötti függőleges vonal jelöli.
források:
David Salzburg: The lady tasting tea, Henry Holt and Company LLC, New York 2001
Mary McCarthy: Velence közelről, Európa Könyvkiadó, Budapest, 1986.
The Chronicles of Venice: How the Doges Were Chosen
https://sourcebooks.fordham.edu/source/dogesvenice.asp




