
A napokban a kollégáimnak próbáltam elmagyarázni az egymintás Z-próba lényegét és rájöttem, hogy nem igazán tudom értelmesen elmagyarázni, hogy mi is az a hipotézis vizsgálat és miért kell ezt pont úgy csinálni, ahogyan azt csináljuk. Állati régóta töröm ezen a fejem, de eddig még nem sikerült igazán plasztikusan megvilágítani a probléma lényegét. Most újra megpróbálok nekifutni a dolognak…
A történet újra ott indul, hogy van egy populáció, amelyet meg szeretnénk ismerni, de ez komoly akadályokba ütközik, a sokaság teljes megismerése valamilyen ok miatt lehetetlen. Képesek vagyunk a sokaságból mintát vagy mintákat venni, meg tudjuk vizsgálni a minták tulajdonságait és ez alapján képesek vagyunk következtetni bizonyos dolgokra. Azt azonban még véletlenül sem lehet kijelenteni, hogy a sokaság tulajdonságai megegyeznek egy abból kivett minta tulajdonságaival. A minta tulajdonságai csakis önmagára vonatkoznak. Ha veszünk a populációból egy másik mintát, annak már más tulajdonságai lesznek, pedig ugyanabból a sokaságból vettük ki őket. Ezt próbáljuk ki, mert el kell hinnünk, hogy ez így van. Készítsünk 10 cetlit, a cetliket számozzuk meg egytől tízig és dobjuk bele őket egy kalapba.
pelda <- c(seq(1:10))
pelda
A parancsok hatására a következő eredményt kapjuk:
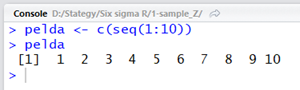
Mivel most az a cél, hogy mindent R-ben mutassak be, ezért a fenti példát is R-ben készítem el. A fenti kód egy kissé kínainak néz ki, de igazából nem bonyolult. Megkértem az R-t, hogy hozzon létre egy ’pelda’ nevű változót. A ’c()’ függvény használatával létre lehet hozni bármilyen sorozatot, legyen az számok, szövegek, logikai értékek, illetve ezek keverékeinek sorozata. A ’seq()’ függvény segítségével pedig szekvenciákat lehet készíteni, vagyis a jelen esetben alkalmazott ’seq(1:10)’ létrehozza számok sorozatát egytől tízig. Így a fenti kód azt az utasítást adja a fordítónak, hogy hozza létre számok sorozatát egytől tízig és ezt helyezze el a ’pelda’ nevű változóba. Ha ezekután egyszerűen begépeljük a változó nevét, az R ki fogja írni a tartalmát.
Következő lépésként vizsgáljuk meg a ’pelda’ tulajdonságait.
atlag <- mean(pelda)
szoras <- sd(pelda)
atlag
szoras
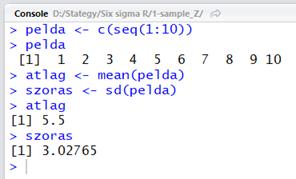
Tehát a ’pelda’ adatsor átlaga 5,5, szórása pedig körülbelül 3. Most vegyünk ki a kalapból becsukott szemmel három cetlit.
minta1 <- sample(pelda, size = 3, replace = TRUE)

Az első minta a hatot, a kettőt és a négyet tartalmazza. Ennek a három elemű mintának az átlaga 4, szórása pedig 2. A mintának sem az átlaga, sem a szórása nem egyezik meg a ’pelda’ nevű adathalmazzal, pedig abból vettük ki. Most vegyünk ki egy másik három elemű mintát a ’pelda’ adatsorból!
minta2 <- sample(pelda, size = 3, replace = TRUE)
minta2
atlag2 <- mean(minta2)
szoras2 <- sd(minta2)
atlag2
szoras2

Természetesen a második minta tulajdonságai még véletlenül sem egyeznek meg a ’pelda’ adatsor, vagy az első minta tulajdonságaival. Ezzel sikerült teljesen elveszíteni a talajt a lábunk alól. Ott tartunk, hogy van a kezünkben egy minta és a minta vizsgálatából szeretnénk megtudni valamit a sokaságról. De melyik sokaságról? Honnan tudjuk, hogy a mintát éppen melyik sokaságból vettük ki?
Hogyan? Nemcsak egy sokaságunk van? A gyakorlatban valószínűleg tényleg csak egy van, de elméletileg akár végtelen számú különböző sokaságot is el tudunk képzelni, hiszen a vizsgálandó sokaságunk tulajdonságairól nem tudunk SEMMIT! Az első mintában kapott 6-ot, 2-őt és 4-et kivehettük volna a következő tíz számból is.:
2, 4, 6, 8, 10, 12, 14, 16, 18, 20
vagy ebből is:
2, 3, 4, 5, 6, 7, 8, 9, 10, 11
De miért lenne igaz, hogy egy szám csak egyszer szerepel a sokaságban?
2, 4, 6, 2, 4, 6, 2, 4, 6, 2
Sőt, az sem szükségszerű, hogy 10 cetli van a kalapban, hogy az összes papírdarabra pozitív egész szám van írva, sőt még az sem, hogy az összes papíron szám szerepel, és így tovább…
Azon persze lehetne vitatkozni, hogy a fent említett 6, 2 és 4 melyik adatsor esetében hány mintavételből hányszor jönne ki, de mivel fogalmunk sincs, hogy hány cetli van a kalapban és mi is van tulajdonképpen rájuk írva, ez megint csak nem visz sehova. Talán az, ha nagyon sok mintát vennénk a kalapból és megszámolnánk, hogy hány esetből hányszor jön ki pont a 6, a 2 és a 4…
Fogadjuk el, hogy nem tudjuk, hogy mi van a kalapban és kész. Tulajdonképpen két dolgot tudunk megmondani a mintavétel eredménye alapján. Az egyik az, hogy a kalapban biztosan van egy olyan cetli, amire 6, egy másik, amire 2 és egy harmadik, amire 4 van írva.
A másik az, ami érdekes a számunkra. Az, hogy kizárhatjuk az összes olyan lehetséges esetet, amikor a kalapban lévő cetlik között nincs legalább három olyan cetli, amelyek közül az egyikre 6, a másikra 2, a harmadikra pedig 4 van írva! Vagyis az nem lehet, hogy a cetlik például így vannak megírva:
1, 3, 5, 7, 9, 11, 13, 15, 17, 19
vagy így:
1, 3, 5, 1, 3, 5, 1, 3, 5, 1
vagy így:
január, február, március, április, május, június, július, augusztus, szeptember, október, november, december
És ezt megint csak a végtelenségig lehetne folytatni.
Tehát két végtelen sok elemből álló halmaz áll egymással szemben. Az egyik azoknak a potenciális sokaságoknak a halmaza, amelyekből a mintát kivehettük, a másik pedig azoknak a sokaságoknak a halmaza, amelyekből nem.
Akkor a fentiek alapján mi az egyetlen dolog, amit biztosan be fogunk tudni bizonyítani a minta alapján? Nem az, hogy mi van, hanem az, hogy mi NINCS a kalapban!
Ha a kihúzott három cetlire a 6, a 2 és a 4 van ráírva, akkor biztosak lehetünk abban, hogy mely a cetliknek mely kombinációi NINCSENEK a kalapban. A végtelen sok lehetőség közül kizárhatjuk azokat, amelyekben nincs benne legalább egyszer a 6, a 2 és a 4. Hurrá, még mindig végtelen sok cetli kombináció maradt…
Emiatt folyamodunk ahhoz a módszerhez, hogy felállítunk egy hipotézist, azaz kitalálunk egy feltételezést. Például azt mondjuk, hogy a kalapban lévő egyik cetlire sincs ráírva a hetes szám. Ez lesz a nullhipotézisünk. Kihúzzuk az első mintát, a cetliken szereplő számok a már megszokott 6, a 2 és a 4. Jó, akkor most fellélegezhetünk, elfogadjuk a nullhipotézist, majd elégedetten szürcsölünk egyet a teánkból… Ja, nem.
Merthogy az rendben van, hogy a három kihúzott cetlin nincs hetes szám, de fogalmunk sincs arról, hogy azokon a cetliken, amely benne maradtak a kalapban, vajon nem-e szerepel legalább egy hetes. Vagyis attól, hogy elfogadtuk a nullhipotézist, semmivel sem lettünk boldogabbak. Sajnos ebben az esetben nem mondhatjuk azt, hogy elfogadtuk a nullhipotézist – vagyis azt, hogy a kalapban nincs 7-es – csak annyit jelenthetünk ki, hogy
nincs elegendő bizonyítékunk arra vonatkozóan, hogy a kalapban nincs 7-es egyik cetlin sem!
Mi történik akkor, ha a második mintát húzzuk ki a cilinderből, a 7-et, a 3-at és az 1-et? Mivel a mintában volt egy olyan cetli, amelyen a 7-es szám szerepel, ezért a nullhipotézist elvetjük és az ellenhipotézist fogadjuk el, vagyis
biztosan állíthatjuk, hogy a kalapban NEM LEHET olyan számsorozat a cetliken, amelyek közül egyik sem 7!
Vagyis a hipotézis vizsgálat célja nem egy állítás igazolása, hanem pont ellenkezőleg! Az a cél, hogy bebizonyítsuk egy állításról, hogy az nem igaz.
A történet nagyon fontos tanulsága az, hogy ha a hipotézis vizsgálat eredményeként nem sikerül elvetni a nullhipotézist, akkor a teszt eredményeként csak annyit tudunk leírni, hogy nincs elegendő bizonyítékunk arra, hogy a nullhipotézist el tudjuk vetni. Vagyis például egy számítási feladat esetében is egy hasonló szöveges értékeléssel kell kiegészíteni a feladat megoldását.
Nem egy könnyű téma... :-)





