Úgy tűnik, nem tudok elszakadni a témától. Már az előző cikk (Senki többet harmadszor? – Újra az egymintás Z-próbáról, most R-kóddal) írása közben motoszkált a fejemben, hogy a próba egyszerűsége ellenére jó lenne valahogy vizuálisan is megjeleníteni az eredményt. Neki is ugrottam, hogy készítek egyet, de aztán a kód csak hízott és hízott, úgyhogy arra jutottam, hogy írok erről egy külön cikket. Mivel az R-kód hossza nincs arányban a fontosságával, ezért a diagram kirajzolását függvényként írtam meg, így a diagram kirajzolása 2-3 sor begépelésével megoldható. Másrészt a szkript részletes elemzéséből ismét sokat lehet tanulni.

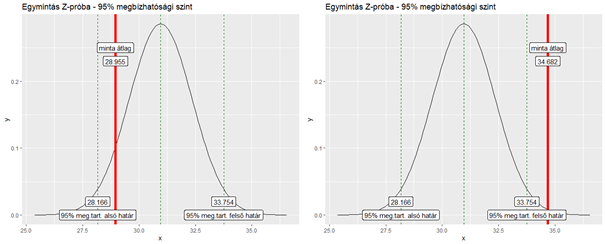
A cél az, hogy láthatóvá tegyük az egymintás Z-próba eredményét. A fenti diagramon látható normál eloszlás görbe a sokaságból elméletileg kivehető nagyszámú minta átlagainak az eloszlását reprezentálja. A két függőleges szaggatott vonal határolja azt a tartományt, amelybe a mintaátlagok 95%-a esne. A tesztünk nullhipotézise az, hogy az általunk vizsgált mintát a megadott átlag és szórású sokaságól vettük ki. A vastag piros vonal az általunk kivett minta átlagát jelzi. Ha a vastag piros vonal beleesik a 95%-os tartományba, akkor a nullhipotézist el kell, hogy fogadjuk, azaz nem igazolható, hogy az általunk vizsgált mintát NEM a megadott átlagú és szórású sokaságból vettük ki. Ha a vastag piros vonal a 95%-os tartományon kívül esik, akkor viszont elvethetjük a nullhipotézist, azaz bizonyítékot találtunk arra, hogy a vizsgált mintát nem vehettük ki a sokaságból.

A teljes szkript egyben letölthető szövegfile-ként az alábbi linkről. A tömörített fájlban található egymintasztesztdiagram.R file-t R-ben vagy RStudio-ban megnyitva a szkript futtatható.

https://m.blog.hu/st/statisztikaegyszeruen/egymintasztesztdiagram.zip

A file tartalmazza a ’z.testgraph()’ függvényt, illetve azokat a kódsorokat is, amelyek segítségével teszteltem a függvény működését. Akkor nézzük részletesen, mit is csinál a program…

Először is töltsünk be három csomagot.

A sorok végén a # jel után rövid megjegyzéseket helyeztem el a jobb átláthatóság kedvéért. Amint azt ott is írtam, a függvény használatához csak a ’ggplot2’ csomag szükséges, a másik kettőt csak a kipróbáláshoz használtam.

A következő blokkban az előző cikkhez hasonlóan létrehoztam egy nagyon hasonló sokaságot, mint az előző cikkben, így a részletes ismertetéstől eltekintek.

Ezután kiszámoltam a létrehozott sokaság átlagát és szórását és elmentettem egy-egy változóba.

Mellékes megjegyzés: R-ben van egy olyan konvenció, hogy a változónevek első betűje kisbetű, de az összetett neveknél a második, harmadik stb. részeket nagybetűvel jelöljük. Ez nemcsak poénból van így, az RStudio-nak van egy olyan tulajdonsága, hogy amikor elkezdesz begépelni egy nevet, akkor a szerkesztő feldobja azokat a változókat vagy függvényeket, amelyek a begépelt karakterekkel kezdődnek. Így akár egy hosszabb változónevet is simán be tudsz gépelni pár billentyűleütéssel.

Ezekre majd akkor lesz szükség, amikor a diagram rajzoló függvényt hívjuk majd meg, hiszen a mintaátlagok eloszlásának becsléséhez szükség lesz a sokaság átlagára és szórására.

Ha a ’mean()’ és az ’sd()’ függvények használata esetleg nem egyértelmű, akkor ezt részletesebben megtalálod a „Six Sigma in R” sorozat – Leíró statisztika R-ben című cikkben.

Ezután létrehoztam kétféle mintát, hogy megmutassam a különféle mintaátlagok hatását az eredményre. A ’minta1’ változó egy olyan 100-elemű mintát tartalmaz, amelyet ugyan nem a korábban létrehozott sokaságból vettem ki, de elméletileg kivehettem volna belőle. A ’minta2’ változóban egy olyan minta van, amelyet biztosan nem vehettem ki a létrehozott sokaságból.

Remek megfigyelés, hogy a mintáknak csak az átlagát számoltam ki, a szórását nem, hiszen a minták szórására nem lesz szükségünk, hiszen ismerjük a sokaság szórását. Ezzel megvan mindenünk, a

És most következzen a függvény leírása.

A függvény megadása olyan, mintha egy változónak adnánk értéket. Ez olyannyira igaz, hogy a függvényt nem is tudjuk addig használni, amíg a kurzorral a sorra ráállva a CTRL-Enter billentyű kombináció lenyomásával le nem futtatjuk az értékadást és a függvény neve meg nem jelenik a változók között. Mondjuk ez a fajta függvénydefiníció logikusnak tűnik és nem kényelmetlen, csak egy kicsit meg kellett szokni. Természetesen a zárójelben megadott paramétereket kell majd átadni a függvénynek, amikor majd meghívjuk. A változóknak igyekeztem hosszabb „beszélő” nevet adni, hogy a kód könnyebben követhető legyen. Amint az látható, négy paramétert kell megadnunk. Az általunk kivett minta átlagát (mintaAtlag), a sokaság átlagát és szórását (sokasagAtlag, sokasagSzoras) és a minta elemszámát (n). A függvény törzsét kapcsos zárójelek közé kell tenni, ezért látható egy ’{’ a következő sorban.

A ’mintaEloszlasAtlag’ változó jelenti sokaságból elméletben kivett nagyszámú minta átlagát. Ezt a változót nem lett volna fontos létrehozni, de inkább létrehoztam, hogy jobban lehessen követni a kódot. A ’mintaEloszlasSzoras’ változó viszont a nagyszámú mintaátlag szórásának becsült értékét tartalmazza, amelyet ugye úgy kaptunk, hogy a sokaság szórását elosztottuk a minta elemszámának négyzetgyökével.

A mintaeloszlás tulajdonságainak segítségével kiszámoltam azt a tartományt, amelybe várhatóan beleesne a sokaságból kivett minták 95%-a. A ’ mintaEloszlas95Lower’ értelemszerűen az alsó, a ’mintaEloszlas95Upper’ a felső határt jelenti (igen, itt írhattam volna alsót és felsőt is, de csak most vettem észre, hogy véletlenül angol maradt az elnevezés. Bocs).

Ez a két sor technikai jellegű, a két változóba a diagramterület alsó, illetve felső határát tároltam el.

Ez a rész szintén technikai jellegű. Azért, hogy a diagramon megjelenhessenek a mintaátlag és a 95% megbízhatósági tartomány határainak értékei, a kiszámított értékeket szöveggé kell alakítani. Ráadásul azt úgy, hogy a tizedespont után ne legyenek tizedesjegyek kilométerhosszan. A szöveggé alakítást az ’as.character()’ függvény segítségével lehet elvégezni. A tizedesjegyek hosszának beállításához viszont a ’format()’ függvényt tudjuk használni. A ’format()’ függvény ’digits = 5’ paramétere azt mondja, hogy a számnak csak 5 számjegye jelenjen meg összesen, azaz az egész és a tizedes jegyek száma összesen 5 lehet. Ez nem biztos, hogy minden esetben szerencsés, mert például a egymillió felett ez már problémás lehet. Most így átgondolva, a ’format()’ függvénynek van egy ’nsmall’ nevű paramétere is, ezzel a tizedespont mögötti számok mennyiségét lehet beállítani. Igény szerint ez kicserélhető a kódban, vagyis a ’digits =5’ helyett az ’nsmall = 2’ is alkalmazható.

Most jön a lényeg, a diagram kirajzolása.

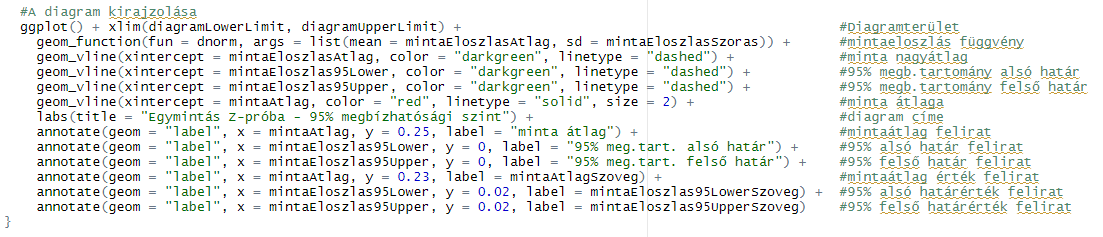
Ez a legösszetetteb kódrészlet, de csak elsőre tűnik vadnak, igazából az egész olyan, mint a legó, az egyes diagram elemeket szépen egymás után pakoltam. Az egyes elemeket a ’+’ jellel kötjük össze, ebből tudja a fordító, hogy ezek a kódrészletek összetartoznak. Nézzük meg soronként, hogy mi mit jelent.

A ’ggplot()1 függvény fogja össze a diagram egészét. Önmagában meghívva ez a függvény egy üres diagramterületet fog kirajzolni.

Az ’xlim()’ függvénnyel be tudjuk állítani az x-tengely mérettartományát.

 A ’geom_function()’ függvénnyel bármilyen függvénygörbét ki tudunk rajzoltatni. Természetesen vannak előre definiált függvénytípusok, amelyeket a ’fun =’ paraméter beállításával lehet megadni. Ez esetben ez a normál eloszlás sűrűségfüggvénye, ezért lett a ’fun =’ paraméter értéke ’dnorm’, ahol a d betű a ’density’, azaz sűrűség fogalmat takarja.

Nem elég megadni a függvény típusát, az adott függvény konkrét paramétereit is meg kell adnunk. Ezt az ’args =’ paraméter segítségével tudjuk megadni. Azért ilyen kacifántos, mert ahányféle függvénytípus, annyiféle paramétersort kell megadni a függvény pontos definíciójához. Az ’args =’ után egy listát kell megadnunk, amelyben benne vannak az egyes paraméterek, ez esetben az átlag (’mean =’) és a szórás (’sd =’). Mivel a diagramon a mintaátlagok eloszlását akarom megjeleníteni, ezért a normál eloszlás átlagának a mintaátlagok átlagát, azaz a sokaság átlagát adom meg, szórásának pedig a mintaátlagok szórását (lásd fentebb).

A ’geom_vline()’ függvény egy függőleges vonalat rajzol a diagramra, amely a diagramterület aljától a tetejéig tart, ezért nem kell megadni az y-irányú koordinátákat, csak az x-tengely metszéspontját az ’xintercept =’ paraméter megadásával.

A ’color = „darkgreen”’ a vonal színét adja meg, a ’linetype = „dashes”’ pedig a vonal mintázatát, jelen esetben a ’dashed’ a szaggatott vonalat jelöli.

A ’size = 2’ a vonal vastagságát adja meg.

Ez a sor írja ki a diagram címét a bal felső sarokba.

Az ’annotate()’ függvény segítségével mindenféle megjegyzéseket és jelzéseket tehetünk a diagramra egy szabadon választott helyre. Ez lehet egyszerű szöveg, pont, egyenes vagy görbe vonal, esteleg téglalap is. A megjegyzés típusát a ’geom =’ paraméterrel lehet megadni, ez esetben a ’geom = „label”’ azt jelenti, hogy egy bekeretezett címkét kell megjeleníteni. Itt vigyázni kell az idézőjelek alkalmazására, mert különben hibára futunk. Az x és az y-irányú koordináták megadása értelemszerű, a 0:0 pont a két koordinátatengely metszéspontjában van. A címke szövegét a ’label =’ paraméter után kell megadni idézőjelek között. A címke szövegét nemcsak közvetlenül adhatjuk meg, hanem egy szöveges változóra történő hivatkozással is, mint például az utolsó két sorban, ahol a már előzőleg elkészített szöveges változót adtam meg a címke felirataként.

Összegzés:

Ez a diagram véleményem szerint nem létszükséglet, de előfordulhat, hogy szükség van rá valamilyen jelentésben vagy prezentációban. Akadnak még továbbfejlesztési lehetőségek, például paraméterként át lehetne adni a megkívánt megbízhatósági szintet, vagy be lehetne színezni a megbízhatósági tartományt. Ha valakinek van ilyen igénye, akkor nyugodtan fejlessze tovább a függvényt a saját szükségletei és szájíze szerint. Sajnos a kódsorok hossza miatt a tördelés egy kicsit szétcsúszott, emiatt elnézést kérek.