
Ha a blog régi olvasója vagy, akkor már tapasztalhattad, hogy a sokaság és a minta kapcsolata már jó ideje foglalkoztat, de a téma jól érthető magyarázata eddig mindig problémát okozott. Már többféle módon is próbáltam megjeleníteni a sokaság és a minta mögött álló modellt, de ezek a próbálkozások eddig több kérdést szültek, mint valódi megértést. És egyszer csak végre megtaláltam téma jelenlegi Szent Grálját, egy olyan weboldalt, amely egyszerűen, különösebb sallangok nélkül, mégis látványosan mutatja be a sokaság és a minta kapcsolatának lényegét.
Tulajdonképpen nem is ezt kerestem, hanem a statisztikai teszteknél használt p-érték (A titokzatos P színre lép – Mi az a P-Value?) megbízhatóságával kapcsolatos problémák iránt kutattam, amikor rátaláltam erre az oldalra:
https://www.esci.thenewstatistics.com/esci-dances.html
Ez az oldal tulajdonképpen egy statisztika tankönyvhöz kapcsolódó vizualizáció. Sajnos a könyvet (lásd a források közt) eddig nem sikerült megszereznem, ráadásul ahol kapható, ott elég borsos az ára. Kárpótolt viszont, hogy az egyik szerzőnek, Geoff Cummins-nak van egy youtube-csatornája, ahol szépen artikulált angolsággal és a fent említett vizualizációk alkalmazásával magyaráz el egy csomó dolgot, amelyeket feltételezésem szerint a könyv is tartalmaz.
De lássuk, hogy hogyan is tudjuk használni a fenti oldalt. Érdemes egy másik lapon a fenti linkre kattintva megnyitni az oldalt és azonnal ki is próbálgatni a weboldal funkcióit. Amikor először megnyitod az oldalt, akkor a következő kép tárul eléd:

A sokaság átlaga és szórása a csúszkákkal és az adatbeviteli mezőbe begépelve is változtatható. Például, ha megváltoztatom a sokaság átlagát 40-re, a szórását pedig 10-re, akkor ezt kapom:
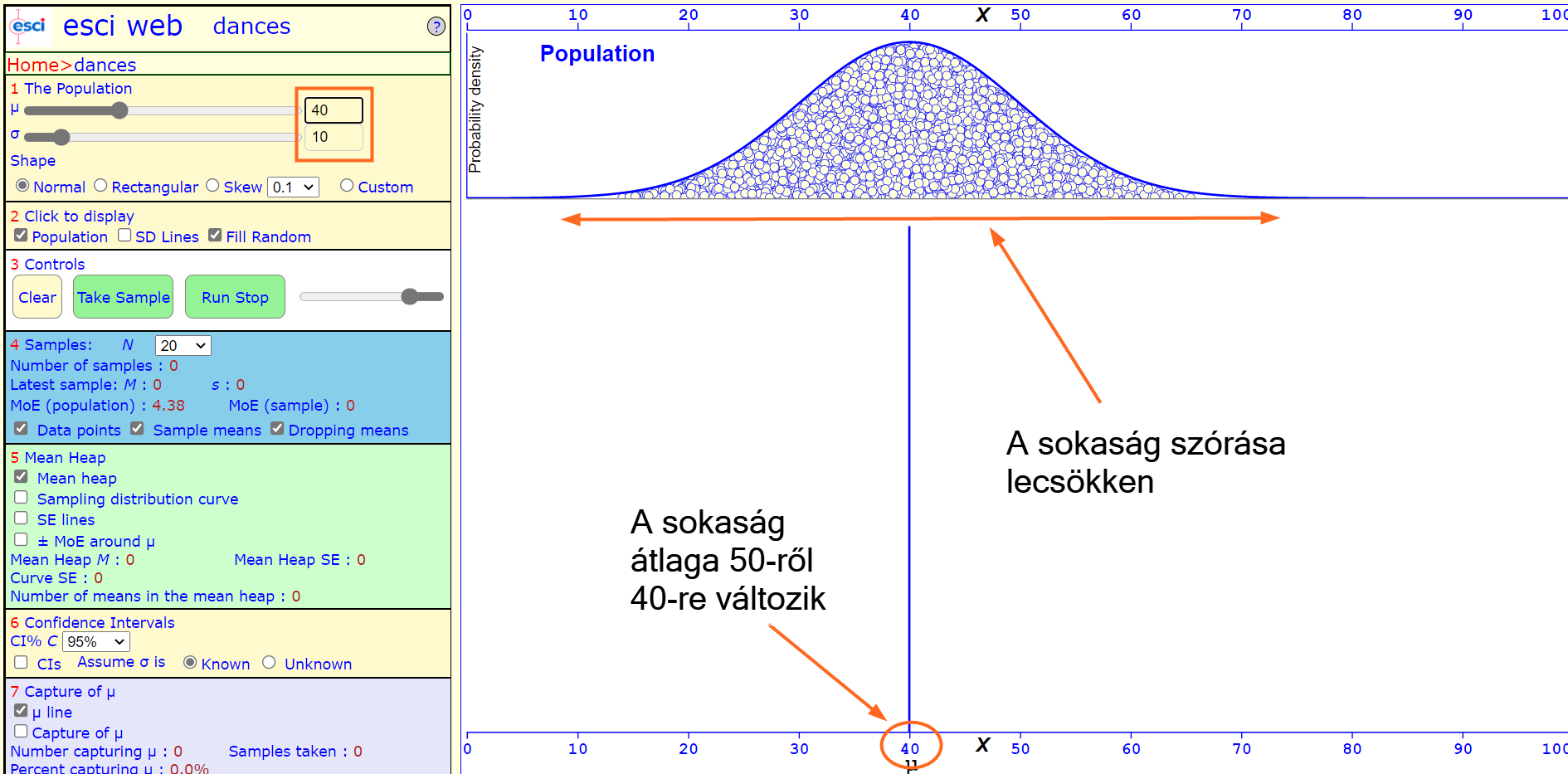
A sokaság eloszlása is változtatható, lehet egyenletes...
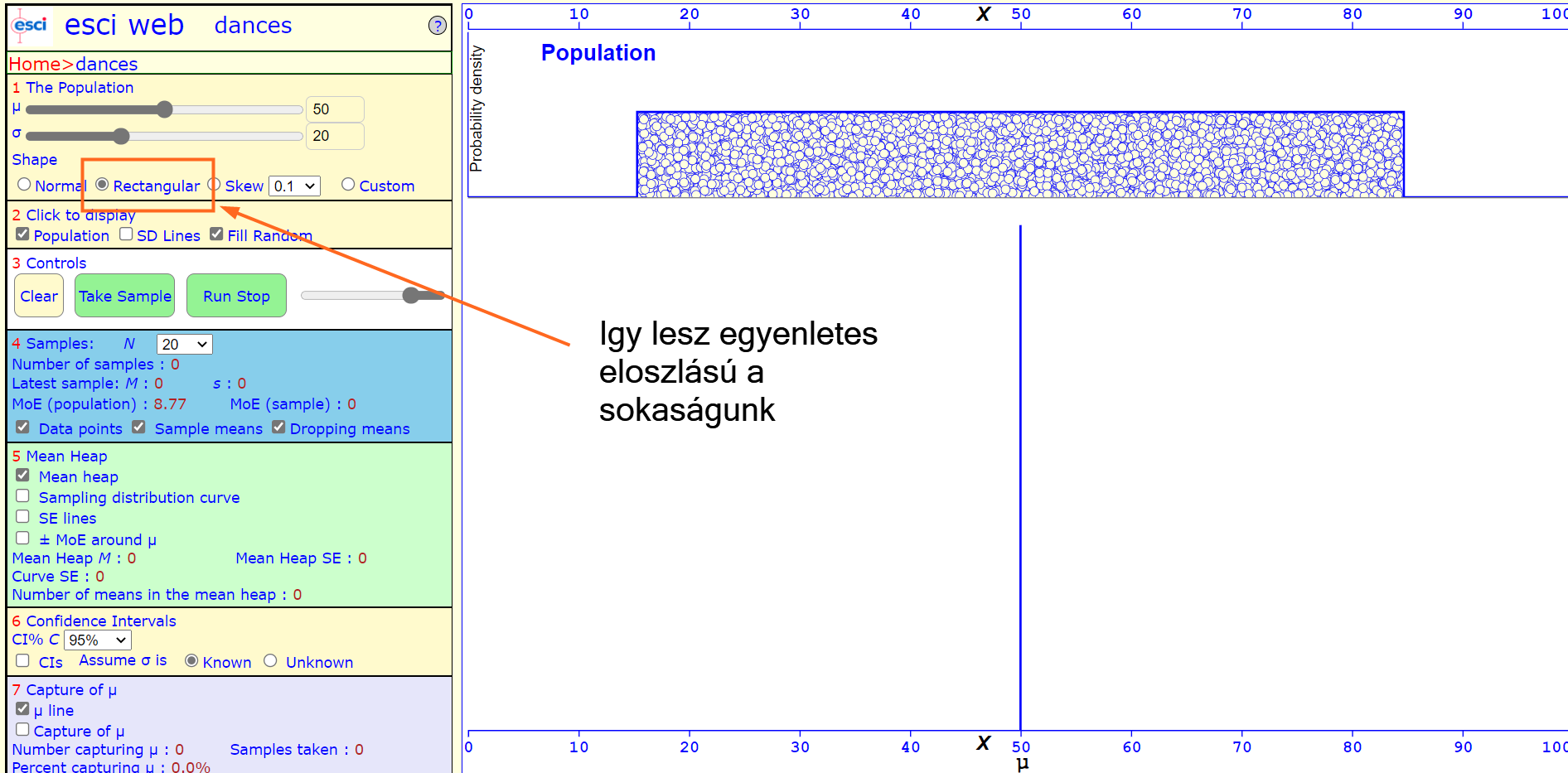
... jobbra vagy balra dölt.

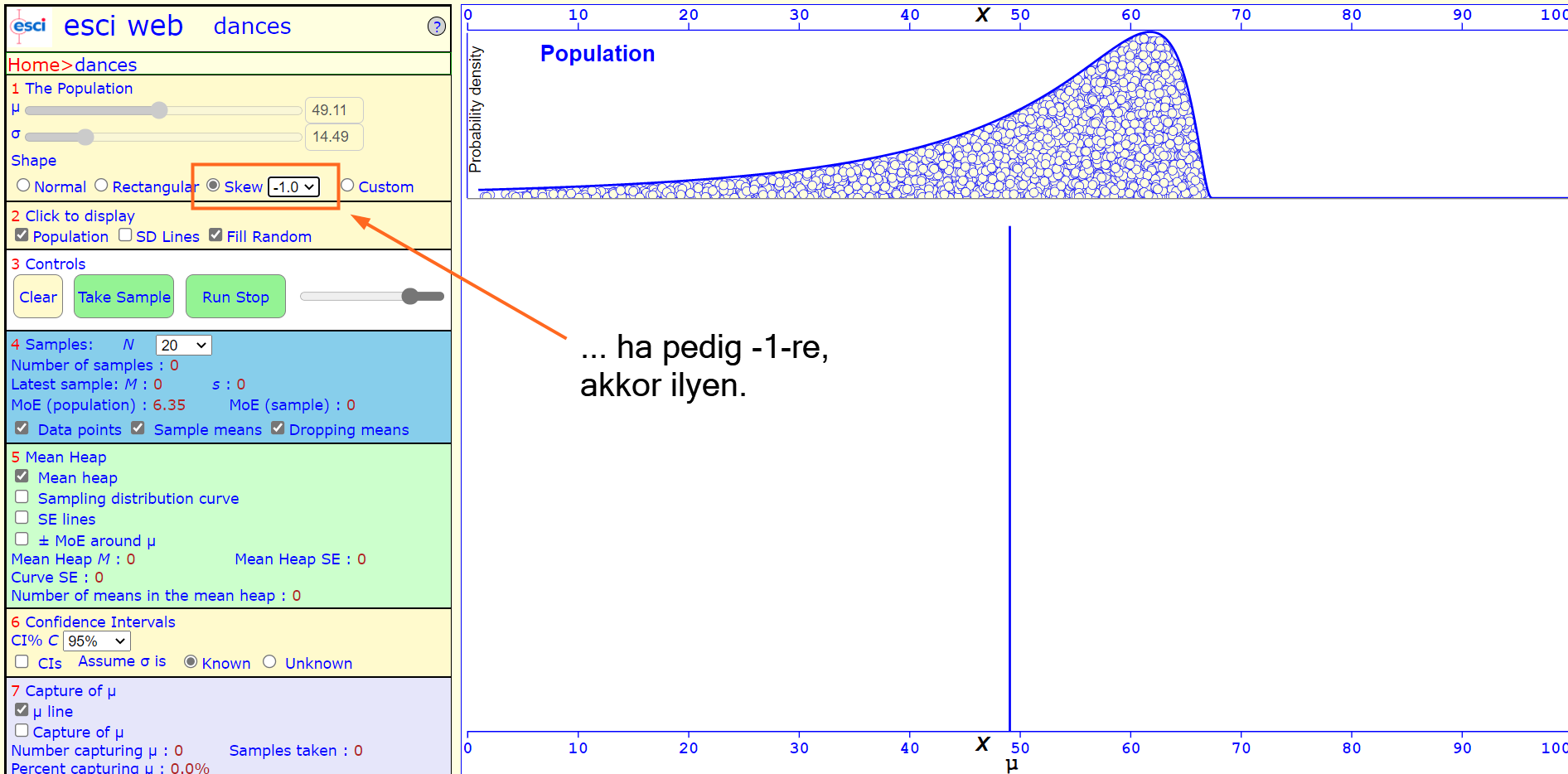
Ha egyedi eloszlásfüggvényt szeretnék megadni a sokaságomnak, akkor sajnos nem mutat semmit a munkaterületen, és nem is ajánl fel semmit, hogy hol lehetne beállítani egy egyedi eloszlásfüggvényt.

A következő szekcióban be tudod állítani, hogy látszódjon-e a sokaság, fel legyen-e töltve véletlen elemekkel, illetve berajzolja-e az 1x, 2x és 3x szórástartományokat.



És most következik az első érdekesebb rész. A "Controls" szekcióban tudod létrehozni és / vagy animálni a mintákat. A "Clear" gombbal értelemszerűen le tudsz takarítani mindent a munkaterületről. A "Take Sample" gombbal vehetsz egy mintát a sokaságból. A "Run Stop" gombbal pedig folyamatosan veheted a mintákat a sokaságból. A jobb oldalon lévő csúszkával a mintavétel animációjának sebességét tudod lassítani vagy gyorsítani.
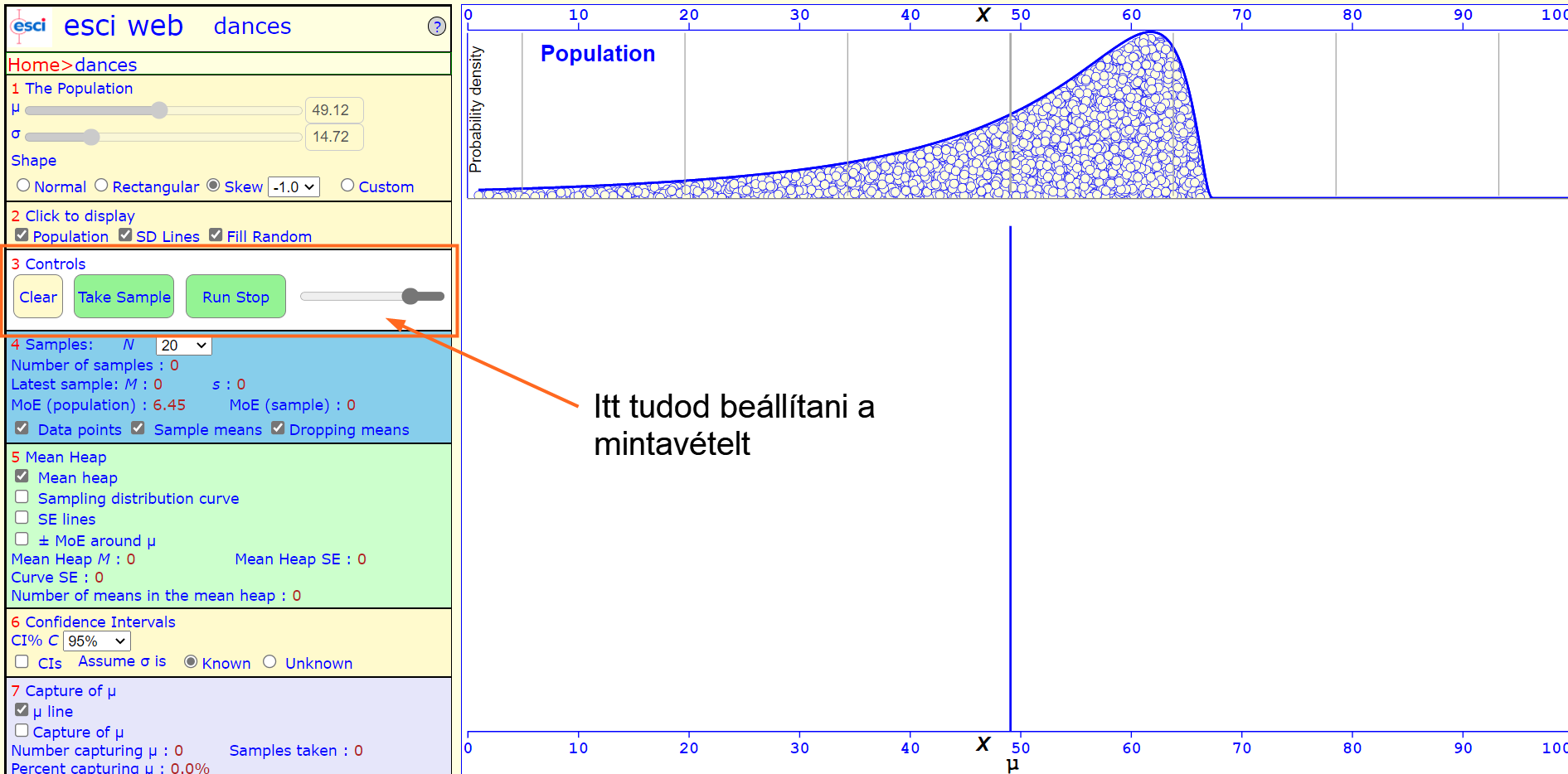
A következő szekcióban a sokaságból kivett minták tulajdonságait tudod beállítani.

Az egyik legfontosabb a minta elemszámának a beállítása.
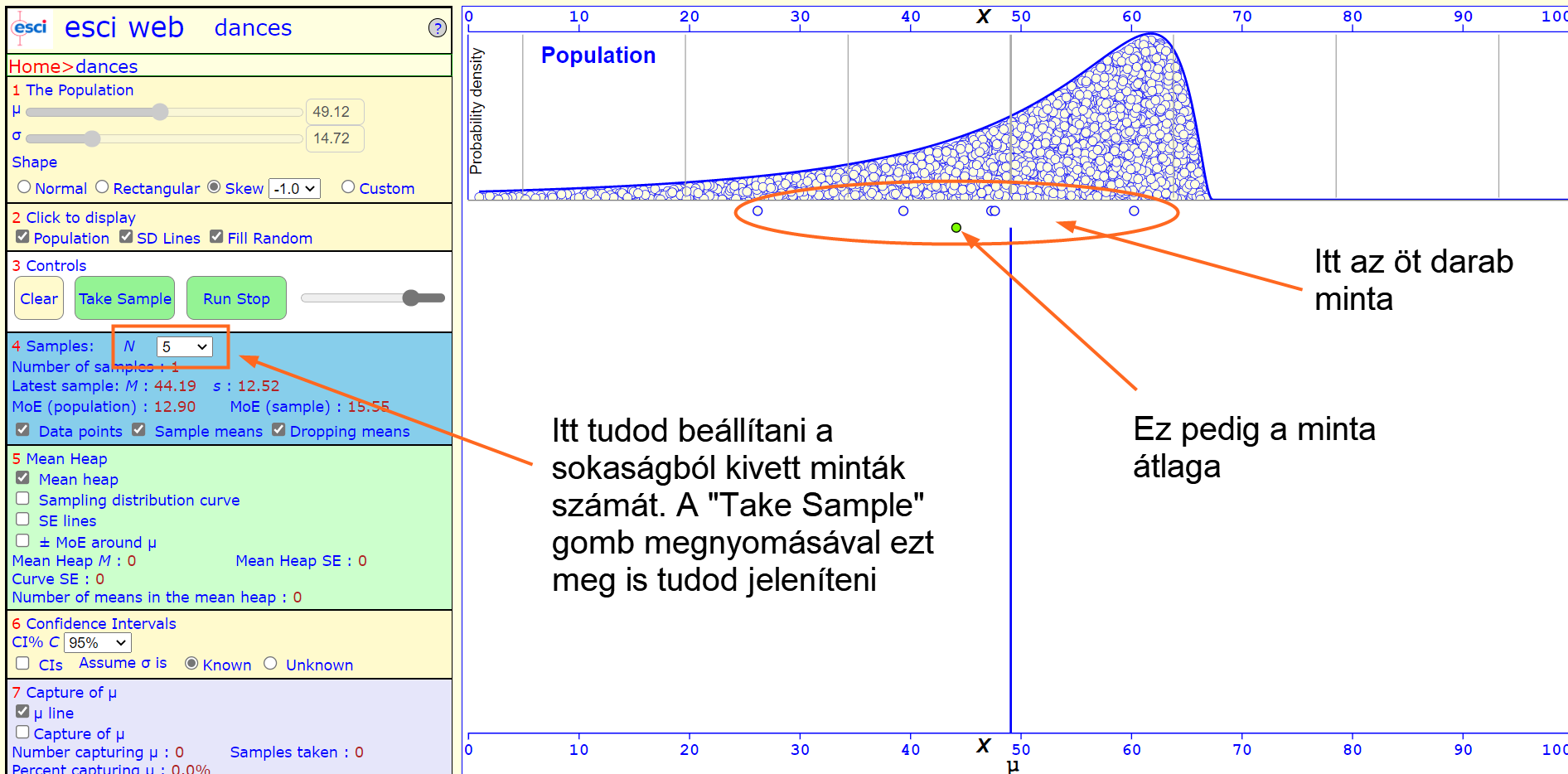
A mintaelemszám beállítása alatt a minták néhány tulajdonsága jelenik meg. A "Number of samples" értelemszerűen a sokaságból kivett minták számát jelenti, a "Latest sample" az utolsó minta átlagát és szórását jelöli (M és s). Az MoE a "Margin of Error" kifejezés rövidítése, amely tulajdonképpen a 95%-os megbízhatósági intervallumnak egy másik neve. Itt feltünteti a sokaság és az utoljára kivett minta megbízhatósági tartományát is, hogy össze lehessen hasonlítani őket.

A szekció alján újra azt lehet beállítani, hogy mi jelenjen meg.

Az ötödik szekcióban a lefelé potyogó átlagok kazalba gyűjtését lehet beállítani.
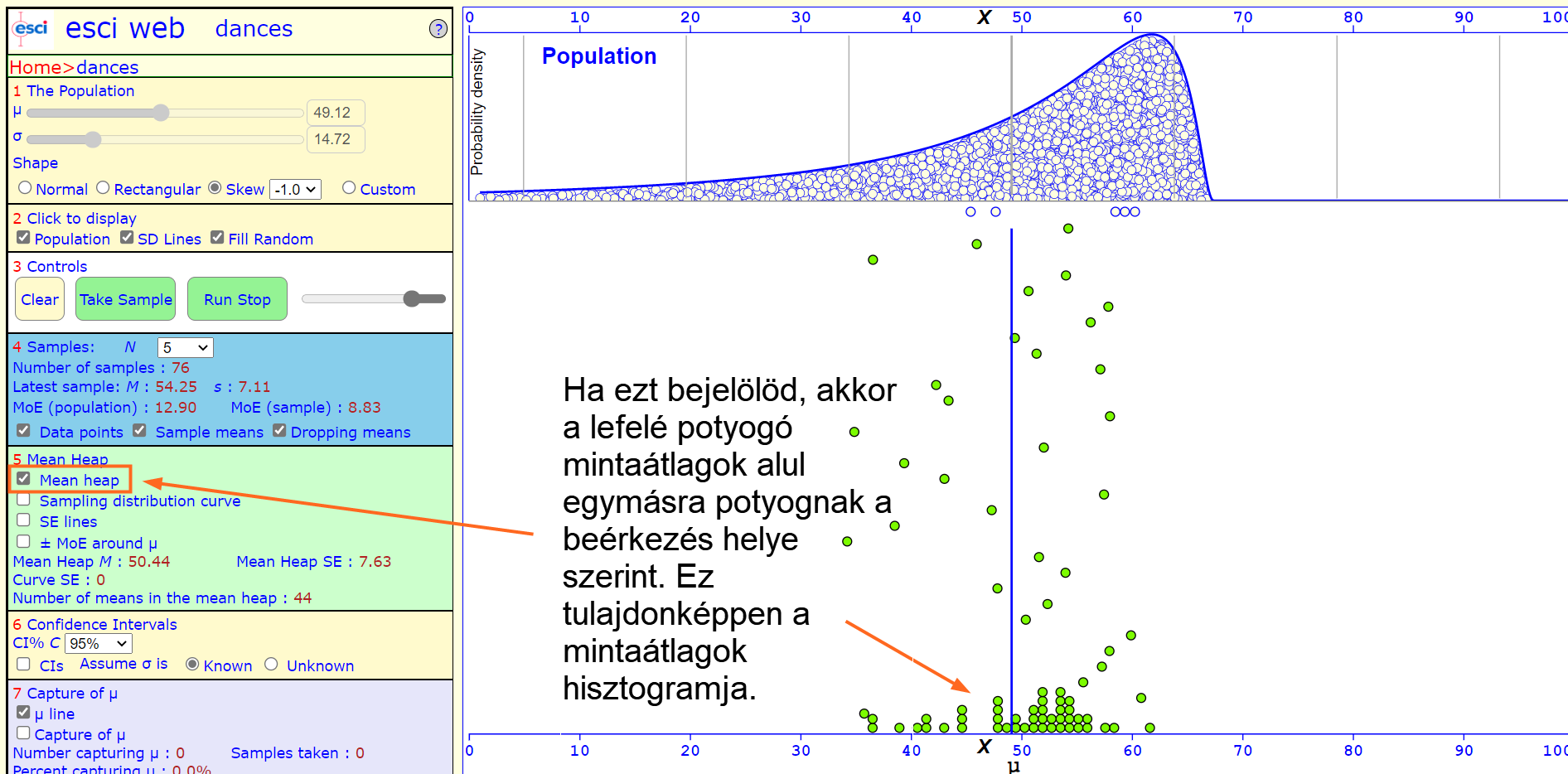
Ha a "Sampling distribution curve"-öt is bejelölöd, akkor oda fogja rajzolni az átlagok eloszlásához leginkább illeszkedő minta eloszlás görbét.

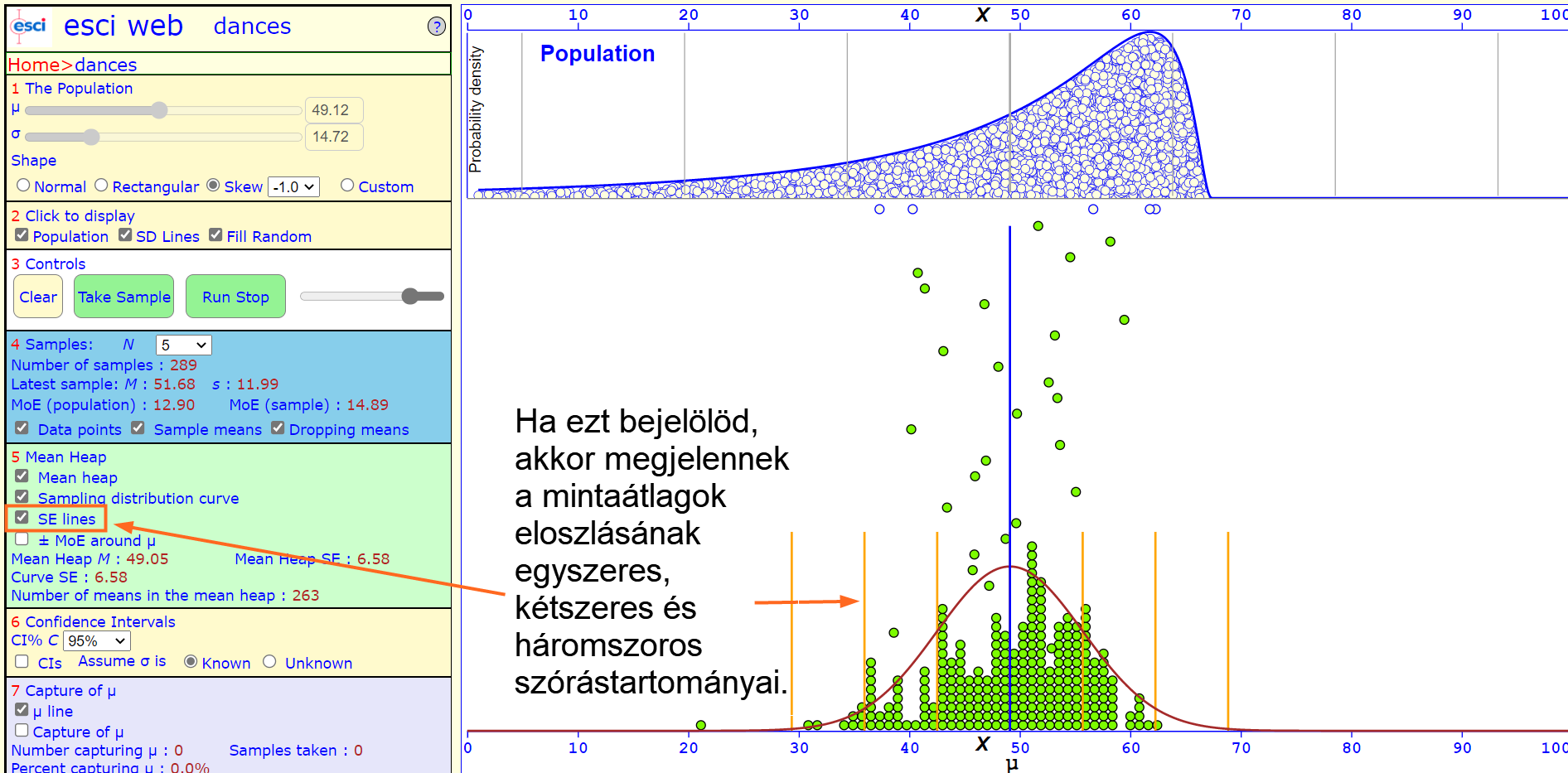
Az "SE lines" a mintaátlagok eloszlásának ±1, ±2 és ±3-szoros szórástartományát fogja bejelölni.
Ha bejelölöd a "± MoE around μ"-t, akkor pedig az a tartomány fog megjelenni, ahová a mintaátlagok 95%-a esni fog.
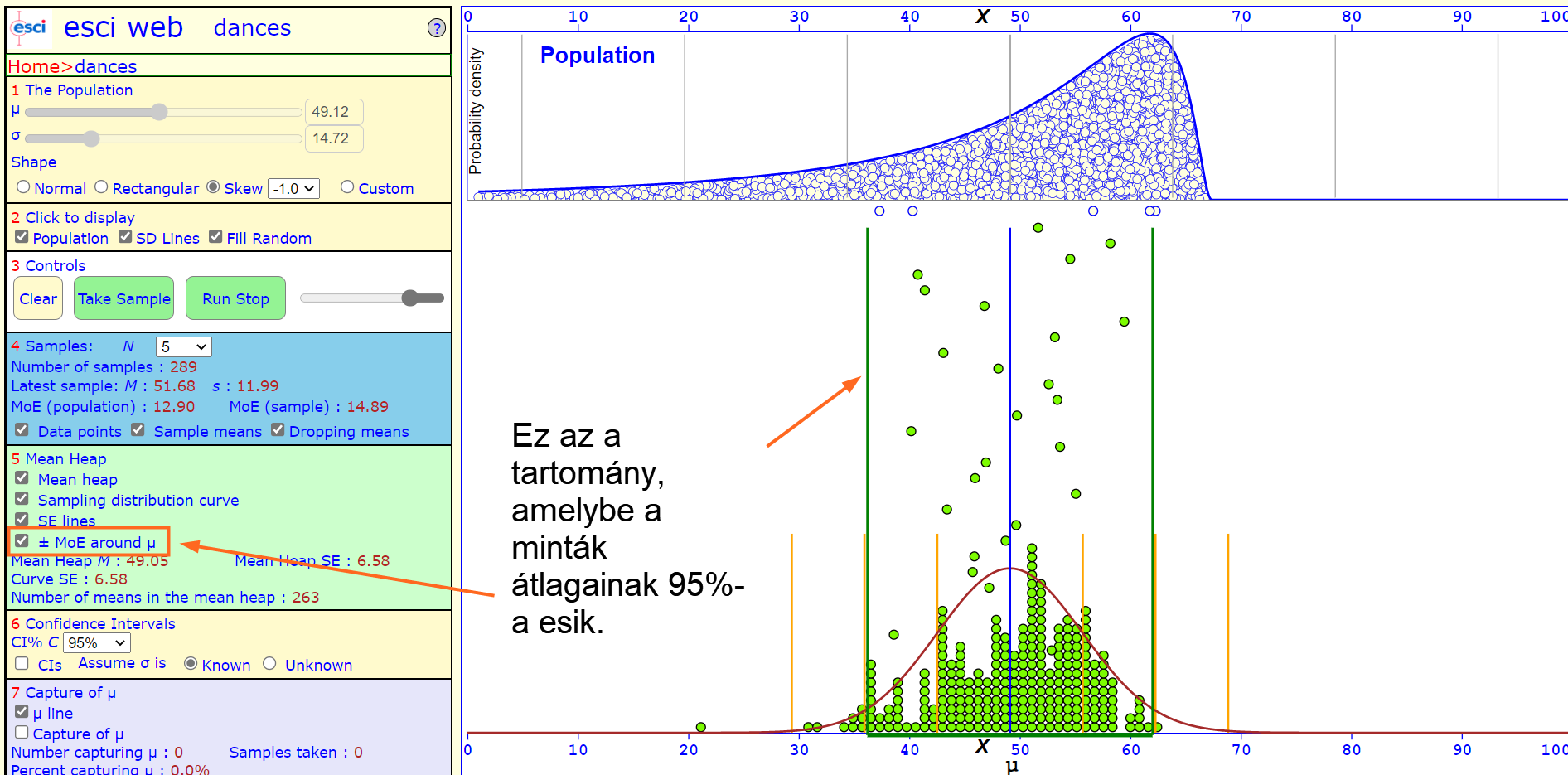
Ezek alatt a mintaátlagok eloszlására vonatkozó néhány mérőszám jelenik meg. A "Mean heap M" a mintaátlagok átlaga, "Mean Heap SE" a mintaátlagok szórása, a "Number of means in the mean heap" pedig a kazalban lévő mintaátlagok számát jelöli.

A következő részben tudod beállítani a megbízhatósági szintet, vagyis azt, hogy mennyire akarsz biztos lenni a döntésed helyességében.

Ha CIs-t kipipálod, akkor a minták átlagainál megjelennek a mintaátlagokhoz tartozó megbízhatósági intervallumok, amelyeket a program az átlag standard hibája (Az átlag standard hibája) alapján számít ki.
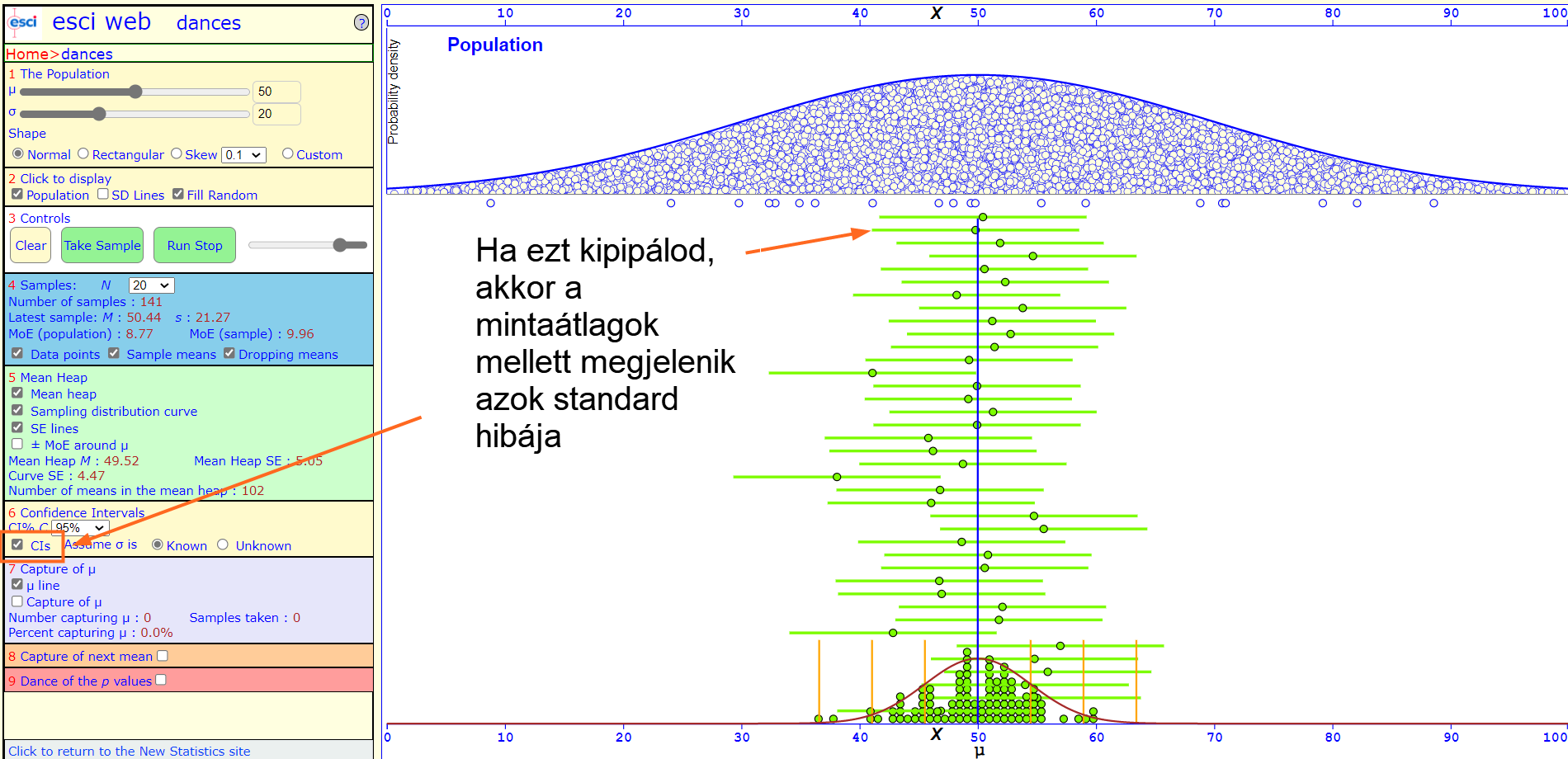
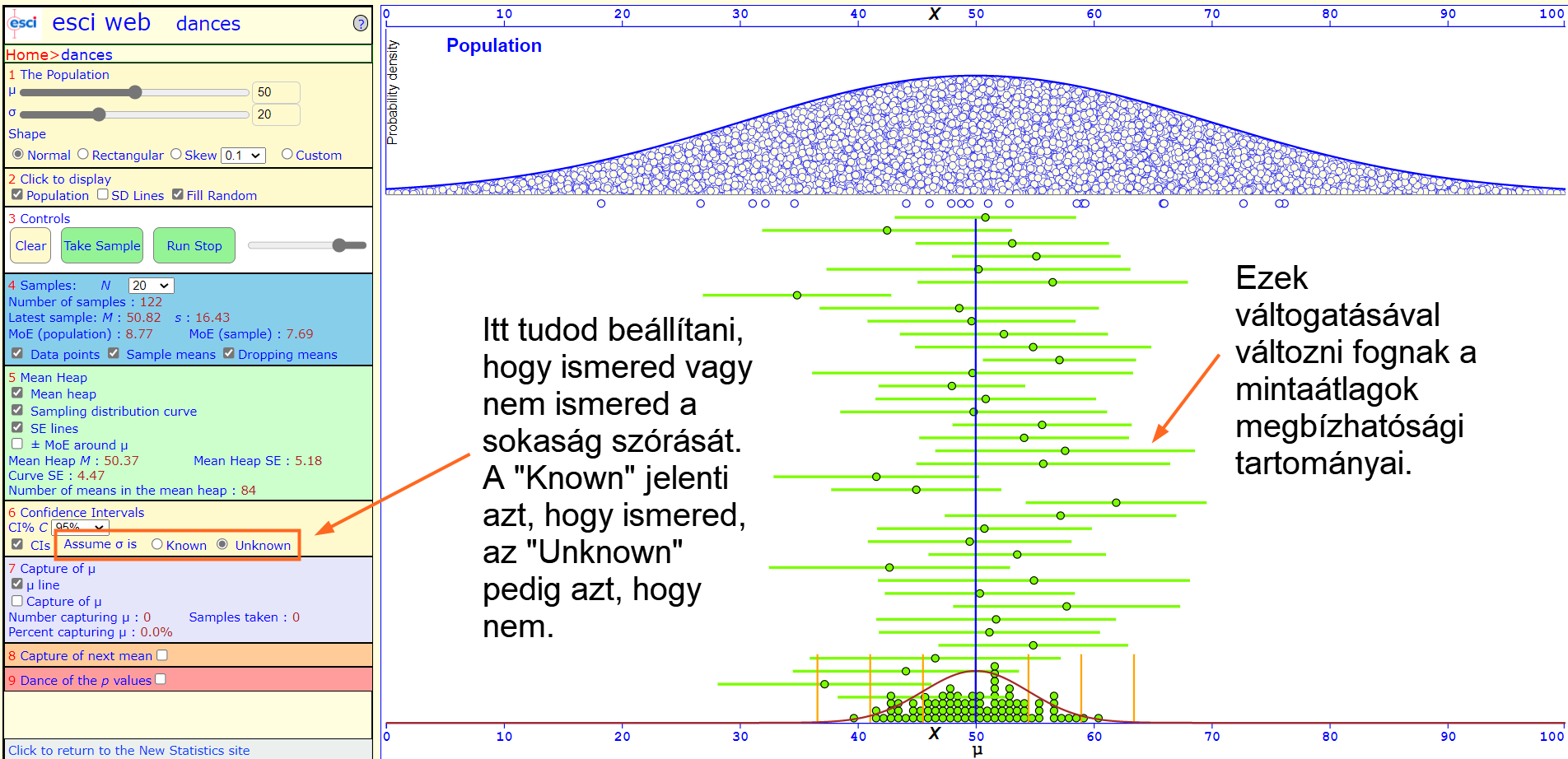
Az is praktikusan kiválasztható, hogy vajon ismerjük-e a sokaság átlagát, vagy sem. Ha ismerjük, akkor a program a sokaság szórása alapján számítja ki a mintaátlagok standard hibáját, ha pedig nem, akkor a sokaság szórását a minták szórásával helyettesíti (Adathalmazok elemeinek szóródása - A szórás és a variancia). A rádiógombok váltogatásával láthatod, hogyan változnak a mintaátlagok megbízhatósági tartományai. A megbízhatósági szint változtatásával pedig a mintaátlagok megbízhatósági tartományainak szélessége fog változni.
Összefoglalás:
Ebben a cikkben egy remek vizualizációs eszközt mutattam be, amely véleményem szerint jól használható az oktatásban arra, hogy bemutassuk vele a sokaság és a minta kapcsolatát, illetve megvilágítsuk azt, hogy milyen korlátai vannak annak, ha egy mintából próbálunk következtetni a sokaság tulajdonságaira. A minták animációja látványosan mutatja be, hogy mennyire biztos vagy bizonytalan egy minta alapján bármit is állítani a sokaságról, például remekül be lehet mutatni, hogy a mintaszám csökkentése vagy növelése mennyire lesz hatással a döntésünk megbízhatóságára.
Most csak az oldal használatát mutattam be, de a következő cikkekben bemutatom majd azt is, hogy milyen következtetéseket lehet látványosan bemutatni az oldal alkalmazásával.
Források:
Geoff Cumming & Robert Calin-Jageman: Introduction to the new statistics: Estimation, Open Science, and Beyond, Routledge Subs. of International Thomson Org. 29 West 35th Sreet New York, NYUnited States, October 2016
ISBN:978-1-138-82552-9
Geoff Cumming youtube-csatornája
https://www.youtube.com/channel/UCwRbwVb6mRKuyXtV1td-vig





