A brazíliai esőerdők pusztulása előtérbe helyezte az éghajlatváltozással kapcsolatos témákat. Kis túlzással szinte a csapból is ez folyik. Több írást is olvastam arról, hogy mennyire változik az időjárás, hogy egyre szélsőségesebbek az időjárási jelenségek. Igazából kíváncsi voltam arra, hogy vajon mennyire igaz ez Magyarország esetében. Nem gondoltam teljesen átfogó éghajlati elemzést készíteni, inkább csak benyomásokat szeretnék szerezni olyan dolgokról, amit saját tapasztalataim alapján érzékelek. Például úgy érzem, hogy nyáron egyre magasabbak a napi csúcshőmérsékletek, egyre több a kánikula. Vajon ez most csak amiatt van így, mert öregszem és rosszul bírom a meleget, vagy pedig tényleg melegebbek a nyarak most, mint 30-40 évvel ezelőtt.

Hangsúlyozom, hogy most nem idősorok elemzését szeretném elkészíteni és nem trendeket szeretnék elemezni, csak annyit akarok, hogy összehasonlítsam a jelenlegi hőmérsékleti adatokat a múlttal, hogy vajon kimutatható-e valamilyen szignifikáns különbség a kettő között.

Természetesen el is kezdtem keresgélni és szerencsére találtam olyan adatbázisokat, amelyek történelmi adatokat is tartalmaznak, ezeket remekül fel lehet használni egy ilyen elemzés elkészítésére. Az egyik praktikus hely, ahol ilyen történelmi adatsorok is megtalálhatók, az Országos Meteorológiai Szolgálat weboldala, ahol – bár kissé eldugva – egészen komoly adatsorok elérhetők.

http://owww.met.hu/eghajlat/eghajlati_adatsorok/bp/Navig/202.htm

Innen töltöttem le először is az átlaghőmérséklettel kapcsolatos havi adatokat az 1901 és 2000 közötti időszakról. Az adatok szépen táblázatba vannak rendelve és az egyes oszlopnevek jelentése is megtalálható egy leírásban ugyanitt

http://owww.met.hu/eghajlat/eghajlati_adatsorok/bp/Navig/104.htm.

Az adatokat viszont először a vágólapon keresztül egy egyszerű szövegfile-ba kellett bemásolnom, hogy azt utána használható formában tudjam beolvasni egy táblázatkezelő programba. Ezt úgy tettem meg, hogy létrehoztam a munkamappában egy egyszerű szövegfile-t (jobb egérgomb – ’Új’ – ’Szöveges dokumentum’ – filenév megadása), majd CTRL-C-vel kimásoltam az adatokat a weboldalról és CTRL-V-vel bemásoltam a szövegfile-ba. Sajnos ennek az adatfile-nak nem találtam meg a konkrét folytatását, a met.hu-n, de más formában megtalálhatók az adatok, de csak 2009-től mostanáig (legalábbis én nem találtam meg a többit).

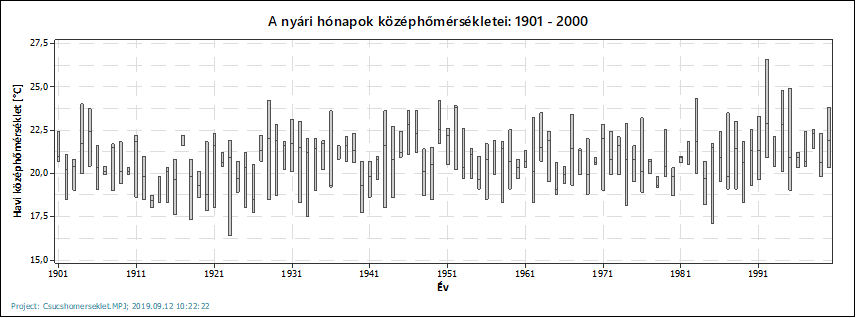
Amikor megvoltak az adatok, akkor elkezdtem elemezni őket, először elkészítettem a sokaságnak szánt adatsor elemzését. Először készítettem egy boxplot diagramot a havi adatokról éves bontásban, azaz minden 12 hónap adata megad egy adatcsoportot, amelyet utána ábrázolni lehet. Így néznek ki az egyes hónapokban tapasztalt hőmérsékletek átlagai 1901 és 2000 között.

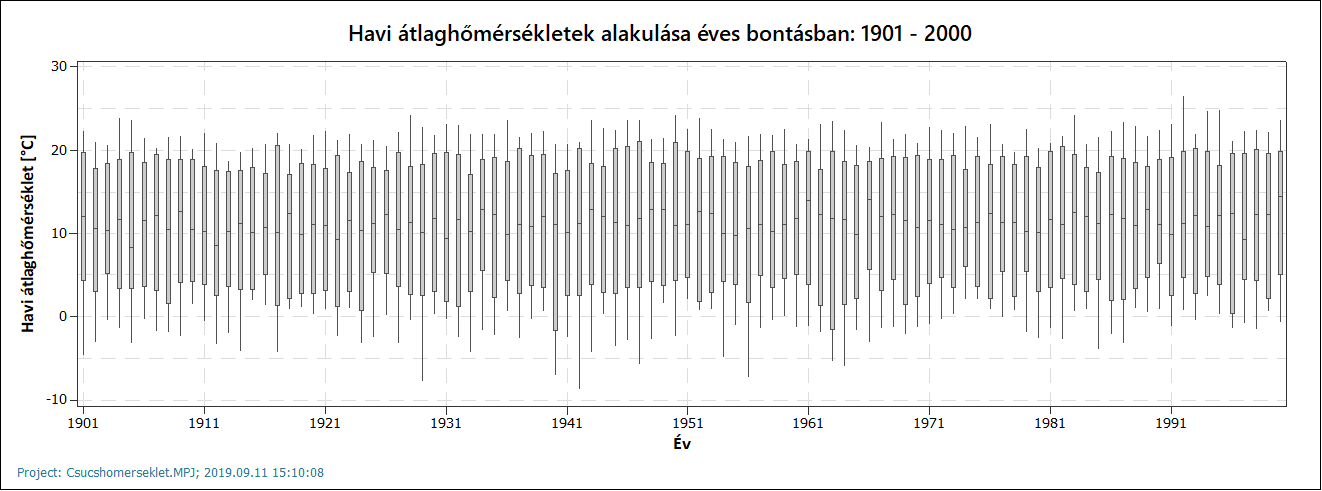
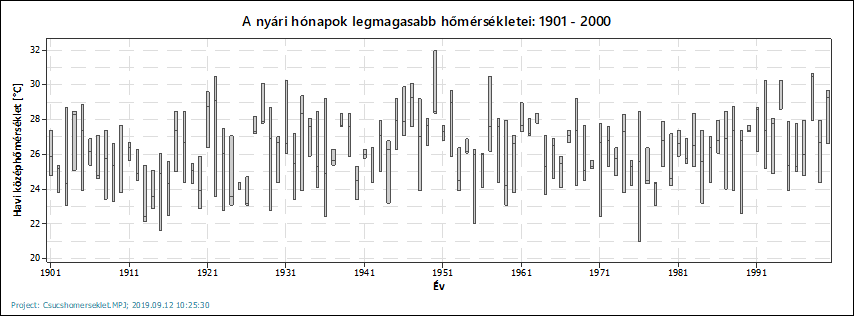
Most nézzük meg ugyanezt a havi csúcshőmérsékletekre.

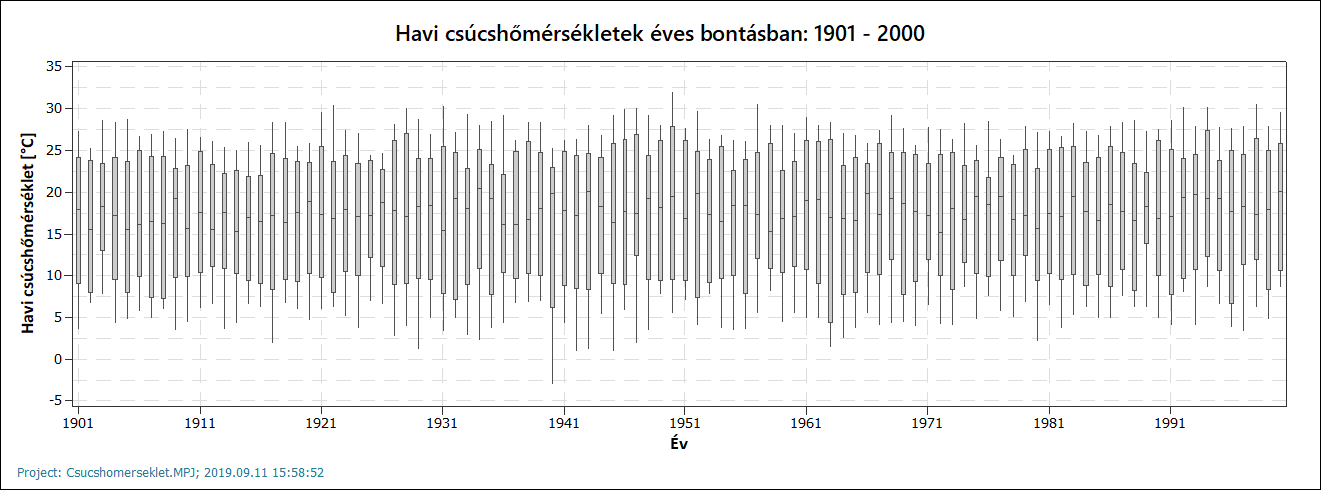
A két diagramról jól látható, hogy a 20. században a havi átlaghőmérsékletek és csúcshőmérsékletek nemigen változtak, ránézésre mindkét adatsor stabil értékeket mutat. Az éven belüli adatok esetében nincsenek kiugróan alacsony vagy magas értékek (amelyek *-gal lennének jelölve a „dobozok” alatt vagy felett). Noha egyik adatsor sem normál eloszlású, hosszútávú történeti adatokról beszélhetünk, ezért sokaságként tekinthetünk rájuk.

Mivel a Khí-négyzet próba erősen kívánja, hogy az adatok normál eloszlásúak legyenek, ezért mindkét sokaságra elindítottam egy normalitás vizsgálatot. Sajnos mindkét esetben azt kaptam, hogy az adatok nem normál eloszlásúak. De vajon miért?

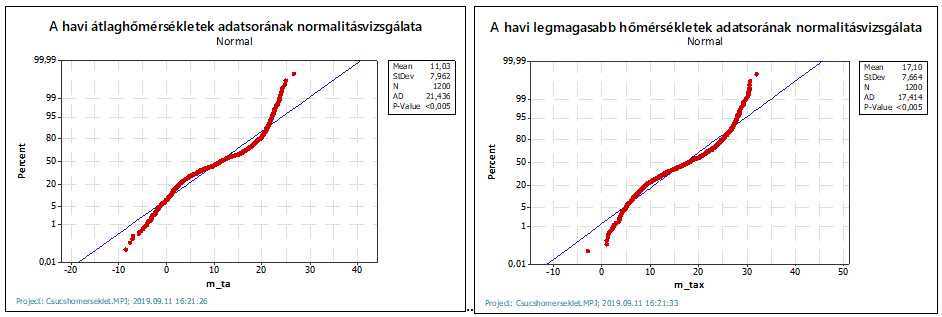
Hossza Rövid gondolkodási idő után rájöttem, hogy az adatsorok egyaránt tartalmazzák a tavaszi, nyári, őszi és téli hónapok adatait is, vagyis több különböző körülmények között született adatsort is tartalmaznak, azaz a kevert adatok simán okozhatják a normál eloszlástól eltérő viselkedést. Az alábbi hisztogramon is látható, hogy az adatok gyakoriságai egy több csúccsal rendelkező eloszlásképet mutatnak.

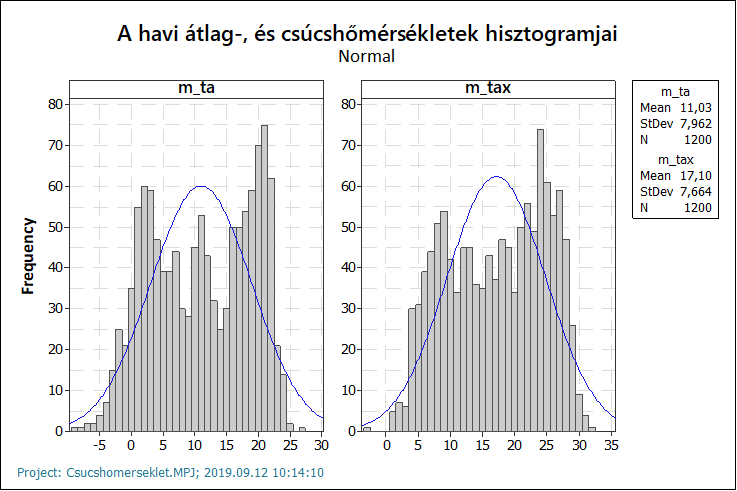
Mivel engem igazából csak a nyári magas hőmérsékletek érdekelnek, ezért kiszűrtem minden év júniusi, júliusi és augusztusi adatait és csak ezeket vizsgáltam meg.

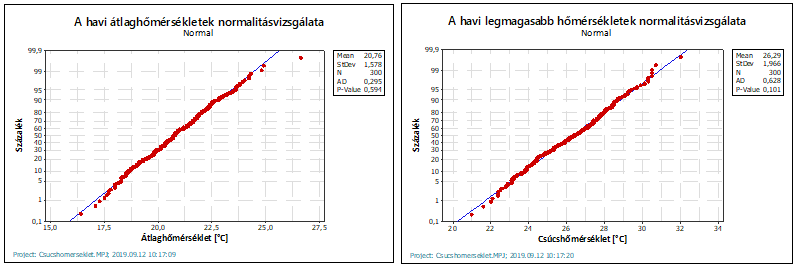
Az így megszűrt adatok már normál eloszlásúak (a P-value értékek mindkét esetben nagyobbak, mint 0,05), így már alkalmasak a szükséges hipotézis vizsgálatok elvégzésére.

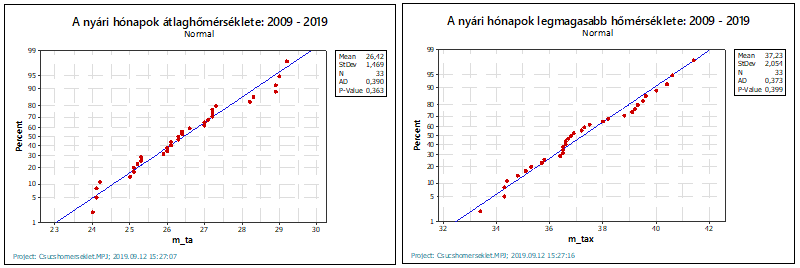
Természetesen ellenőriztem a mintaként használt 2009 és 2019 közötti eredmények eloszlását is, szerencsére ezek is normál eloszlásúak.

De mielőtt ezekbe belefognék, kiegészítettem a sokaságok adatsorait a 2009 és 2019 közötti nyári hónapok adataival és az így kapott adatsorokat a korábbiakhoz hasonló boxplot-diagramon ábrázoltam.

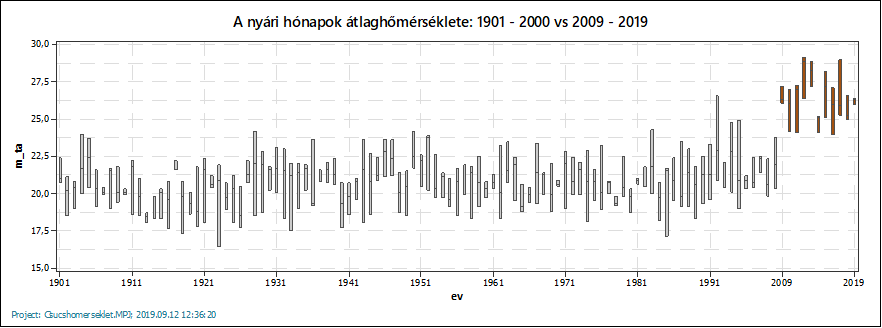
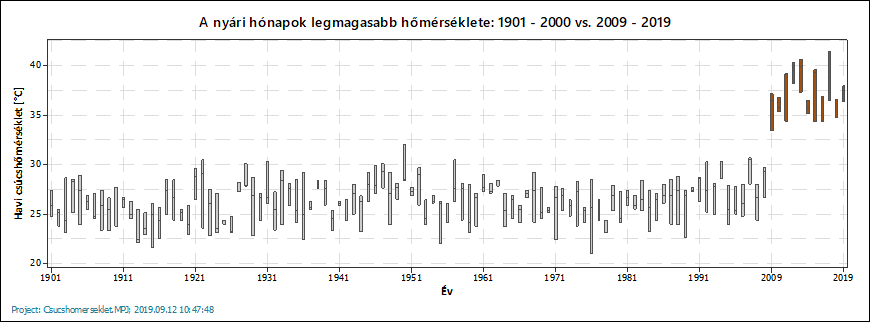
Mondjuk ezzel most lelőttem a poént, hiszen már a grafikonokon is szembeötlő a különbség a történeti adatok és a jelenleg tapasztalt hőmérsékletek között. Az egyetlen dolog, amit sajnálok, hogy a 2000 és a 2009 közötti nyarak adatait nem találtam meg, így nem teljesen tiszta, hogy igazából mi történt azalatt a 8 év alatt, amitől ekkorát változott az átlag-, és a csúcshőmérséklet. Sajnos nem lehet teljesen kizárni azt, hogy a két adatsor közti különbséget, vagy annak egy részét az adatok forrásai közötti különbség is okozhatta. De ez igazából mindegy is, hiszen most nem célom tudományos következtetések levonása, csak egy statisztikai elemző eszköz bemutatása.

Noha teljesen egyértelműnek tűnik a XX. századi és a jelenlegi hőmérsékletek közötti különbség, azért a rend kedvéért készítettem egy egymintás Z-próbát (Z, mint Z-próba – egymintás). Mielőtt ezt megtettem, készítettem egy leíró statisztikát a két sokaságra, hogy meglegyen a sokaságok átlaga és szórása. Ez alapján az átlaghőmérsékletek sokaságának átlaga 20,763 °C, szórása pedig 1,578 °C. A legmagasabb hőmérsékletek átlaga 26,289 °C, szórása pedig 1,966 °C.

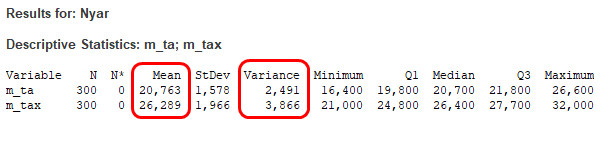
A két egymintás Z-próba egyértelműen bizonyítja, hogy a 2009 és 2019 közötti adatok nem azonosak a XX. század során mért átlaghőmérsékletekkel. A havi átlaghőmérsékletek esetében a hipotézisünk az volt, hogy a minta átlaga meg fog egyezni a sokaság átlagával, amely nem következett be, hiszen a sokaság átlaga (20,763 °C) nincs benne a minta átlagának megbízhatósági tartományában (95% CI: 25,887 °C – 26,962 °C), illetve a P-value is 0.

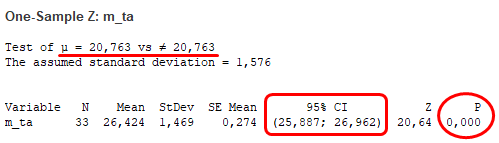
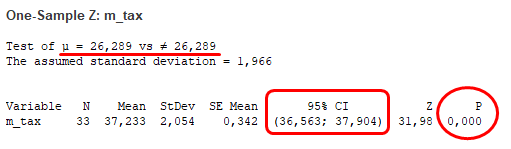
Hasonlóan a havi csúcshőmérsékletek esetében is hasonló a helyzet, a minta átlagának megbízhatósági tartományában (95% CI: 36,563 °C – 37,904 °C) semmiképpen sem lehet benne a sokaság átlaga (26,289 °C). A P-value ez esetben is 0.

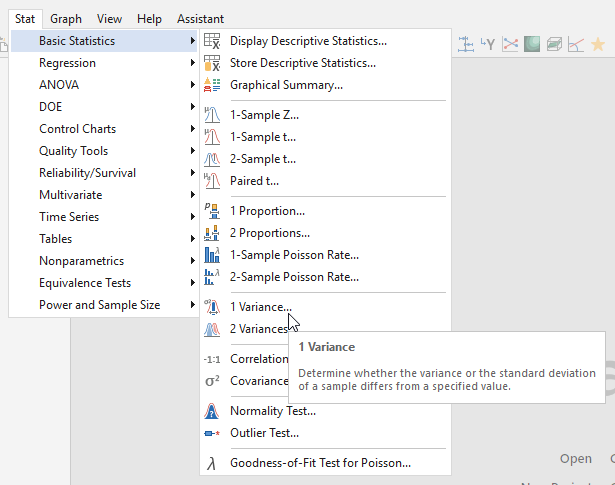
De vajon a hőmérsékletek szóródása nagyobb lett-e? Mondhatjuk-e, hogy a hőmérsékletek ingadozása lényegesen megnőtt a múlt század óta? Ehhez fogom használni a 1-variance tesztet. A 1-variance teszt a Minitab-ban a következő helyen található:

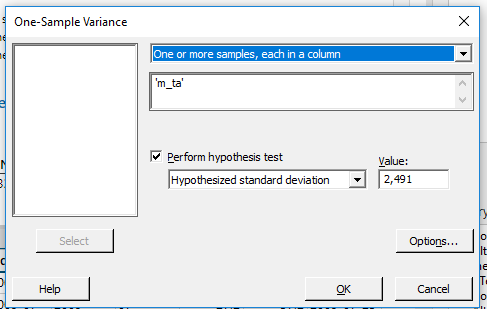
Az ezután megjelenő párbeszéd panelen csak annyi dolgunk van, hogy kiválasszuk a vizsgálandó paramétert.

Az 'Options' gomb megnyomásával be lehet állítani a megbízhatósági szintet, illetve a hipotézis teszt típusát. Alapból 95%-os megbízhatósági szint és kétoldalas hipotézis vizsgálat van beállítva, ezen most nem akarunk változtatni. Eredményként a következőket kaptuk.

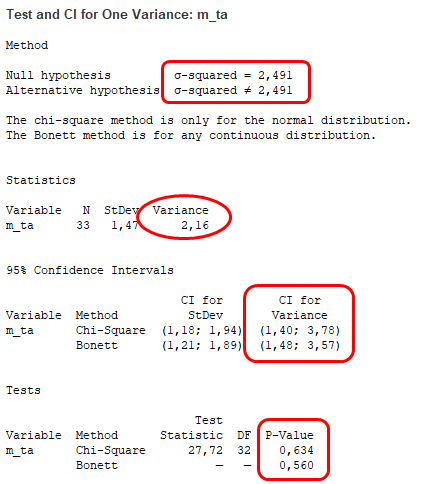
A teszt elején szokásosan megadja a Minitab, hogy mi a nullhipotézis és az alternatív hipotézis. Ezután figyelmeztet minket a program, hogy a khí-négyzet módszer csak akkor használható, ha az adatok normál eloszlásúak és minden egyéb folytonos eloszlás esetén a Bonett-teszt eredményeit kell figyelembe venni. Na, ez külön megérne egy misét, mert ez a Bonett-teszt nem igazán ismert, igazán értelmes magyarázatát még nem találtam meg sehol. Maradjunk annyiban, hogy kövessük a Minitab ajánlását és ha az adatsorunk nem normál eloszlású, akkor a Bonett teszt eredményeit vegyük figyelembe. A ’Statistics’ pont alatt nem sok dolog történik, a Minitab kiírja a teszthez használt adatsor elemszámát, szórását és varianciáját. Ezután meghatározta a megbízhatósági tartományokat a khí-négyzet és a Bonett tesztek alkalmazásával. Jól látszik, hogy nincs lényeges különbség a két teszt eredményei között. Végül meghatározta a tesztekhez tartozó P-értékeket is. Mivel mindkettő nagyobb, mint a teszt elején választott 95%-os megbízhatósági kritérium által megadott 0,05, ezért a nullhipotézist nem tudjuk elvetni.

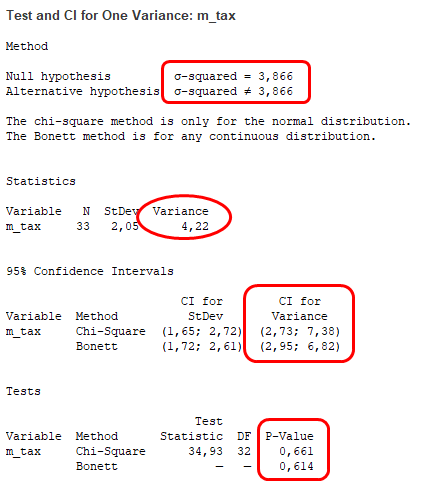
A csúcshőmérséklet esetében hasonló a helyzet, itt sem lehet egyértelműen elvetni a nullhipotézist.

Következtetés: A tesztek alapján egyértelműen ki tudjuk jelenteni, hogy a történeti adatokhoz képest jelentősen emelkedtek a nyári hőmérsékletek, de azt nem tudjuk igazolni, hogy a nyári hőmérsékletek szóródása lényegesen növekedett volna a korábbiakhoz képest, vagyis a nyári hőmérsékletek esetében nem igazolható a hőmérsékletingadozások növekedése. Természetesen megérne egy misét a téli átlag-, és legalacsonyabb hőmérsékletek vizsgálatai is, de ezeket most nem végzem el, legyenek ezek házi feladatok az érdeklődő olvasók részére.