
Erre a kérdésre Francis Galton, a 19. század egyik legtehetségesebb matematikusa, mellesleg Charles Darwin unokaöccse kereste a választ. Sok már kutatása mellett az egyik kérdés, ami foglalkoztatta az volt, hogy hogyan öröklődnek az emberek egyes tulajdonságai a szülőkről a gyerekekre.
Az egyik terve az volt, hogy összegyűjti szülők testmagasság adatait, majd a gyerekeikét és összehasonlítja őket. Sajnos az adatok összegyűjtése nagyon lassan haladt, ezért híres unokabátyja azt tanácsolta neki, hogy kísérleteit inkább a borsókavirág (bükköny) magvaival próbálja meg, mert így sokkal gyorsabban célt ér. Galton hallgatott unokafivére tanácsára és egy csomó magot nagyság szerint csoportosított, majd elültette őket. A magokból kikelt növények magvait csoportoként összegyűjtötte és megmérte őket. Eredményül a következőket kapta.

A kapott adatok alapján Galton arra a következtetésre jutott, hogy ha a szülői egységek egy egységnyivel nagyobbak, akkor az utódmagvak csak harmadannyival nagyobbak. Ebből a tényből Galton a következő általánosabb következtetésre jutott, amelyet 1877-ben fejtett ki egy előadásában:
A visszatérés (reversion) az a tendencia, amely az ideális átlagos utódtípust a szülői típustól elválasztja, hogy visszatérítse ahhoz, amit durván, de alighanem találóan az átlagos elődtípusként írhatunk le. Ha csakis a családi változékonyság volna az egyszerű leszármazás során az egyetlen olyan folyamat, amely befolyásolja a minta jellegzetességeit, akkor egy faj ideális átlagtípusától való szóródás a végtelenségig növekedhetne a nemzedékek egymásutánjával, ámde a visszatérés (reversion) ellenőrzés alatt tartja a növekedést és nyugvópontra juttatja.
Tehát ha a 170 cm magas szülők gyerekei között kell lennie 180 cm körülinek is, majd e gyermek gyermekei közt már 190 cm körülinek is elő kell fordulnia, akkor (kellően nagy gyerekszámot feltételezve) néhány nemzedék alatt kitenyésztődtek volna óriások és törpék is.
8 évvel később sikerült összegyűjteni 205 szülőpár és gyermekeik adatait, amelyeket végül táblázatba rendezett, illetve grafikon segítségével is feldolgozott.
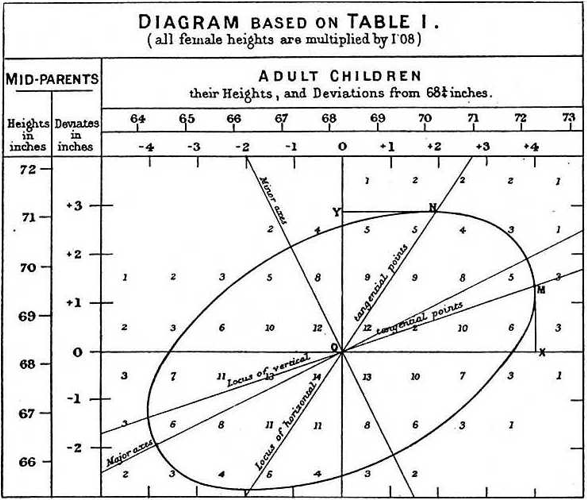
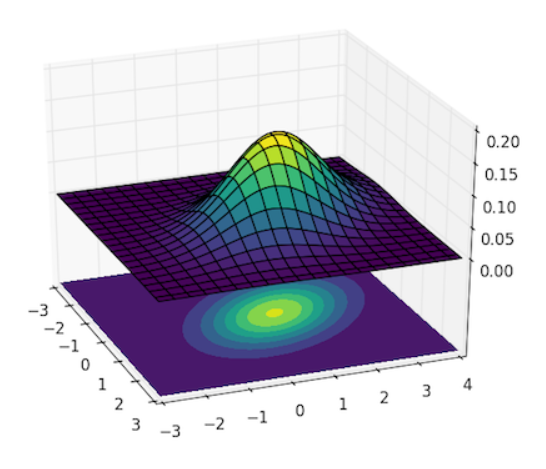
Természetesen az embereknél ugyanazt a törvényszerűséget figyelte meg, amelyet a borsókavirág magvainál. De felfedezett valami mást is. Azt vette észre, hogy a táblázatban az azonos gyakoriságokat mutató mezők egy vagy több ellipszist írnak le. Mintha ezek az ellipszisek egyfajta szintvonalai lennének egy háromdimenziós Gauss-, vagy normál-eloszlásnak, mint egy térképen.
 Ezenkívül Galton megpróbált kapcsolatot találni a szülők és a gyerekek átlagos magassága között. Ha a szülők testmagasságaihoz berajzolta a grafikonba a gyerekek testmagasságainak átlagait, akkor egy nagyjából egyenes vonatal kapott. Ha a szülők testmagassága három egységgel tért el a nagyátlagtól, akkor az utódok testmagassága csak két egységgel tért el ugyanettől. Megpróbálta ezt fordítva is, azaz a gyerekek átlagos testmagasságaihoz rajzolta be szülők testmagasságainak átlagait. Azt várta, hogy a két egyenes egybe fog esni, de nem ezt kapta. Azt látta, hogy a két egyenes egy szöget zárt be. Későbbi kutatásai során észrevette, hogy minél erősebb a korreláció a két összehasonlított mennyiség között, annál kisebb a két egyenes által bezárt szög, illetve fordítva is igaz ez, azaz minél gyengébb a korreláció, annál nagyobb a két egyenes szöge egymáshoz képest.
Ezenkívül Galton megpróbált kapcsolatot találni a szülők és a gyerekek átlagos magassága között. Ha a szülők testmagasságaihoz berajzolta a grafikonba a gyerekek testmagasságainak átlagait, akkor egy nagyjából egyenes vonatal kapott. Ha a szülők testmagassága három egységgel tért el a nagyátlagtól, akkor az utódok testmagassága csak két egységgel tért el ugyanettől. Megpróbálta ezt fordítva is, azaz a gyerekek átlagos testmagasságaihoz rajzolta be szülők testmagasságainak átlagait. Azt várta, hogy a két egyenes egybe fog esni, de nem ezt kapta. Azt látta, hogy a két egyenes egy szöget zárt be. Későbbi kutatásai során észrevette, hogy minél erősebb a korreláció a két összehasonlított mennyiség között, annál kisebb a két egyenes által bezárt szög, illetve fordítva is igaz ez, azaz minél gyengébb a korreláció, annál nagyobb a két egyenes szöge egymáshoz képest.

Galton végül elvetette a reversion nevet, mert közben ezt a szót valami másnak az elnevezésére kezdte el alkalmazni, helyette a regresszió (regression) elnevezést kezdte el használni erre a jelenségre.
Forrás: Horváth György: Az értelem mérése, Tankönyvkiadó Budapest, 1991





