Ahogyan az egy statisztikai programcsomaghoz illik, az R is rendelkezik mindenféle függvényekkel, amelyek segítségével tulajdonképpen szinte bármilyen eloszlású adatsor esetében képesek vagyunk valószínűségeket oda-vissza kiszámolni. Ráadásul egy az ezekhez használható függvények egy egészen logikus rendszerbe vannak rendezve. Minden egyes eloszlás típushoz 4 különböző függvény tartozik. Mindegyik függvény neve azonos módon épül fel. Az első karakter megadja a függvény funkcióját, ezután pedig az eloszlás nevére utaló karakterek következnek, amelyek az ugyanahhoz az eloszlás típushoz tartozó függvények esetén azonosak.

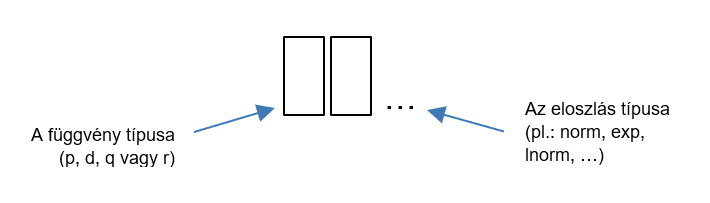
A függvény típusára utaló első betűk jelentése a következő:

• p… – adott x-értékhez tartozó kumulatív eloszlás függvény értéke (probability function)
• d… – adott x-értékhez tartozó sűrűségfüggvény értéke (density function)
• q… – a kumulatív eloszlásfüggvény adott quantilisének értéke, ezzel lehet például egy adott valószínűséghez tartozó x-értéket kiszámítani (quantile)
• r… - megadott mennyiségű adott eloszlású véletlenszámok generálása (random)

Ezeknek a függvényeknek az alkalmazásához szerencsére semmilyen extra programcsomagot nem kell betölteni, mert ezek az alap R részei.

Például a normál eloszlás esetében ez a következőképpen néz ki:

A kumulatív eloszlásfüggvények (p…) esetében a függvény a megadott x-értékhez tartozó valószínűségi értéket adja meg.

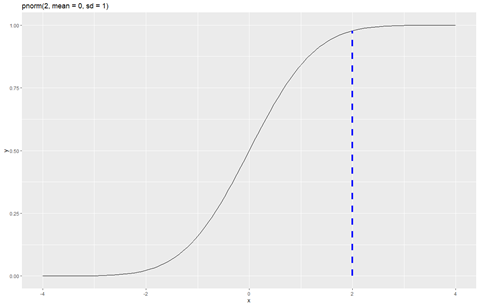
A sűrűségfüggvény alkalmazásával számoló függvény pedig így néz ki.

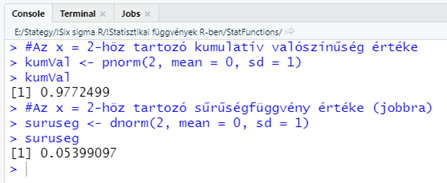
A ’dnorm()’ sűrűségfüggvény esetébenez az x-értéktől jobbra eső görbe alatti területet jelenti.

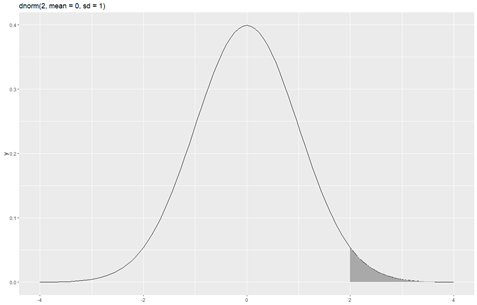
És itt egy fura jelenséget lehet tapasztalni. Azt hinné az ember, hogy a sűrűségfüggvény esetében lehet beállítani azt, hogy a megadott x-értéktől balra vagy jobbra eső terület nagyságát adja meg. Ez sajnos nem igaz, a ’dnorm()’ függvény esetében nem tudunk ilyen módon választani, mert ehhez a függvényhez nem jár ilyen paraméter. Ez persze a valóságban nem okoz akkora pánikot, mert az x-értéktől balra eső terület nagyságát egyébként is megkapjuk, ha a jobbra eső terület nagyságát kivonjuk 1-ből. Ettől függetlenül a személyes véleményem az, hogy a lehetőséget meg lehetett volna adni.

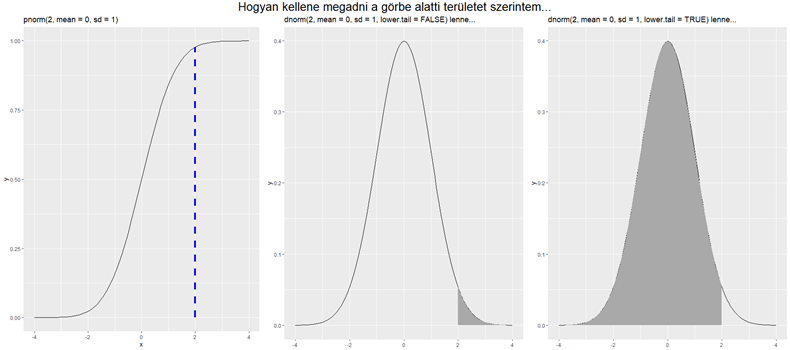
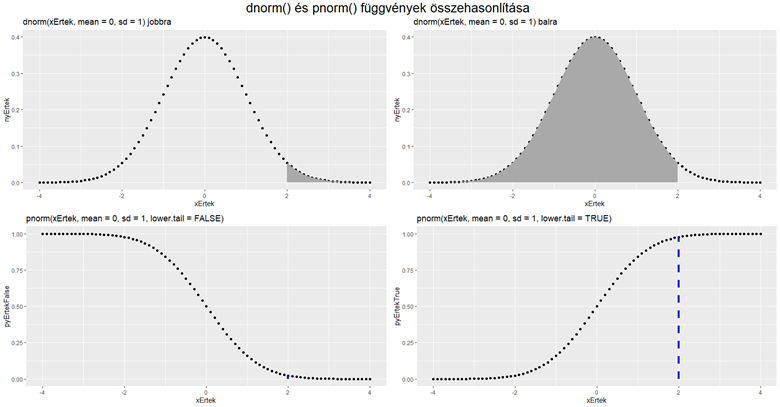
Ezzel ellentétben a ’pnorm()’ függvénynek van ilyen paramétere, ez a ’lower.tail’ paraméter. Ennek IGAZ vagy HAMIS értéket lehet adni (TRUE vagy FALSE). Ha az értéke FALSE, akkor a fenti középső diagramnak megfelelő értéket adja meg, azaz a megadott x-értéktől jobbra eső területet, míg ellenkező esetben a fenti jobboldali diagramnak megfelelően az x-től balra eső területet. De nem így, hanem …

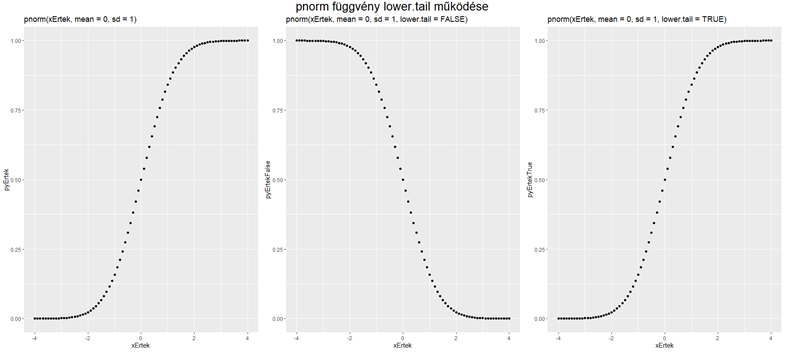
… így. Vagyis amikor a sűrűségfüggvény görbe alatti területének méretére vagyok kíváncsi, akkor a ’pnorm()’ függvény egyszerűen kivonja a kumulatív eloszlásfüggvény értékét 1-ből, és ezt fogja megadni eredményként. A három diagramból jól látható, hogy az alapértelmezés az, ha a ’lower.tail’ paraméter TRUE. Matematikailag teljesen helyes ez a megoldás, semmi gond vele, csak az én világképembe nem passzol bele igazán… Összefoglalva a dolog így néz ki.

A harmadik függvénytípus a ’qnorm()’ függvény, amely tulajdonképpen visszafelé számol. Ha megadok neki egy százalékos értéket, és a normál eloszlás átlagát és szórását, akkor kiszámolja az adott százalékos valószínűséghez tartozó x értékét.

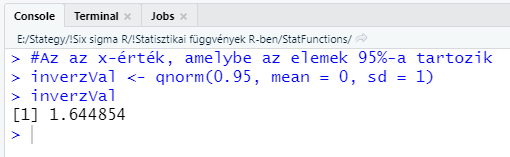
Az alábbi diagram nagyon hasonlít a korábbi kumulatív eloszlás függvényre, de ez esetben az x-, és az y-tengely jelentése felcserélődött. Az x-tengelyen van a valószínűség, az y-tengelyen pedig a keresett érték. Az értelmezése valami olyasmi, hogy a 25%-os valószínűséghez a -0,67 érték tartozik. A függvény nagyon hasonló módon működik, mint például a jól ismert táblázatkezelőben az ’inverz.norm()’ függvény.

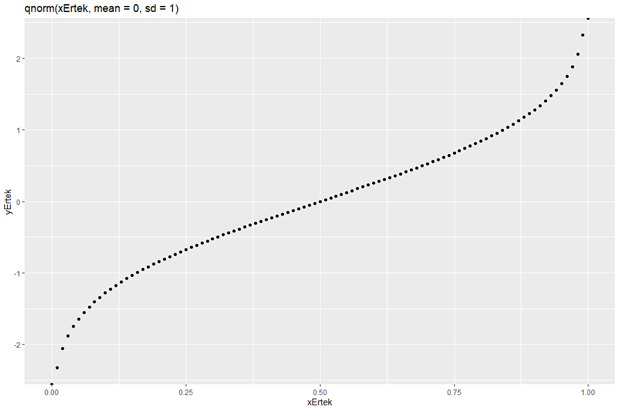
Végezetül lássuk, hogyan működik a normál eloszlású véletlen számok generálása.

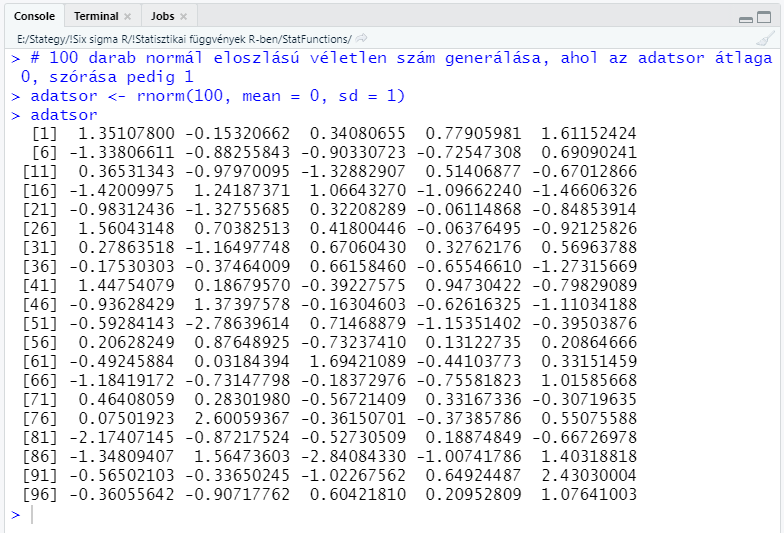
Az alábbi diagram egy quantile-quantile plot, amelyen a korábban generált 100 darab véletlen szám látható. Minél jobban illeszkednek a pontok a diagram átlójában található egyenesre, annál inkább normál eloszlású az adatsor.

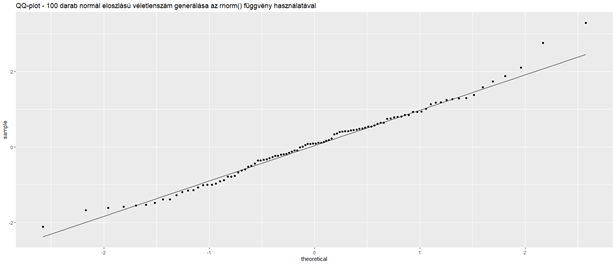
Legvégül idetettem egy listát a különféle eloszlásokhoz tartozó függvényekről. Arra mindenképpen ügyelni kell, hogy a különféle függvényeket különböző paraméterekkel kell alkalmazni, például a Student-eloszlás esetében a ’df =’ paraméterrel kell megadni, hogy melyik t-eloszlást szeretnénk alkalmazni.

 A cikkben található függvények programkódjait most nem ismertettem részletesen, mert a korábbi hetekben írt cikkekhez képest nem sok újdonságot alkalmaztam. A szkripteket viszont le tudod tölteni innen, így a kódokat szabadon megvizsgálhatod és felhasználhatod.

Források:

R documentation: The Normal Distribution
https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/Normal

Data Science Blog: Using probability distributions in R: dnorm, pnorm, qnorm, and rnorm
https://www.datascienceblog.net/post/basic-statistics/distributions/#:~:text=Distribution%20functions%20in%20R&text=The%20four%20normal%20distribution%20functions,function%20of%20the%20normal%20distribution

Probability Distributions in R (Stat 5101, Geyer), University of Minnesota
http://www.stat.umn.edu/geyer/old/5101/rlook.html