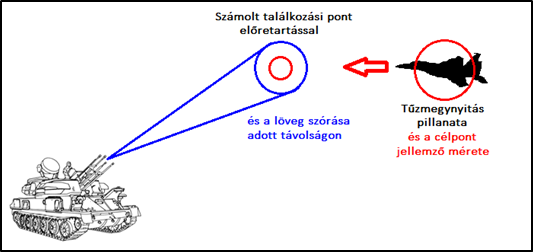
Nemrégen egy nagyon érdekes problémával keresett meg egy úriember, aki olvasta a blogot. A problémája azért egy lehelettel komolyabb a cikkhez mellékelt illusztrációnál, de a kisördög nem hagyott nyugodni, muszáj volt ezt a képet bevágnom ide. A magyar légvédelem azért remélhetőleg ennél magasabb színvonalat képvisel...

A probléma a légvédelmi ütegek találati valószínűségét próbálja meghatározni a célpont mérete és mozgása, a lövedékek szóródása, a célzóberendezés bizonytalansága alapján, és el kell ismernem, hogy nagyon alaposan utánajárt a témának és komoly szakmai igényességgel dolgozta fel a témát annak ellenére, hogy nem katona. A témának ebbe a részébe nem mennék bele mélyebben, hogy elkerüljem a szakmai tévedéseket és pontatlanságokat, mert ezen a területen nem vagyok szakértő. A teljes cikk egyébként elérhető a képre kattintva, vagy ITT:

A szerző a teljes témakör egy kis szeletének megoldása kapcsán keresett meg. Álló célpont esetén a találati valószínűség relatíve jól számolható, ha a fent felsorolt paraméterek valós értékei a rendelkezésre állnak, mozgó célpont esetében viszont a célpont távolságának függvényében változik a találati valószínűség, emiatt mozgó célpont esetében nehéz egy összegzett valószínűséget megadni.

A problémát megpróbáltuk egyszerűen megfogalmazni. A szerző javaslatára azt feltételeztük, hogy van három különböző távolság, egy nagyon távoli, egy közepes távolság és egy közeli távolság. Ha a célpont távolsága a lövegtől nagyon nagy, akkor a találat valószínűsége ~13%. A célpont közepesen messze van a lövegtől, akkor ez a valószínűség ~30%, ha pedig a célpont közel van, akkor ez 50%. Tegyük fel, hogy a célpont közeledik hozzánk. A löveg 3x50 lövést ad le a célpontra. Először akkor lő ki 50 lövedéket, amikor a célpont még nagyon messze van. Másodszor akkor, amikor a célpont közepesen távol van, és harmadszor akkor, amikor már közel van. A kérdés az, hogy mekkora annak a valószínűségem hogy a célpont legalább egy találatot kap a 3x50 lövésből.

Némileg hosszabb gondolkodás után (szégyen, nem szégyen) úgy döntöttem, hogy visszavezetem a problémát egy már jól ismert analógiára:

Tegyük fel, hogy van három kalap, mindhárom kalapban van 50-50 golyó. Ezek egy része fekete, a többi fehér. A fekete golyó jelenti a találatot, a fehér pedig azt, hogy nem talált a lövés.

• Az első kalapban van 6 fekete golyó és 44 fehér golyó, ez reprezentálja a nagyon távoli állapotot, amikor 13% a találati valószínűség.
• A második kalapban 15 fekete golyó van, és 35 fehér golyó, ez jelképezi a 30%-os találati valószínűséget.
• A harmadik kalapban 25 fekete és 25 fehér golyó van, ez jelenti az 50%-os találati valószínűséget.

Ebben az esetben a kérdést úgy tehetjük fel, hogy mekkora annak a valószínűsége, hogy ha minden kalapból húzunk egy golyót, akkor a három kihúzott golyó közül legalább az egyik fekete lesz?

A megoldás első lépéseként át kell fogalmaznunk a kérdést, mert az leegyszerűsíti a megoldás menetét. Igazából az a kérdés, hogy mekkora a valószínűsége annak, hogy mindhárom kihúzott golyó fehér lesz, hiszen ez egyetlen esetet jelent, így ennek kiszámítása jelentősen egyszerűbb és könnyebb. Akkor most vizsgáljuk meg a három húzást egyenként:

• Amikor az első kalapból húzunk, akkor 87% esélyünk van arra, hogy a 44 darab fehér golyó közül valamelyiket kihúzzuk, hiszen 13% annak az esélye, hogy feketét húzunk
• A második kalap esetében a fehér golyó kihúzásának valószínűsége 70%.
• A harmadik kalapból pedig 50%-os valószínűséggel fogunk fehér golyót húzni.

Ha az a feltétel, hogy mindhárom golyónak fehérnek KELL lennie, akkor ennek a valószínűsége a három húzás valószínűségének szorzata, azaz

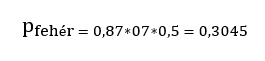
Tehát annak a valószínűsége, hogy mindhárom golyó fehér lesz a kezünkben, kb. 30%. Nyilván minden egyéb esetben lesz legalább egy fekete golyó a kezünkben. Így ha feltételezzük, hogy az összes eset valószínűsége 1, akkor annak a valószínűsége, hogy legalább egy fekete golyó lesz a kezünkben, az

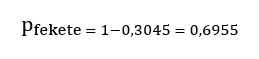
Ezek alapján kijelenthetjük, hogy ~70%-os valószínűséggel legalább egy fekete golyó lesz a kezünkben. Visszatérve az eredeti problémához, ez azt jelenti, hogy ha a fent elmondott feltételek fennállnak, akkor 70% eséllyel legalább egy találat fogja érni a repülő célpontot.

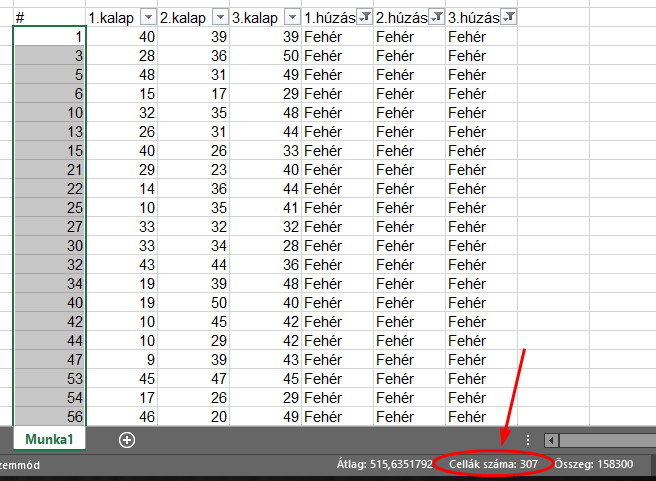
Azért, hogy meggyőződjem róla, hogy helyes a fent vázolt elméletem, újra a táblázatkezelőhöz fordultam. Készítettem három oszlopot a három húzásnak és mindhárom oszlophoz hozzárendeltem egy-egy 1 és 50 közötti véletlenszámot soronként. A következő három oszlopba pedig egy-egy Ha() függvény segítségével beírtam a "Fekete" vagy a "Fehér". Például az első oszlopban a Ha() függvény feltétele az volt, hogy ha a véletlenszámként generált szám 6 vagy annál kisebb, akkor legyen a cellába "Fekete" írva, egyébként pedig "Fehér". Ez reprezentálja a 13%-os valószínűséget. A másik két oszlopban hasonlóképpen generáltam a "Fekete" és a "Fehér" szavakat, csak határértéknek 15-öt, illetve 25-öt adtam meg.

Ezután készítettem így 1000 sort, majd a véletlenszámok rögzítése (kivágás és értékek beillesztése) után leszűrtem, hogy hány olyan sor van, ahol mindhárom húzás fehér volt. Összesen 307 ilyen sort találtam, amely megfelel az előzetesen kalkulált 30%.os értéknek, azaz ha visszafordítjuk a problémát a légvédelmi célpont lelövésére, akkor azt mondhatjuk, hogy az 1000 kísérletből kb. 300 esetben nem érné egyáltalán találat a célpontot..

Összegzés:

Természetesen a valóság még ennél is sokkal bonyolultabb, tehát a tényleges találati esélyek kiszámítása ennél több erőfeszítést igényel, de a különböző helyzetek különböző találati valószínűségének összegzési mechanizmusát a példa jól bemutatja. A fenti linken megtalálható cikkben a szerző ennél sokkal tovább megy, így ez a kis ujjgyakorlat természetesen csak oktatási célokat szolgál.