
Egy korábbi bejegyzésben (Az időtényező – Az idősorok elemzéséről szigorúan szubjektíven) már megemlítettem az autokorrelációt, mint az idősorok elemzésének az egyik eszközét. Most erről a módszerről szeretnék egy kicsit bővebben írni. A korrelációról, mint két adatsor összefüggésének vagy függetlenségének vizsgálati eszközéről már korábban ejtettem szót (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?). De mi a különbség a korreláció és az autokorreláció között? Az auto egy görög szó, amelynek a jelentése „saját” vagy „maga”. Ez alapján az autokorreláció azt jelenti, hogy valami korrelációban van saját magával.
Mit jelent az, hogy egy idősor korrelációban van-e saját magával? Azt, hogy ha mondjuk az idősor minden egyes eleme mellé odatesszük a sorban előtte lévő elemet, és ezt a két adatsort összehasonlítjuk a klasszikus korreláció szabályai szerint, akkor vajon milyen értéket kapunk a korrelációs együtthatóra. Nézzük meg ezt egy példán keresztül.
Az adatsort a cikk végén említett cikkből vettem, amely az ausztráliai Melbourne napi hőmérsékleti adatait tartalmazza 1981 és 1990 között. Az adatsor eleje a következőképpen néz ki:
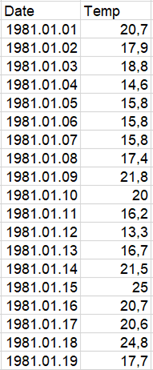
Akkor most minden egyes napi hőmérséklet mellé tegyük oda az előző nap hőmérsékletét a következő módon:
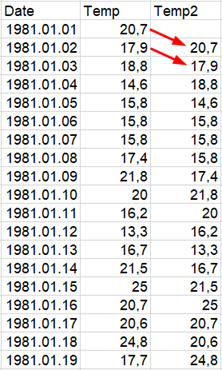
Így kaptunk két adatsort, amelyeknél már a korábban megtanult módon kiszámítható a korrelációs együttható.

Ha a két adatsort egy egyszerű pontdiagramon ábrázolom, akkor a következő ponthalmazt kapom:
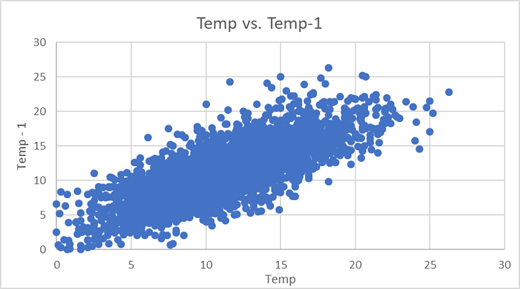
A ponthalmaz alapján rá merném mondani, hogy az adott napi hőmérséklet aránylag erősen függ az előző napi hőmérséklettől. A két adatsor korrelációs együtthatója ennek megfelelően erős pozitív korrelációt mutat, a korrelációs együttható értéke 0,77, amely relatíve közel van a maximális 1-hez. Vagyis az előző nap hőmérséklete erősen meghatározza a következő nap hőmérsékletét. Jó, de mi a helyzet a tegnapelőttel? A két nappal korábbi hőmérséklet mennyire határozza meg az adott nap hőmérsékletét? Hasonló módon elvégezve a tesztet a következőket kapjuk.

A kép nagyon hasonló, de a felhő talán egy kicsit kövérebb. Az aktuális és a két nappal korábbi hőmérsékletek közötti korrelációs együttható 0,63. Ez egy kicsivel kisebb, mint az előző, de a különbség nem túl nagy. A három nappal korábbi hőmérsékletek esetében további hasonló változás tapasztalható:

Az aktuális és a háromnappal korábbi adatok közötti korreláció erőssége tovább csökkent, a korrelációs együttható értéke ez esetben 0,59.
Nos, ezt a végtelenségig lehetne játszani, hiszen az aktuális adatsornak akárhány nappal korábbi adatokkal lehet titkos kapcsolata. A dolog egy kicsit az űrből érkező rádiójelek vizsgálatára emlékeztet, ott is végig pásztázzák a tudósok az összes lehetséges frekvenciát az idegenek jeleit kutatva. Itt is valami hasonló történik, csak ebben a formában nehezen áttekinthető a dolog.
Szerencsére okos tudósok kitaláltak erre egy tömörebb formát, ezt korrelogramnak hívják és az idősorunk esetében ez így néz ki:
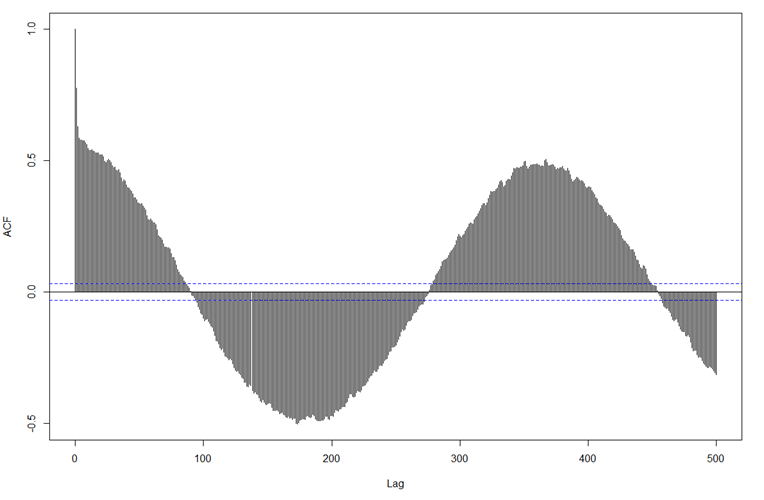
A függőleges tengelyen szereplő ACF rövidítés az „Auto Correlation Function” rövidítése, a vízszintes tengelyen szereplő „Lag” pedig a két adatsor közötti eltolás mértékét adja meg. Az oszlopok természetesen az adott „Lag”-hez tartozó korrelációs együttható értékét mutatja meg. A legelső adat azért mutat egyet mert a program 0-tól és nem egytől kezdi az adatok eltolását, így az adatsor ténylegesen önmagához mért korrelációs együtthatója természetesen 1. A két kék szaggatott vonal az a határ, amelyen belül a két adatsor korrelációja nem számottevő. Egy olyan idősor esetében, ahol az aktuális adatok egyáltalán nem függenek a jelenlegi adatoktól, az összes „Lag” korrelációs együtthatója ezeken a kék vonalakon belül lenne.
A diagram értelmezése az, hogy az aktuális hőmérséklet nagyban függ az azt megelőző napok hőmérsékletétől és minél távolabbra megyünk, ez annál kevésbé igaz. De érdekes módon ez átfordul, hiszen olyan 90 nap után elkezd erősödni a negatív korreláció és olyan 180 nap környékén már egy közepes negatív korreláció van az adatok között. Ezt valahogy úgy tudnám értelmezni, hogy minél hidegebb van télen, annál melegebb lesz nyáron. Persze ez nem ennyire szigorúan igaz, de a -0,5 körüli korrelációs együttható ezt sugallja.
Tanulság, hogy egy ilyen adatsor esetében érdemes vizsgálni a múltbeli adatokat, mert azok alapján – bizonyos határok között – megbecsülhetők a jövőbeni napi hőmérsékleti adatok.
Források:
A Gentle Introduction to Autocorrelation and Partial Autocorrelation By Jason Brownlee on February 6, 2017
https://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/





