
Az előző néhány – a Bayes-tételt bemutató – bejegyzés után végre eljutottam oda, ahová már jó ideje szerettem volna. A szakmában évek óta téma, hogy mennyire hatékonyak a szemrevételezéses ellenőrzések a hibák felderítésében. Arra gondoltam, hogy mi lenne, ha kipróbálnám hogyan lehet Bayes tételét alkalmazni erre a problémára is. Az egész nyilván teljesen elméleti és ezáltal a tanulságok is erős fenntartásokkal kezelendők, különösen az ellenőrzés hatékonyságával kapcsolatos feltételezések. A történet ennek ellenére tanulságos, mert megmutatja, hogy milyen módszerekkel lehetne vizsgálni konkrét ellenőrzési folyamatok hatékonyságát, hiszen minden egyes ellenőrzési módszer különböző és emiatt lényeges eltérések lehetnek a különféle ellenőrzések eredményei között.
Mielőtt belevágok, röviden felsorolom az előzményeket, ha valaki esetleg nem lenne képben. Eddig a következő bejegyzések születtek Bayes tételével kapcsolatban:
- Folt a zsákját! – Thomas Bayes kísérlete – Hogyan találta ki Thomas Bayes tiszteletes a róla elnevezett tételt.
- Üstökös Franciaország egén – Simon Laplace munkássága és Bayes tételének matematikai kidolgozása
- Ha a teszt pozitív, akkor beteg vagyok? – Példa Bayes tételének alkalmazására – Bayes tételének magyarázata és alkalmazásának bemutatása egy egyszerű példán keresztül
A rövid felvezetés után akkor most jöjjön a probléma felvetése. Adott egy gyár, a gyárban előállított minden egyes terméket képzett ellenőrök szemrevételesen ellenőrzik, nehogy hibás termék kerüljön a vevőkhöz. A termékeknek természetesen többféle hibája is lehet, amelyek közül némelyiket könnyebben, másokat nehezebben lehet észrevenni. Példánkban az egyszerűség kedvéért feltételezzük, hogy a gyártás során egyetlen hiba tud előfordulni, ezt az egy hibát kell az ellenőröknek kiszűrni. A korábbi tapasztalatok alapján tudjuk, hogy a hiba a termékek 3%-ánál fordul elő.
A szemrevételezéses ellenőrzésről most azt feltételezzük, hogy az ellenőrzések 80%-ában helyesen dönt az ellenőr. Ha a termék jó, akkor az ellenőr szerint is jó, ha pedig a termék hibás, akkor az ellenőr is hibásnak ítéli meg.
A következőre vagyunk kíváncsiak: Mekkora a valószínűsége annak, hogy az ellenőr jónak ítél meg egy terméket, amely valójában hibás. Ez a hiba a legrosszabb, ami történhet, hiszen egy ilyen esetben nem-megfelelő kerül kiszállításra a vevőnek.
Ebben az esetben az esemény (E) az, hogy az ellenőr a terméket jónak ítéli meg, az ok pedig az, hogy a termék hibás. Ez így most egy kis logikai bukfencnek tűnik, hiszen hogyan lehet oka az ellenőr helytelen döntésének az oka az, hogy a termék hibás? De szerintem ez itt csak nyelvtanilag fura, ettől a gondolatmenet jó. Gondoljunk vissza az előző bejegyzésben ismertetett betegséges – tesztes példára. Ott az esemény az volt, hogy a teszt kimutatta a betegség jelenlétét, míg az ok az volt, hogy a vizsgált személy valóban beteg. Ez így logikusnak tűnik, de ez tulajdonképpen a négy lehetséges eset egyike.

vagy másképpen
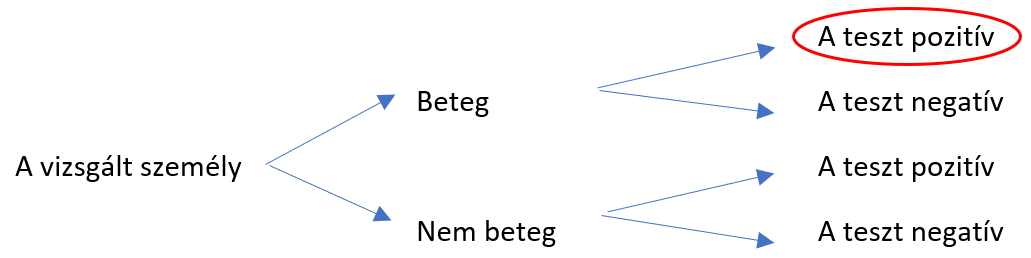
Vagyis a fenti példa csak egy a négy lehetséges kimenetel egyike. Ugyanez igaz a jelenlegi ellenőrzéses példánkra is, csak itt egy másik lehetséges kimenetelt vizsgálunk, nem azt, amit az előzőben:

Emlékeztetőül most nézzük meg még egyszer hogyan is néz ki Bayes tétele:

Akkor most mit is jelentenek a képlet egyes elemei?
P(C|E) annak a valószínűsége, hogy az ellenőr a terméket jónak minősíti, de az valójában hibás.
P(E|C) annak a valószínűsége, hogy ha a termék hibás, akkor azt az ellenőr jónak fogja minősíteni. Mivel fentebb tisztáztuk, hogy az ellenőr az esetek 80%-ában helyesen dönt és 20%-ában helytelenül, ezért itt most a helytelen döntés valószínűsége 20%, azaz 0,2 lesz.
Pprior(C) annak a valószínűsége, hogy a termék hibás, vagyis ez esetben ez 3%, azaz 0,03.
P(E|~C) annak a valószínűsége, hogy az ellenőr jónak minősíti a terméket, amikor az tényleg jó, ez 80%, vagyis 0,8.
Pprior(~C) pedig annak a valószínűsége, hogy a termék jó, ez a termékek 97%-ánál igaz, vagyis ez 0,97 lesz.
Mindezeket a fenti képletbe behelyettesítve a következőt kapjuk:
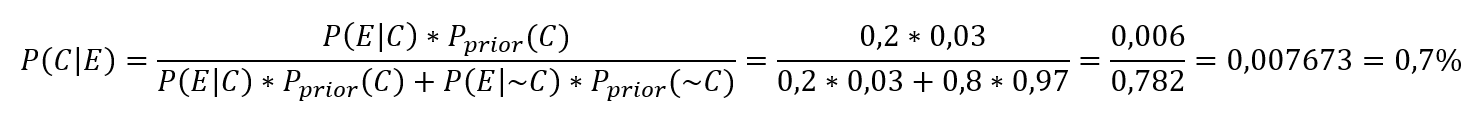
Ez azt jelenti, hogy kevesebb, mint 1% az esélye annak, hogy ilyen feltételek mellett rossz termék fog kimenni. Őszintén szólva sokkal rosszabb eredményre számítottam, a másik oldalon viszont örülök, hogy a szemrevételezéses ellenőrzés nem annyira rossz, mint amilyen rossz véleményem van róla. Persze amennyiben megváltoznak a feltételek, akkor megváltoznak a valószínűségek is. Ha például a selejtarány nem 3%, hanem 30%, akkor a hibás termékek kiengedésének valószínűsége ennek megfelelően fog változni:
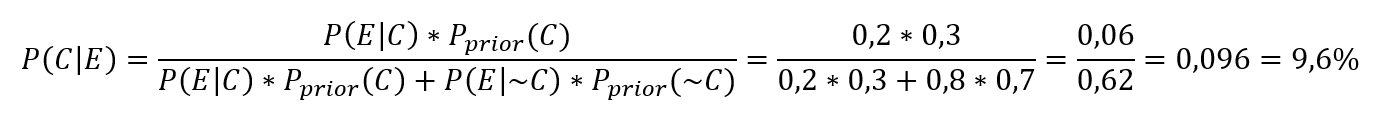
Érdekes lehetséges konklúzió az, hogy ha alacsony a hibaarány, akkor még egy kevésbé hatékony ellenőrzés esetén sem fog túl nagy eséllyel kicsúszni hibás darab. Ha a hibaarány viszont magas a gyártott tételben, akkor még egy hatékonyabb ellenőrzés esetén is jelentősen megnő a hibás termékek kiszállításának veszélye. Ez persze valahol logikus is, hiszen minél kevesebb a hibás darab a tételben, annál kisebb a valószínűsége annak, hogy egy vagy több kikerül a vevőhöz. A fenti következtetések megerősítik a hibák keletkezésének csökkentését célzó tevékenységek létjogosultságát, hiszen a fenti számok is bizonyítják, hogy a belső hibák csökkentésével eredményesebben lehet megvédeni a vevőt a hibás termékek kiszállításától.
Végezetül nézzük meg azt, hogy mi történik akkor, ha egy magas hibarátájú tételt két egymástól független ellenőrzésnek vetünk alá. Az első ellenőrzés eredménye 30% selejtarány és 50%-os hatásfokú ellenőrzés esetén
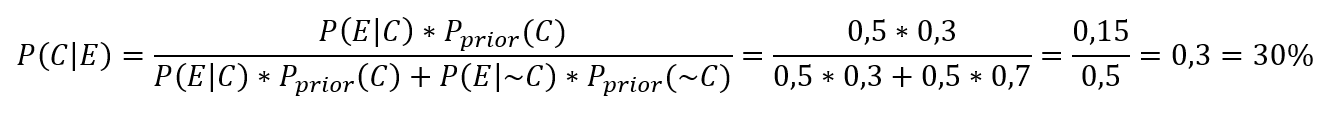
Ez egy igen rossz folyamat, nagy a valószínűsége annak, hogy a hibás termékek eljutnak a vevőhöz. Mi lesz a hatása ez esetben annak, ha bevezetünk egy második ellenőrzést is. A fenti számításból kiderült, hogy a hibás termékek kb. 1/3-a át fog csúszni az ellenőrzésen. Azaz minden 100 darab termékből átlagosan 20 darab fennakad a teszten, 10 darab hibás viszont átmegy. Így a második ellenőrzésre marad mondjuk 80 darab termék, amiből 10 potenciálisan hibás, amely átsiklik az ellenőrökön. Ez így 12,5%-os hibaarányt jelent a második ellenőrzésre. Ezt Pprior(C) helyére behelyettesítve a következőt kapjuk:
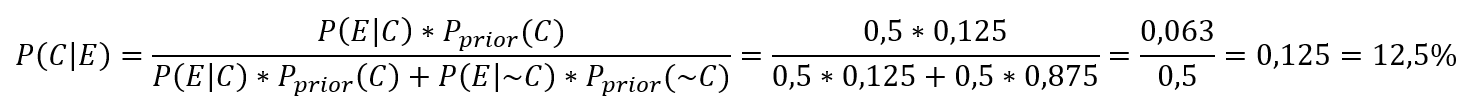
Így a kétszeri ellenőrzés után a megmaradt 12,5%-os hibaaránynak már csak a 12,5%-a fog átjutni a kétszeres szűrőn, ami azt jelenti, hogy a megmaradt 10 hibás termékből már csak 1 vagy 2 fog átcsúszni az ellenőrzésen, amely így a rosszabb esetben 2/72 = 0,027, vagyis kevesebb, mint 3%-os hibaarányt fog jelenteni a vevőnél.
Tehát az egyszeres ellenőrzés során 12,5% lett volna a hibaarány a vevőnél, a kétszeres ellenőrzés után ez már 2,7%-ra javult. És ebben a példában az ellenőrzés hatékonyságára adott 50% pokolian rossz érték. És még egy ilyen kevéssé hatékony ellenőrzésnél is ennyit javít egy második, független ellenőrzés a vevőhöz kiszállított termékek minőségi színvonalán.
Amennyire tudom, Bayes tételének ilyen alkalmazása nem ismert széleskörben a szakmán belül, de mindenképpen figyelemreméltó a módszer. Mivel a gyártott termékek hibaaránya általában jól mérhető, az ellenőrzések hatékonysága szintén meghatározható a megfelelő ellenőrző rendszer elemzési módszerek alkalmazásával, ezért az ilyen jellegű valószínűségi vizsgálatoknak van helye a gyártással kapcsolatos minőségbiztosítási gyakorlatban. Ha mindent jól számoltam…





