Az előző cikkben (Ha nem normál eloszlás, akkor micsoda? – Valószínűségi eloszlás azonosítása R-ben) ott fejeztem be, hogy sikerült elsajátítani egy becslési eljárást a vizsgált adatsor eloszlására vonatkozóan. Ez azonban még igen messze van attól, amit valójában el szeretnénk érni, hiszen az előző cikkben bemutatott módszer csak egy becslést ad az adatsor eloszlására vonatkozóan, de nem adja meg egyértelműen, hogy

• Az adatsor melyik eloszlással írható le a legjobban, és mik a paraméterei annak az eloszlásnak, amely a leginkább illeszkedik az adatainkra
• Milyen bizonyítékok alapján tudjuk azt állítani, hogy ez a bizonyos eloszlás a megadott paraméterekkel valóban elég jól illeszkedik a vizsgált adathalmazra.

 A vizsgálat elvégzéséhez az előző cikkben létrehozott adatokat fogom alkalmazni. Azért, hogy ne kelljen ellapozni az előző bejegyzéshez, bemásolom ide a különböző eloszlású adatsorok létrehozásához szükséges parancsokat.

A vizsgálathoz ismét szükségünk lesz a ’fitdistplus’ csomagra, ezért érdemes ezt is betöltenünk.

Kész vagyunk az előkészületekkel, térjünk a tárgyra. A ’fitdistrplus’ csomagban van egy olyan függvény, amely egy előre megadott eloszlástípust próbál ráilleszteni a vizsgált adatsorra, ez a ’fitdist()’ függvény. Például próbáljunk meg ráilleszteni egy egyenletes eloszlást a fentebb létrehozott ’uniadat’ nevű adatsorra.

Az első sor ráilleszti az ’uniadat’ adatsorra egy egyenletes eloszlást („unif”) és az eredményt elhelyezi az ’unieloszlas’ nevű változóban. A második sor pedig kiírja az illesztés végeredményét. A harmadik sor pedig egy négy különféle diagramból álló vizuális összefoglalót ad vissza, amelyet a későbbiekben részletesen bemutatok majd. De előbb lássuk, hogy mit ad vissza a második sor.

Az eredmény első sorában található a vizsgálat leírása. A ’ Fitting of the distribution ' unif ' by maximum likelihood’ azt jelenti, hogy a vizsgálat célja az volt, hogy maximum likelihood becslés (Ruhát a meztelen királyra! – Maximum Likelihood becslés) alkalmazásával ráillesszen egy egyenletes eloszlásfüggvényt az adatsorra. A 2-5 sorokban megadja az eloszlásfüggvény paramétereit, jelen esetben értelemszerűen az adatsor minimumát és maximumát. Ez természetesen összhangban van az eredeti adatsor létrehozásához használt 0 és 10 értékekkel. A hatodik sor már kínaiul hangzik. Az itt található három érték tájékoztató jellegű, önmagukban nem mondanak semmit sem az illeszkedés minőségéről, csak akkor beszédesek, ha két vagy több különféle illeszkedést szeretnénk összehasonlítani, hogy melyik a jobb. Például, ha a fenti egyenletes eloszlású adatsorra egy normál eloszlás függvényt próbálok illeszteni, akkor a következőt kapom.

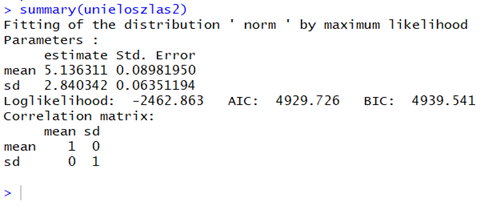
A kétféle illeszkedési riportot összehasonlítva azt látjuk, hogy ha kevésbé illeszkedik az adott eloszlás az adatainkra, akkor a ’Loglikelihood’ az ’AIC’ és a ’BIC’ értékei magasabbak lesznek. Az a cél, hogy olyan eloszlást találjunk, amelynél ez a három érték minél kisebb legyen. Ezek az értékek fontosak, de lejjebb be fogok mutatni ennél hatékonyabb módszert is.

------------

Sajnos ide kívánkozik még egy apró kiegészítés a 'fitdist()' függvény alkalmazásával kapcsolatban. Sajnos van néhány olyan eloszlástípus, ahol a 'fitdist()' függvény egy ilyen egyszerű paraméterezéssel hibára fut. Nézzünk erre egy példát.

Ez az a pont, ahol bámul a felhasználó, mert fogalma sincs arról, hogy most mi a hiba. Az "Unknown starting values for distribution chisq" üzenet azt takarja, hogy a 'fitdist()' függvény írói a khí-négyzet eloszlás esetében nem adtak meg egy olyan kezdőértéket, amelytől elindulva a függvény iteratív módon ki tudja számolni a keresett függvény paramétereket. Vagyis a függvény egy olyan becsült függvényparamétert keres, amely relatíve közel van ahhoz,amit várunk tőle, hogy kiszámoljon. A khí-négyzet függvény paramétere a szabadsági fok (df - degrees of freedom). Jó, akkor megadom neki a 'df = 1'-et, mint paramétert.

Visszajött ugyanaz a hibaüzenet. Akkor most nem ezt kéri? De igen. Csak nem mindegy, milyen formában adjuk meg neki. Azt, hogy 'df = 1' ebben a formában nem eszi meg. A 'fitdist()' függvény leírásában (fitdist function | R Documentation) említésre kerül egy 'start =' nevű paraméter, a leírás szerint itt kell megadni a kezdőértéket az iterációhoz. Akkor megpróbálom így.

Jaj, de jó! Ismét hibaüzenettel tért vissza, de most azt reklamálja, hogy a 'start =' argumentum típusa nem megfelelő. De akkor hogyan kell megadni a 'df' paramétert? Hát így:

Mivel a különféle eloszlásfüggvények esetében sem a függvényparaméterek száma, sem pedig a típusa nem ugyanaz, ezért a függvény egy listát vár a 'start =' paraméter után. Igaz, hogy ennek a listának most ez esetben egyetlen eleme van, de akkor is egy lista típusú adatot kell megadnunk. Úgy tűnik, hogy az ilyen függvények írói számára ez egy természetesen tudott információ, ezért a függvény dokumentációjában ezt sehol sem említik meg (vagy csak én nem találtam meg ezt így explicit módon leírva). És mi van akkor, ha nem tudjuk, hogy mennyi a keresett szabadsági fokok száma? Mondjuk megadok df = 3-at?

Nem történt katasztrófa, a maximum likelihood metódus tette a dolgát és ugyanúgy megtalálta a keresett paramétert. A két eredményt összehasonlítva azt látjuk, hogy nincs köztük különbség.

------------

De most lépjünk eggyel tovább és nézzük meg, hogy mit csinál a fenti kód harmadik sora a ’plot()’ függvény. A fenti kód harmadik sorát lefuttatva a következő diagramokat kapjuk.

Ezek a diagramok már sokkal beszédesebbek. Tulajdonképpen mind a négy diagram a vizsgált adatok elméleti és a gyakorlatban tapasztalt eloszlását hasonlítja össze.

• A bal felső diagram a legkönnyebben értelmezhető, itt az adatsor hisztogramjára van ráfektetve az elméleti eloszlás sűrűségfüggvényének a görbéje a ’fitdist()’ függvény által megadott paraméterek alkalmazásával. Ez esetben jól látható, hogy az elméleti egyenletes eloszlás „görbéje” – azaz az egyenletes eloszlás egyenese – szépen illeszkedik a tapasztalati adatok hisztogramjára.
  
  
• A jobb felső grafikon a már korábban tárgyalt Q-Q plot, amely az x-tengelyen az elméleti, az y-tengelyen pedig a gyakorlatban tapasztalt eloszlás kapcsolatát adja meg az elméleti és a tapasztalati SŰRŰSÉGFÜGGVÉNYEK összehasonlításával. A folytonos vonallal rajzolt egyenes jelöli azt, ahol az elméleti és a tapasztalati eloszlás értéke megegyezik. A fekete pontok által kijelölt vonal pedig az adatsor pontjait adják meg egy kicsit eltorzított koordinátarendszerben (Ne lógjon ki senki a sorból! - Miért fontos, hogy az adatok normál eloszlásúak-e?).
  
  
• A bal alsó diagram hasonló a bal felsőhöz, csak ez esetben nem a sűrűségfüggvényeket, hanem a KUMULATÍV ELOSZLÁSFÜGGVÉNYEKET fektetjük egymásra. Véleményem szerint kicisvel látványosabb lenne, ha a tapasztalati adataink kumulatív hisztogramként lennének ábrázolva, de így is észlelhetők lesznek az eltérések, ha tudjuk, hogy mire figyeljünk.
  
  
• A jobb alsó diagram, amelyet itt P-P plot-ként jelöl a program, majdnem ugyanaz, mint a jobb felső Q-Q plot, de itt nem az elméleti és tapasztalati sűrűségfüggvényeket, hanem a KUMULATÍV ELOSZLÁS-FÜGGVÉNYEKET hasonlítjuk össze. A diagram közepén látható egyenes itt is azt a vonalat jelöli, ahol az elméleti és a gyakorlati értékek megegyeznek.

Azért célszerű a Q-Q és a P-P plot-okat is ábrázolni, mert a Q-Q plot inkább az eloszlások két szélén lévő különbségeket emeli ki, míg a P-P plot az eloszlások közepén lévő eltéréseket domborítja ki jobban.

Mindez érthetőbbé válik, ha kirajzoltatom ugyanezeket a diagramokat arra az esetre, amikor az egyenletes eloszlású adatsorra egy normál eloszlás függvényt próbálok ráilleszteni.

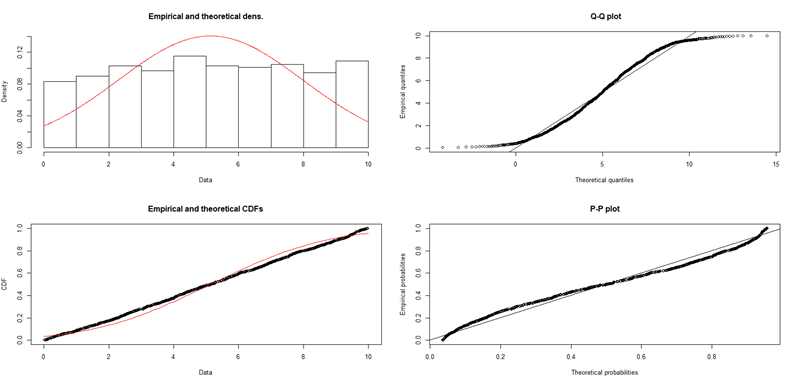
A bal felső diagram magáért beszél, a normál eloszlás sűrűségfüggvénye egyáltalán nem fekszik rá az egyenletes eloszlású adatok hisztogramjára. A Q-Q plot-on az egyenletes eloszlású adatpontok egyáltalán nem fekszenek rá az egyenesre, különösen az eloszlás két végén vannak különbségek, mert ahol az elméleti eloszlásfüggvény alapján már nem lenne szabad értékeknek lenniük, ott még bőven vannak.

A P-P plot esetében szintén látható az eltérés (talán nem annyira szembetűnő, mint a Q-Q plot esetében), de inkább a diagram középső részén.

Nézzük még meg, hogyan néz ki, ha egy normál eloszlású adatsorra próbálok normál eloszlás függvényt ráilleszteni.

Ezek a diagramok már sokkal látványosabbak, mint a fentebb listázott ’Loglikelihood’, ’AIC’ és ’BIC’ értékek, de még ez sem jelent perdöntő bizonyítékot arra vonatkozóan, hogy az adatsorunk, amelyről persze jelen esetben tudjuk, hogy egyenletes eloszlású, hogy tényleg az. Jó lenne valamilyen hipotézis vizsgálat, amely ad egy egyértelmű döntési kritériumot arra vonatkozóan, hogy az adatsorunkra tényleg illeszkedik-e az általunk modellként választott elméleti eloszlás. A ’fitdistrplus’ csomag sajnos erre nem nyújt kielégítő megoldást, ezért egy újabb csomagot vagyunk kénytelenek alkalmazni. Ez az ’EnvStats’ csomag, amit valószínűleg telepítenünk is kell, illetve be kell tölteni a rendszerbe.

Ez egy olyan függvénykönyvtár, amely környezeti statisztikák készítésére szolgál, viszont többek között egy olyan függvényt is tartalmaz, amely megfelel a céljainknak. Ez a ’gofStat()’ függvény, amelyet ismételten egészen egyszerűen tudunk használni arra, hogy leteszteljük, milyen eloszlást követ az adatsorunk. Ha begépeljük vagy bemásoljuk az RStudio-ba a következő parancsot (feltéve, hogy elvégeztük a fenti adatsorok létrehozását), akkor egy részletes riportot kapunk.

Ahhoz, hogy értelmezhető eredményt kapjunk, legalább három dolgot kell megadnunk a függvénynek.

• Az adatsor nevét, amelyet vizsgálunk,
• az eloszlás típusát, amelyet rá akarunk illeszteni az adatsorra, és
• a teszt típusát, amelyet alkalmazni szeretnénk.

Jelen esetben a függvénnyel az egyenletes eloszlású adatsorunkat szeretném ellenőrizni, egy egyenletes eloszlás függvényt szeretnék ráhúzni és a Shapiro-Wilk tesztet szeretném alkalmazni az illeszkedés jóságának ellenőrzésére. Eredményként egy részletes riportot kaptam, amely mindent tartalmaz, amire szükségem van.

Ami fontos ebből, az az egyenletes eloszlás becsült paraméterei, amelyek szerencsére megegyeznek a korábban kapott eredményekkel, illetve a P-value (A titokzatos P színre lép – Mi az a P-Value?), amely végül segít abban, hogy el tudjam dönteni, vajon illeszkedhet-e a megadott eloszlásfüggvény az adataimra. Jelen esetben a P-value értéke 0,608, amely jóval nagyobb, mint a megbízhatósági határként választott 0,05 (95%-os megbízhatóság esetén), vagyis a nullhipotézist, mely szerint az eloszlásfüggvény illeszkedik az adataimra, nem tudom elvetni. Most nézzük meg, mit kapunk akkor, ha ugyanerre az adatsorra ugyanígy egy egyenletes eloszlás függvényt próbálunk illeszteni, de nem a Shapiro-Wilk, hanem az Anderson-Darling tesztet alkalmazzuk.

Ahogy azt láthatjuk, az eredmény igen hasonló lett. Most próbáljunk meg egy normál eloszlás függvényt ráilleszteni az egyenletes eloszlású adatainkra.

A P-value értéke mindkét esetben egy végtelenül kicsi szám lett, vagyis mindenképpen kisebb, mint a választott 95%-os megbízhatósági határ (0,05). Vagyis a nullhipotézist – azaz, hogy az adatsorunk normál eloszlású – mindkét teszt alapján elvethetjük.

Ha a normál eloszlású adatsorra próbálok egy normál eloszlás függvényt illeszteni, akkor ismételten azt fogom kapni, hogy ez lehetséges, mert a P-value értéke nagyobb, mint 0,05.

Sajnos ezeket a teszteket soronként be kell gépelni és minden egyes riportot egyenként kell megjeleníteni. Praktikus lenne egy olyan összefoglaló jelentés is, amely a különböző tesztek becsült paramétereit és a P-value-k értékeit összeszedik egy táblázatba. Elképzelhető, hogy létezik ilyen, de eddig nem sikerült ráakadnom. További apró nehézség, hogy az eloszlások és a különféle illeszkedési tesztek neveit rövidítésekkel kell jelölni a ’gofStat()’ függvény paraméterei között és ezt külön ki kell keresgetni. Ettől most megkíméllek, ide bemásolom a vonatkozó rövidítéseket.

Eloszlások:

Tesztek:

"sw". Shapiro-Wilk; the default when x is NOT supplied.

"sf". Shapiro-Francia.

"ppcc". Probability Plot Correlation Coefficient.

"ad". Anderson-Darling.

"cmv". Cramer-von Mises.

"lillie". Lilliefors.

"skew". Zero-skew.

"chisq". Chi-squared.

"ks". Kolmogorov-Smirnov; the default when x IS supplied.

"ws". Wilk-Shapiro test for Uniform [0, 1] distribution.

"proucl.ad.gamma". Anderson-Darling test for a gamma distribution using ProUCL critical values.

"proucl.ks.gamma". Kolmogorov-Smirnov test for a gamma distribution using ProUCL critical values.

Összegzés:

Azt kell, hogy mondjam, az adatsorok eloszlásának azonosítására hatékony eszközök állnak rendelkezésre R-ben. A folyamat valamivel bonyolultabb, mint például Minitab-ban, ahol néhány mozdulattal kapunk egy teljes összefoglalót. Az talán nem ennyire információgazdag, viszont a riportok szerintem egy kicsivel praktikusabbak a gyakorlati szakember számára. Az R viszont nyújt egy-két olyan extra funkciót, amely talán kárpótol a valamivel komplikáltabb kezelhetőségért. A másik oldalon viszont eléggé sok időmbe telt, mire minden szükséges információt összeszedtem és megértettem a riportok tartalmát. A fentiek ismeretében viszont már egy kezdő is rövid idő alatt komoly elemzéseket lehet képes létrehozni.

A cikkben alkalmazott R szkripteket innen le tudod tölteni.

Források:

Marie Laure Delignette-Muller, Christophe Dutang: fitdistrplus: An R Package for Fitting Distributions, October 2014
http://www-eio.upc.edu/teaching/adtl/apunts/rstudio-eL1036.pdf

Vito Ricci: Fitting distributions with R, Release 0.4-21 February 2005
https://cran.r-project.org/doc/contrib/Ricci-distributions-en.pdf

Bachioua Lahcene: On Pearson families of distributions and its applications, African Journal of Mathematics and Computer Science Research, Vol. 6(5), pp. 108-117, May 2013
http://www.academicjournals.org/app/webroot/article/article1379928288_Lahcene.pdf

Karl Pearson: X. Contributions to the Mathematical Theory of Evolution. - JI. Skew Variation in Homogeneous Material, Philosophical Transactions of the Royal Society of London. A, Vol. 186 (1895), pp. 343-414
https://bayes.wustl.edu/Manual/Pearson_1895.pdf

Baptiste Auguie: Arranging multiple grobs on a page, 2017-09-09
https://cran.r-project.org/web/packages/gridExtra/vignettes/arrangeGrob.html

Package ‘EnvStats’, October 21, 2020
https://cran.r-project.org/web/packages/EnvStats/EnvStats.pdf