A probléma, amiről most írni szeretnék, eléggé általános, a megoldása azonban nem egyszerű. A statisztikai gyakorlatban gyakran előfordul, hogy rendelkezésünkre áll egy minta adathalmaz, ami persze hasznos és már ebből is egy csomó következtetést le lehet szűrni, de még több lehetőségünk lenne akkor, ha ismernénk egy olyan sűrűségfüggvénynek vagy kumulatív eloszlásfüggvények az egyenletét, amely a lehető legnagyobb pontossággal illeszkedik az adatsorunk eloszlására. Az alcím is tulajdonképpen erre akar utalni, csak ez esetben nem ruhát varrunk a királynak, hanem eloszlást szabunk rá egy adatsorra. Maga a „maximum likelihood” kifejezés is valami ilyesmire utal, mert a jelentése is körülbelül annyit jelent, hogy "leginkább valószínű", vagy „maximális valószínűség”, nem könnyű lefordítani ezt a kifejezést.
Egy korábbi bejegyzésben (Első az egyenlők között – a standard normál eloszlás) már olvashattál valami hasonlót a normál eloszlással kapcsolatban, ahol kiderült, hogy a normál eloszlás függvénygörbéjének helyét az átlag, az alakját pedig a szórás befolyásolja. Vagyis, ha egy adathalmaz normál eloszlású, akkor az adathalmaz átlagának és szórásának ismeretében meg tudjuk adni az adatsorra illeszkedő normál eloszlás függvény képletét, és ennek segítségével ki is tudunk számolni mindenféle hasznos dolgokat. Sajnos nem minden esetben vagyunk annyira szerencsések, hogy az adataink normál eloszlást kövessenek, sok esetben fordul elő, hogy az adatainkra egy valamilyen más eloszlást kell ráillesztenünk, ahol a normál eloszlásra vonatkozó törvényszerűségek nem érvényesek. A mechanizmus viszont hasonló a más jellegű eloszlások esetében is, adott egy függvényképlet és ebben van egy, kettő vagy három paraméter, amelyek befolyásolják a végeredményként kapott függvény alakját, így az nagy rugalmassággal illeszthető rá a legkülönfélébb adatsorokra. A kihívást „csak” az jelenti, hogyan határozzuk meg ezt az 1-2-3 paramétert! Ebben segít a maximum likelihood becslés!
Egy másik korábbi videóban (Az átlag standard hibája) már volt arról szó, hogy egy minta akár végtelen számú sokaságból is származhat, és általában nem tudjuk, hogy konkrétan melyikből is származik.
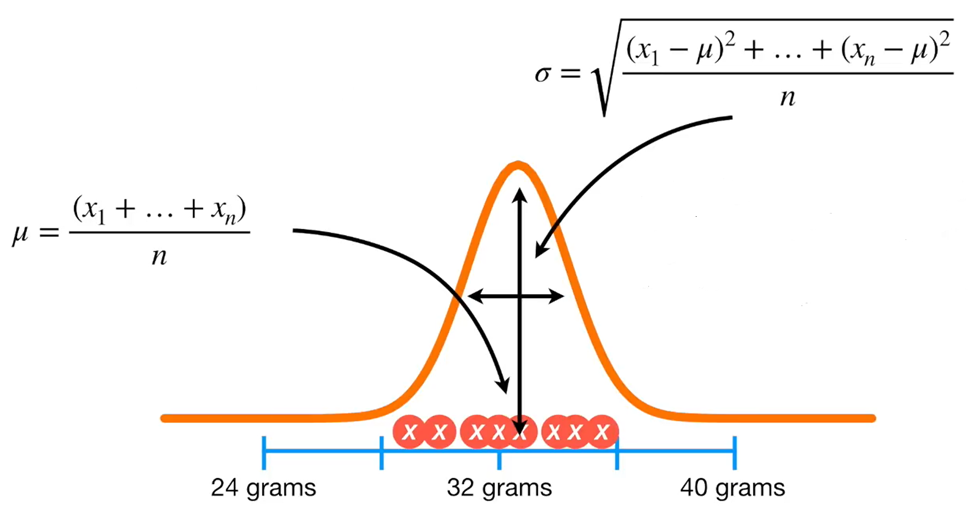
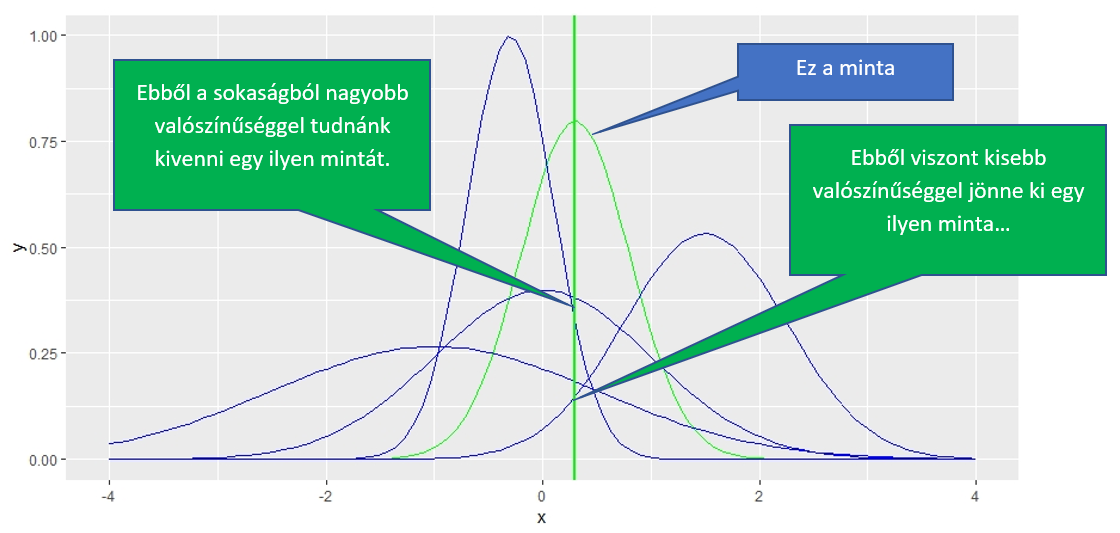Ez alapján azt is aránylag könnyen beláthatjuk, hogy ugyanazt a mintát nem ugyanakkora valószínűséggel vehetjük ki a különféle sokaságokból. A fenti ábrán is jól látható, hogy a az egyik sokaságból egész nagy valószínűséggel, míg egy másikból csak sokkal kisebb valószínűséggel tudnánk kivenni egy ilyen mintát. Ha az elemi lényegét szeretnénk megérteni a maximum likelihood módszernek, akkor azt mondhatnánk, hogy tulajdonképpen folyamatosan változtatjuk az éppen alkalmazott sokaságot és megnézzük, hogy az adott pont mekkora valószínűséggel fordulhat elő az adott sokaságban. Tegyük fel, hogy egerek tömegét vizsgáljuk és a tömegek eloszlását szeretnénk meghatározni. Vegyünk egy pontot, mondjuk azt, ha egy egér tömege 32 gramm és tegyünk rá egy adott sokaságot:
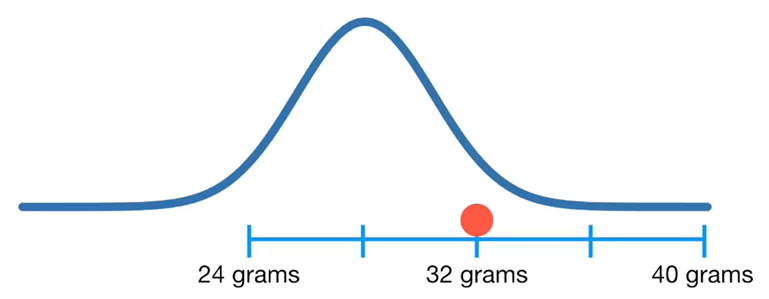
Az adott sokaság esetében annak a valószínűsége, hogy egy egér tömege 32 gramm, egyenlő 0,03-al.
Ezután toljuk el egy kicsit a sokaságot.
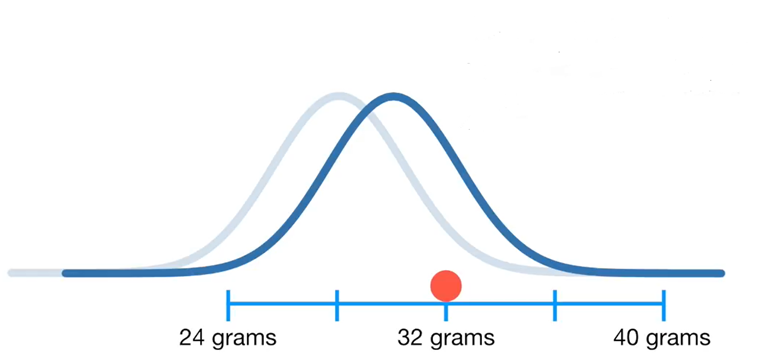
Most nézzük meg újra, hogy mekkora a valószínűsége annak, hogy egy, a sokaságból kivett egér tömege 32 gramm. Amint az látható, a valószínűség 0,03-ról, azaz 3%-ról 0,12-re, azaz 12%-ra nőtt.
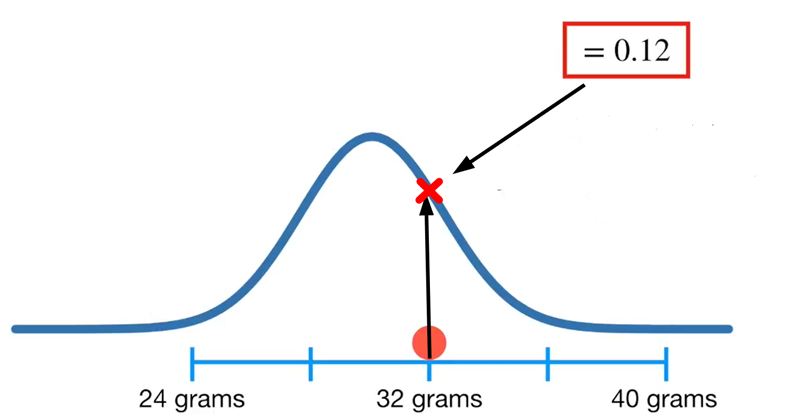
Ha egészen elmegyünk a széléig, akkor egy egészen kis számot kapunk.
Nos, mi lenne, ha rögzítenénk a tesztelt sokaságok szórását egy adott értéken, majd ábrázolnánk a 32 grammos pontra vonatkozó valószínűségeket? A kapott likelihood-függvénynek van egy maximuma, amely nem nagy meglepetésre egybeesik a vizsgálatunk alanyával, azaz a 32 grammal.
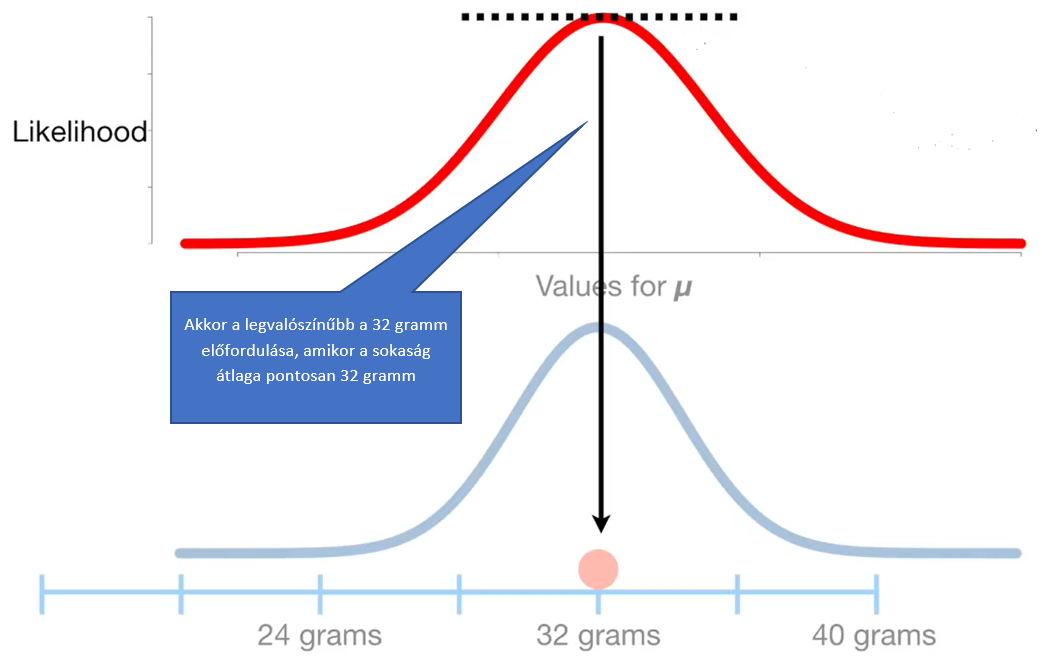
Jó, tehát megtaláltuk az egyik keresett paramétert. A másik keresett paraméter azonban még hiányzik. Természetesen a következő lépésben – felhasználva, azaz rögzítve az előbb megtalált paramétert – most ugyanazt elvégezzük a másik paraméterrel is, azaz a szórással. A szórásról tudjuk, hogy normál eloszlású adatsor esetén nem az eloszlásfüggvény helyzetét, hanem az alakját befolyásolja. Ezért amikor változtatjuk a szórást, akkor a függvénygörbe alakja fog változni.
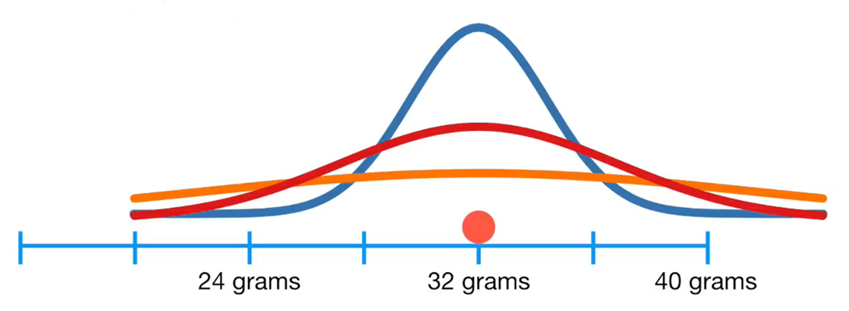
Ha a szórás értékével hasonlóképpen végig próbáljuk a lehetséges értékeket, egy a korábbihoz hasonló likelihood függvényt kapunk:
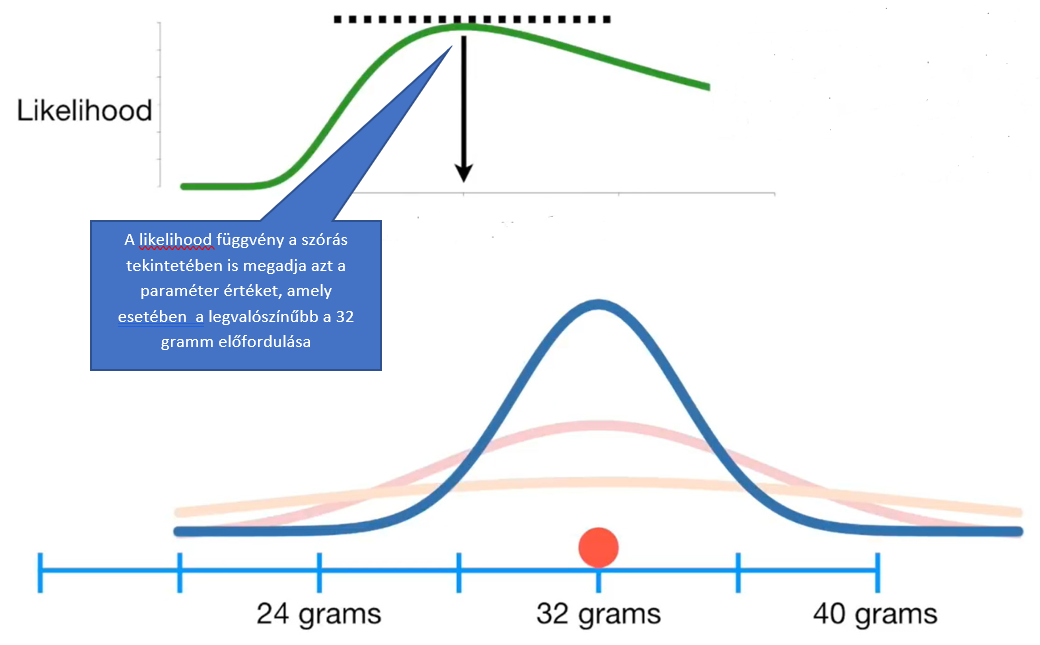
Így most már érthető a módszer alapelve. Természetesen semmi sem olyan egyszerű, mint amilyennek látszik, hiszen általában nem egyetlen pont alapján határozunk meg egy illeszkedő függvénygörbét, hanem egy ponthalmaz alapján!
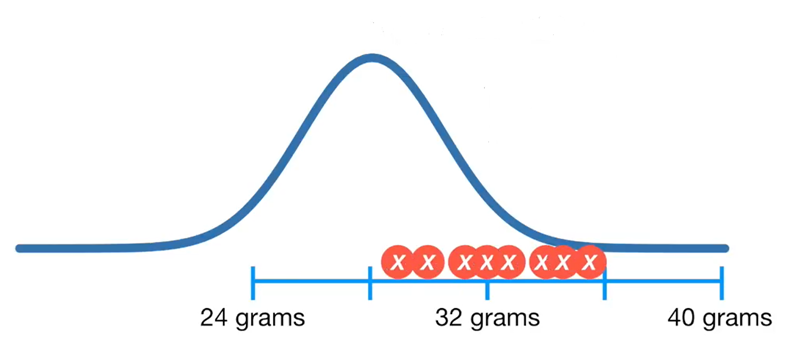
De mi történik ebben az esetben? Ekkor egy adott átlag és szórás esetében minden egyes pontra kapunk egy-egy valószínűségi értéket és a keresett likelihood függvény adott pontját az egyes pontokra kapott valószínűségek SZORZATA adja meg! A függvény paramétereire kapott likelihood függvények így nem azokat a maximumokat adják meg, amelyek a 32 grammra vonatkoznak, hanem az összes pont összes valószínűségére kapott maximum értékeket!
Most persze átugrottam egy nagy csomó különféle levezetést és bizonyítást, amelyek megértése persze igen fontos a módszer eredményes alkalmazásához. A célom viszont elsőre inkább a módszer alapjainak egyszerű ismertetése volt, nem pedig a teljes hátterének bemutatása. Ami viszont még kellemetlenebb, hogy maga a konkrét számítás teljesen másképp működik, a fenti folyamat csak a módszer lényegét mutatja be. A fentiekben alkalmazott átlag és szórás kifejezések, valamint a legutolsó ábrán megadott képletek is csak akkor értelmezhetők, ha azt feltételezzük, hogy a vizsgált adathalmaz normál eloszlású. Más eloszlástípusok esetében a paramétereket is másképp hívják, illetve ezek kiszámítása is teljesen más képletek segítségével történik. És persze arról nem is beszélve, hogy a lineáris regresszióhoz (Miért kevés közöttünk az óriás és a törpe?) hasonlóan itt is mindenképpen vizsgálandó, hogy a kapott függvény ténylegesen mennyire illeszkedik az adathalmaz gyakorisági eloszlására. Ezek a témák viszont nem képezik tárgyát ennek a bejegyzésnek.
Angolul tudóknak a módszer teljesen részletes leírása megtalálható az alábbi videókban:
StatQuest: Maximum Likelihood, clearly explained!!!
StatQuest: Probability vs Likelihood
Maximum Likelihood For the Normal Distribution, step-by-step!
