A múlt heti bejegyzésben (Mi is az a hipotézis vizsgálat) tisztáztuk, hogy miért van szükségünk a feltevésünk indirekt bizonyítására. A következő lépésben azt szeretném bemutatni, hogyan működteti ez az alapelv az egyik legegyszerűbb hipotézis vizsgálatot, az egymintás Z-próbát. Erről a tesztről már volt szó korábban (Z, mint Z-próba… egymintás), a megoldás folyamatát is tárgyaltuk (Számítógépes bowlingozás egymintás Z-próbával). Most azonban a múlt heti bejegyzés szellemében szeretném bemutatni ennek a vizsgálatnak a lényegét.

A probléma erősen hasonlít az előző heti bejegyzésben megfogalmazott kérdéshez:

A kérdés megválaszolása elsőre egyszerűnek tűnhet, de higgyük el, mégsem az. Az, hogy a segéd kivehette a 30 cetlit a kalapból, még nem jelenti azt, hogy tényleg onnan is vette ki, vagyis ez nem egyértelmű bizonyíték. Az viszont az lenne, ha be tudnánk bizonyítani, hogy a segéd nem vehette ki a 30 cetlit a kalapból, vagy legalábbis elenyészően kicsi a valószínűsége annak, hogy ez megtörténhetett.

A feladat fogósnak tűnik, mert egy csomó dolgot nem ismerünk.

• Nem tudjuk, hogy konkrétan milyen számok vannak a cilinderben lévő papírdarabokon.
• Nem láttuk, hogy a segéd tényleg a kalapból vette ki a 30 cetlit
• Nem tudjuk, hogy a segéd igazat mond, vagy hazudik.

A feladat fogósnak tűnik, de aztán a blog szorgalmas olvasóinak esetleg eszébe jut egy réges-régi írás (A nagy dobókocka kísérlet), ahol valami nagyon hasonlót tapasztaltunk, mint a múlt heti cikkben. A sok ezer egyedi dobókocka dobás eredményeinek átlaga 3,5 volt, míg az ebből a sokaságból kivett n-elemű minták átlagai kisebb vagy nagyobb mértékben eltértek ettől a 3,5-től. Amikor viszont rengeteg elegendően nagy elemszámú mintát vettünk ki a dobások sokezres halmazából, akkor ezeknek a mintáknak az átlagait hisztogramon ábrázolva maguk is egy jellegzetes mintázatot rajzoltak ki.

Noha az egyedi dobókocka dobások esetében mind a hat szám körülbelül egyenlő eséllyel jöhetett ki, az átlagok azonban egy haranggörbéhez nagyon hasonló alakzatot vettek fel.

Ezenkívül az is megfigyelhető volt, hogy a mintaátlagok átlaga megegyezett a sokaság átlagával, a mintaátlagok szórása pedig a sokaság szórásának és a mintaszám négyzetgyökének hányadosával.

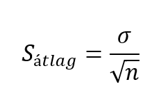
Szerencsénk van, mert ez a jelenség nemcsak a dobókocka dobások esetében figyelhető meg. Szerencsére ez egy matematikailag is bizonyítható általános szabály, igazából teljesen mindegy, hogy milyen eloszlású a populáció, amelyből mintákat veszünk, a mintaátlagok eloszlása elegendően nagy mintaszám esetén mindig normál eloszlás lesz.

Ez az, amelyet most fel tudunk használni a megoldáshoz. Ugyanis ekkor a sokaság átlaga és szórása ismeretében – függetlenül a sokaságban lévő számok konkrét eloszlásától – mindig meg tudjuk mondani, hogy a sokaságból kivett nagy elemszámú minták átlaga mekkora eséllyel mennyi lesz.

Ez esetben viszont azt is meg tudjuk mondani, hogy a minta átlaga mekkora eséllyel mennyi NEM LEHET, ha a mintát ténylegesen abból a sokaságból vettük ki!

Ezek szerint a feladat egyszerű. Ismerve a cilinderben lévő számok átlagát és szórását, ki tudjuk számolni, hogy milyen tartományban lesznek a kalapból kivett minták átlagai. Ha a kezünkben lévő 30 szám átlaga nem esik bele ebbe a tartományba, akkor előáll az egyértelmű bizonyíték, amelyet keresünk. Jó, de hogyan számoljuk ki ezt a tartományt konkrétan? Ehhez ismét elő kell vennünk egy régebbi blogbejegyzést (Ismerd meg a hibafüggvényt! – A normál eloszlás legfontosabb tulajdonságai). Ebben volt arról szó, hogy a normál eloszlás esetében az átlag körüli ± egyszeres, kétszeres és háromszoros szórástartományban található az elemek 68, 95, illetve 99,73 százaléka.

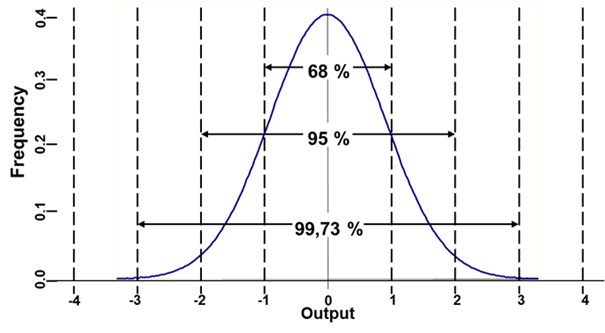
Ha ismerjük a kalapban lévő számok átlagát és szórását, akkor eszerint kijelenthetjük, hogy a kalapból kivett minták átlagainak 95%-a a kalapban lévő számok átlaga körüli ± kétszeres szórás tartományban van. Ha a sokaság átlagát μ-vel, a sokaság szórását σ-val, a kivett minták elemszámát pedig n-nel jelöljük, akkor ezt a tartományt a következő módon tudjuk meghatározni:

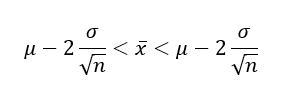
Ezek szerint nincs más dolgunk, mint kiszámítani a kezünkben lévő 30 minta átlagát, illetve a kalapban lévő számok átlagának és szórásának ismeretében kiszámítani a fenti tartományt. Ha a minta átlaga netalán nem lenne benne a fenti tartományban, akkor szerencsénk van, mert kijelenthetjük, hogy 5%-nál kisebb a valószínűsége annak, hogy a kezünkben lévő mintát a segéd a kalapból vette ki, vagyis 100 próbálkozásból kevesebb, mint ötször sikerülne neki ehhez hasonló átlagú mintát kihúzni a kalapból. Szeretném hangsúlyozni, hogy a tankönyvekben nem ez a képlet szerepel, de aki tényleg érti, az nem akad majd ki ezen, mert tudja, hogy a kétféle megközelítés ekvivalens.

Próbáljuk ki a gyakorlatban is, hogyan működik ez a dolog. Az RStudio-ban létrehoztam egy sokaságot, amelynek az a legfontosabb tulajdonsága, hogy minden, csak nem normál eloszlású. Ezt úgy értem el, hogy összekevertem öt normál eloszlású véletlen minta elemeit. Ez így is létrehozható R-ben:

A fenti kóddal létrehoztam a ’sok1’ … ’sok5’ vektorokat, amelyeknek az ’rnorm()’ függvény segítségével adtam értéket. Az ’rnorm()’ függvény alkalmazását már bemutattam egy korábbi cikkben (Ha nem normál eloszlás, akkor micsoda? – adatsor eloszlásának azonosítása R-ben), szóval itt most nem húznám ezzel az időt. A lényeg, hogy a végén a ’sokasag’ nevű változóba összemásolom a ’sok1’ … ’sok5’ változók tartalmát, így az öt darab 200 elemből álló vektorból lett egy darab 1000 elemű vektor, amelynek az eloszlását most már titkosszolgálati eszközökkel sem lehet kideríteni. Íme…

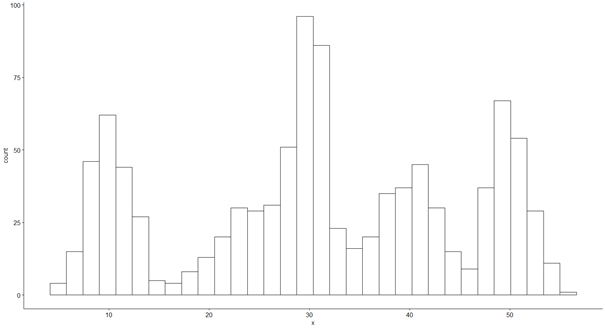
Erre biztosan vannak százszor elegánsabb és valószínűleg hatékonyabb kódok is, de nekem most nem az elegancia, hanem az egyszerűség volt a fontosabb. Amennyiben tudsz ennél jobb vagy gyorsabb kódot erre a célra, akkor megköszönöm, ha kommentben megosztod az olvasókkal.

Akkor most a rend kedvéért nézzük meg ennek az 1000 elemű számhalmaznak az átlagát és a szórását. Merthogy annak ellenére, hogy az adatsor eloszlása többé-kevésbé semmire sem emlékeztet, azért neki is van átlaga és szórása, csak ez (még) most nem mond a számunkra semmit.

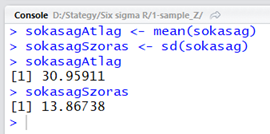
Ezen két számból azonban már ki tudjuk számolni azt a tartományt, amelybe a sokaságból kivett minták átlagait várjuk. Ehhez csak a fentebb leírt képletbe kell behelyettesíteni a sokaság átlagát és szórását. Úgy döntöttem, hogy 100 elemből álló mintákat fogok kivenni a sokaságból. 30-32 elemű minták is elegendőek lennének, de inkább biztosra megyek. A ’mintaAtlagAh’ jelenti a mintaátlagok tartományának várható alsó határát, a ’mintaAtlagFh’ pedig a tartomány felső határát adja meg. Az R-ben nagyon egyszerűen lehet képleteket létrehozni és számolni egyszerű számokkal vagy akár változókkal.

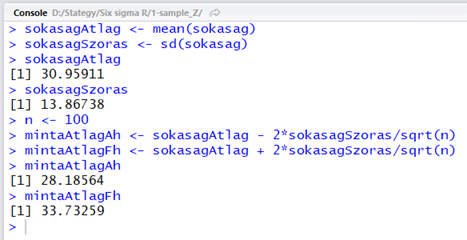
Ok, akkor most megvan a keresett tartomány, ahová a mintaátlagokat várjuk. Következő lépésként vegyünk ki ebből a sokaságból rengeteg mintát. Ez a kód ez kicsivel bonyolultabb lesz, de nem teljesen érthetetlen. Mindenekelőtt leszögezem, hogy nekem most kizárólag a minták átlagaira lesz szükségem, a mintákra magukra nem, ezért azokat nem is fogom elmenteni.

A minták átlagait a ’mintaAtlagok’ nevű változóba fogom elmenteni. Ezt R-ben nem feltétlenül fontos előre létrehozni, de az átláthatóság kedvéért én most létrehoztam. Ezután a ’for()’ parancs alkalmazásával létrehozok egy ciklust, amely készít 1024 darab mintát (azért 1024-et, mert ennek a négyzetgyöke 32). A for-ciklus számlálója az ’i’ változó, a ciklus addig fog futni, ameddig ’i’ értéke el nem éri az 1024-et. A cikluson belüli parancsokat kapcsos zárójellel jelöljük.

• A ciklus első sorában a ’sample()’ függvény segítségével kiveszek a ’sokasag’ nevű változóban elmentett 1000-elemű számhalmazból 100 véletlenszerűen kiválasztott számot. A függvény ’replace = FALSE’ paramétere azt mondja, hogy a kivett mintaelemet a függvény ne tegye vissza, azaz legyen ez egy nem visszatevéses mintavétel (mint a lottószám sorsolás).
• A ciklus második sorában kiszámolom az előzőleg kivett minta átlagát és elmentem az ’atlag’ nevű változóba.
• A ciklus harmadik sorában az ’atlag’ változó értékét hozzáteszem a ’mintaAtlagok’ tömbhöz.
• A ciklus negyedik sorában megnövelem ’i’ értékét eggyel.

Végeredményként kaptunk egy 1024 elemből álló vektort (vagy tömböt), amely fel van töltve a sokaságból kivett minták átlagaival. Hogyan néz ki a mintaátlagok hisztogramja?

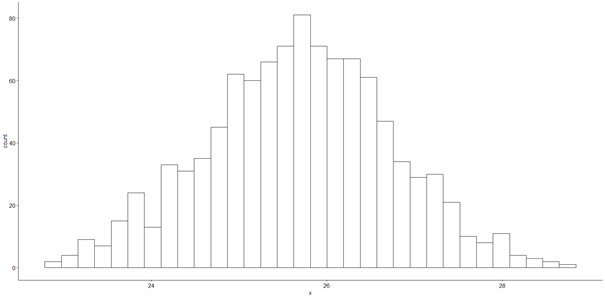
Ez egy láthatóan haranggörbére emlékeztető alakzat. A rend kedvéért azért győződjünk meg arról, hogy a mintaátlagok tényleg normál eloszlásúak. Ehhez ne felejtsük el betölteni a ’normtest’ csomagot. Ha esetleg úgy érzed, hogy érdemes a normalitás vizsgálatokkal kapcsolatos tudásodat felfrissíteni, akkor fusd át a 'Ne hanyagold el! - Normalitásvizsgálatok R-ben' című cikket.

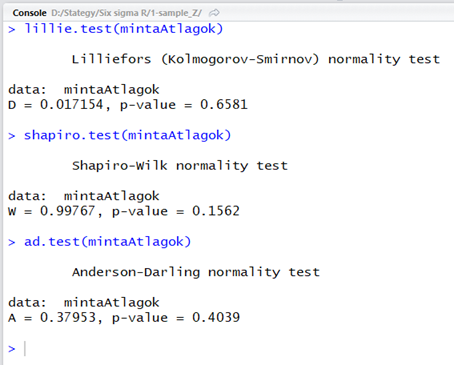
Mivel a ’p-value’ mindhárom esetben nagyobb, mint 0,05, ezért nyugodtan elfogadhatjuk, hogy a teljesen szabálytalan eloszlású sokaságból kivett 100-elemű minták átlagai normál eloszlást követnek. De vajon igaz-e a másik állításom, hogy a mintaátlagok a sokaság tulajdonságai alapján fent kiszámított tartományba esnek? Nézzük meg, mekkora a mintaátlagok legkisebb és legnagyobb eleme.

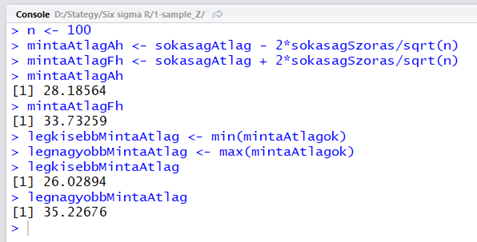
Ha visszalapozol egy kicsit, akkor látni fogod, hogy a legkisebb mintaátlag KISEBB, mint a sokaság tulajdonságai alapján becsült alsó határérték, illetve a legnagyobb mintaátlag is NAGYOBB, mint a sokaság tulajdonságai alapján becsült felső határérték. Akkor most az egész eddigi magyarázat nem igaz?

De, igaz. Mert ugye azt senki sem mondta, hogy a fenti képlet alkalmazásával azt a tartományt adjuk meg, amin kívül biztosan egyetlen átlag sem fog esni. Azt mondtuk, hogy az átlagok 95%-a fog beleesni ebbe a tartományba! Rendben, – mondod kedves okkal gyanakvó olvasó – akkor ez most igaz? Nézzük meg…

Akkor most a ’mintaAtlagok’ változóban szereplő átlagok közül ki fogom szűrni azokat, amelyek a fent megadott 28,1856 és 33,7325 közé esnek.

Ez a sor nagyon trükkös, de megmondom őszintén, nagyon tetszik, hogy egy vektor elemeit úgy is tudom szűrni, hogy a szűrőfeltételt úgy adom meg, mint ahogyan a vektor elemeire szoktunk hivatkozni. Tehát egy vektor elemeire nemcsak sorszámokkal lehet hivatkozni, hanem szűrőfeltételek megadásával is. Ez esetben a mintaAtlagok95 változóba elmentettem a mintaAtlagok vektor azon elemeit, amelyek nagyobbak, mint 28,1856 és kisebbek, mint 33,7325.

Eredményként azt kaptam, hogy a mintaAtlagok95 vektor 987 elemből áll, vagyis az eredeti 1024 átlagból 987 beleesik az előzőleg megbecsült tartományba.

Ez az összes mintaátlag 96,38%-át jelenti. Mivel ez egy kicsivel több is, mint a célul kitűzött 95%, ezért mégiscsak kijelenthetjük, hogy a rendszer működik! A minták átlagai normál eloszlásúak és a sokaság tulajdonságai alapján valóban előre meg lehet mondani, hogy a minták átlagai milyen tartományba fognak esni.

Azonban itt még mindig nem ér véget a történet. Akár véget is érhetne, mert tulajdonképpen megvan az egyértelmű döntési kritérium, amit kerestünk. Érdekes módon azonban a tankönyvekben nemcsak ez a módszer szerepel, hiszen a korábbi cikkeimben én sem ezt az utat választottam, hanem a standardizálást. De akkor miért használjuk a másik módszert is és miért nem csak ezt?

Ez véleményem szerint (merthogy „hivatalos” választ erre még nem találtam) ez azért van, mert a régi időkben, amikor még nem voltak nagy teljesítményű számítógépek, igen nehéz volt egy teljesen általános normál eloszlás esetében kiszámolni egy adott esemény valószínűségét. Az egyetlen standard normál eloszlás esetében viszont a rendelkezésre álltak az előre kiszámolt valószínűségi táblázatok, amelyekből Z értékének ismeretében ki lehetett számolni annak a valószínűségét, hogy egy adott minta átlaga mekkora valószínűséggel vehet fel egy adott értéket. Vagyis ez egy kicsivel több információt ad, mint az általam fentebb ismertetett megbízhatósági tartomány.

Mivel ezt a módszert már leírtam korábban és az erről szóló cikk linkjét is beillesztettem a cikk elején, azért ezt most nem készítem el, inkább arra koncentrálok, hogy hogyan lehet ezt R-ben elvégezni. Szokásosan ehhez sem kell más, mint egy újabb csomag, amelyet most ’BSDA’ néven emlegetnek. A titokzatosnak látszó név a ’Basic Statistics and Data Analysis’ nevet takarja, és Larry J. Kitchens hasonló című könyvének a segédleteként funkcionál. Van a csomagban egy csomó minta adatsor, amikkel játszadozni lehet, de emellett található itt egy-két hasznos függvény is. Ilyen például a ’z.test()’ függvény is, amelyet alkalmazni fogunk. Először is töltsük be a ’BSDA’ könyvtárat.

Ezután létre kell hoznunk egy minta adatsort, amelyet vizsgálni fogunk, hogy kivehettük-e a fentebb már létrehozott ’sokasag’ nevű adathalmazból. Először ténylegesen ebből a sokaságból veszek majd ki egy mintát, hogy lássuk, a teszt tényleg azt fogja hozni, hogy a mintát kivehettük ebből a sokaságból.

A kapott mintát a neve begépelésével meg lehet jeleníteni.

Most pedig a ’z-test()’ függvény alkalmazásával elvégzem az egymintás Z-próbát.

A ’z.test()’ függvény első paramétere a minta saját maga, azaz az egyMinta változó. A sokaság általában nem áll a rendelkezésünkre adatsorként, ezért csak a sokaság átlagát (mu = sokasagAtlag) és a szórását (sigma.x = sokasagSzoras) tudjuk megadni. A ’sigma.x’-ben azért van a ’.x’ mert ezzel a függvénnyel kétdimenziós sokaságot is tudunk vizsgálni, csak akkor az y-irányú szórást is meg kell adnunk. az ’alternative = „two-sided” azt jelenti, hogy kétoldali tesztet kérünk, azaz nem tudjuk, hogy a minta kisebb-e vagy nagyobb a sokaság átlagánál. A ’conf.level = 0,95’ pedig azt jelenti, hogy 95%-os megbízhatósági szinten szeretnénk tudni, hogy a mintát a sokaságból vettük ki vagy sem.

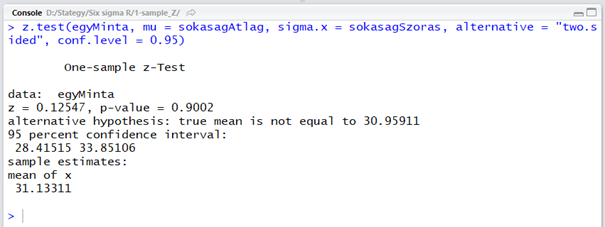
Nos, az eredményt a következő módon tudjuk értelmezni. A ’data: egyMinta’ sor egyértelmű, ez arra szolgál, hogy amennyiben több hasonló tesztet is végzünk, akkor azonosítani tudjuk, hogy melyik teszt melyik. A következő sor természetesen a standardizáláskor kiszámított ’z’ próbastatisztika és a p-value értékét tartalmazza. Csak emlékeztetőül:

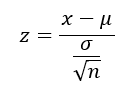
A p-value jelentésének részletes magyarázata pedig ’A titokzatos P színre lép – Mi az a P-Value?’ című cikkben olvashatod el. A harmadik sorban található a nullhipotézis ellenkezője az alternatív hipotézis, amely ez esetben azt mondja, hogy a sokaság átlaga, amiből ezt a mintát kivettük nem egyenlő 30,95911-el, azaz az általunk megadott sokaságátlaggal (csak ez most nem látszik). Az ötödik sorban található a 95%-os megbízhatósági intervallum alsó és felső értéke. Ezek azok, amelyeket fentebb mintaAtlagokAh és mintaAtlagokFh nevekkel illettem (mivel közben időnként újraszámolgattam dolgokat, tizedes eltérések lehetnek az adatok között. Bocs). A riport végén vannak a mintára vonatkozó becsült értékek (sample estimates). Itt csak a minta átlaga jelenik meg, amely ez esetben 31,13311.

A riport eredménye egyrészt az, hogy a p-value jóval nagyobb, mint 0,05. Másrészt a minta átlaga (31,13311) benne van a 28,41515 és a 33,85106 közötti tartományban. Sajnos szöveges kiértékelést nem kapunk, pedig illendő lenne leírni, hogy a nullhipotézist elfogadjuk, azaz nincs elegendő bizonyítékunk arra, hogy a mintát nem az általunk megadott sokaságból vettük ki.

Összegzés:

Azt hiszem, hogy kimerítő mélységben elemeztem ezt az egyébként nem túl bonyolult módszert. Noha a cikk egészen hosszú lett, reménykedem benne, hogy a magyarázat követhető és így érthető lesz mind a próba, mind pedig a teszt megvalósítása R-ben.