A Bernoulli eloszlás Jacob Bernoulli svájci matematikusról kapta a nevét, aki kitalálta a Bernoulli próbát, amely a világ egyik legegyszerűbb valószínűségszámítási kísérlete. Tegyük fel, hogy feldobunk egy darab érmét egy alkalommal. Az érme feldobásának, mint eseménynek kétféle végeredménye lehet. Nevezzük el a kétféle végeredményt k-val, és ha az érme úgy érkezik, hogy a fej van felfelé, akkor ezt nevezzük el sikernek és jelöljük k = 1-gyel, ha pedig az érme az írás oldalával felfelé esik le, akkor ezt értelmezzük kudarcként és jelöljük k = 0-val.

Mondhatnánk azt is, hogy az írás a siker és azt jelöljük 1-gyel és a fej a kudarc és azt jelöljük 0-val, de most ez esetben maradjunk az eredeti változatnál. Mivel az érme feldobásának eredménye vagy fej lehet, vagy pedig írás, de más nem, ezért a kétféle végeredmény valószínűségének összege 100%, azaz 1 lesz.

Mennyiben különbözik a Bernoulli-eloszlás az előző alfejezetben tárgyalt diszkrét egyenletes eloszlástól? Annyiban egyszerűbb, hogy egy eseménynek csak két lehetséges végkimenetele lehetséges, annyiban viszont bonyolultabb, hogy a kétféle végeredmény valószínűsége nem feltétlenül egyforma.

Nevezzük el a fej, azaz a siker valószínűségét p-nek. Az előző kijelentés alapján az írás, azaz a kudarc valószínűsége 1 – p lesz.

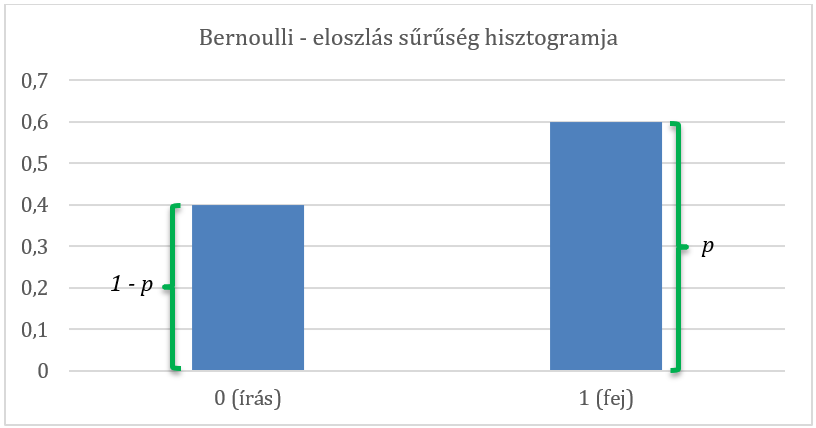
Tehát az érme feldobásának várható eredménye a következő lesz:

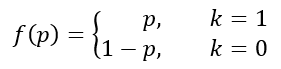
Ezt a képletet úgy fordíthatjuk le, hogy ha k=1, akkor f(p)=p, ha pedig k=0, akkor f(p)=1-p. Az összefüggést felírhatjuk úgy is, hogy

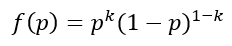
ahol k = 1 vagy k = 0. Vegyük észre, hogy ha k = 1, akkor

és ha k = 0, akkor

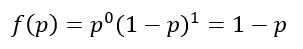
Mi lesz a siker, azaz a fej dobás valószínűségének várható értéke? Ha kiszámítjuk a kétféle várható érték valószínűségekkel súlyozott összegét, akkor azt kapjuk, hogy

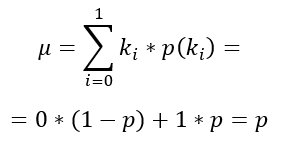
Akkor ez most mit is jelent? µ értéke megadja k várható értékét, tehát azt az értéket, amit nagy számú érmefeldobás esetén az eredmények átlagaként várunk. Próbáljuk ki – hasonlóan a dobókockás kísérlethez – hogy mi történik akkor, ha egy pénzérmét 1000 alkalommal feldobunk. Mivel nincs cinkelt érmém, ezért természetesen az 1000 kísérlet várható értéke nem 0,6 hanem 0,5 lesz, hiszen az érme két oldala egyenlő eséllyel jöhet ki az egyes dobások esetében.

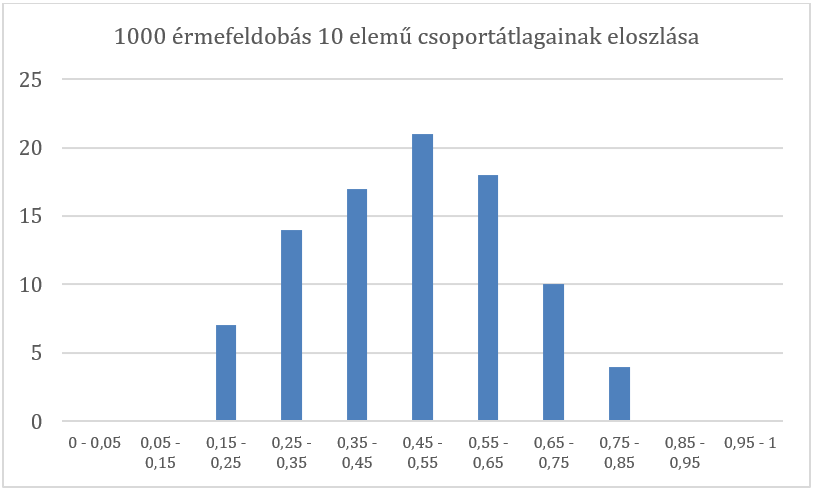
Természetesen az 1000 darab érmefeldobás eredményének átlaga 0,498 (utána lehet számolni), azaz majdnem 0,5 lett, és a fenti diagramon is jól látható, hogy a 10-elemű minták átlagai közül is a legtöbb a 0,45 és 0,55 közötti tartományba esik. Viszont a diagramon az is jól látható, hogy vannak olyan csoportátlagok, amelyek értéke közel sem 0,5. Ez azt jelenti, hogy egy Bernoulli-eloszlás esetén is van a csoportátlagoknak varianciája? A jelek szerint igen.

Most próbáljuk meg kiszámítani ezt a varianciát a korábbi p = 0,6 példa esetében. A varianciát általánosságban az egyes pontok és a µ várható érték közötti különbség négyzeteinek átlagaként értelmezzük. Ebben az esetben ezt a varianciát az egyes pontok és a µ várható érték közötti különbségek előfordulási valószínűségekkel súlyozott összegeként értelmezzük.

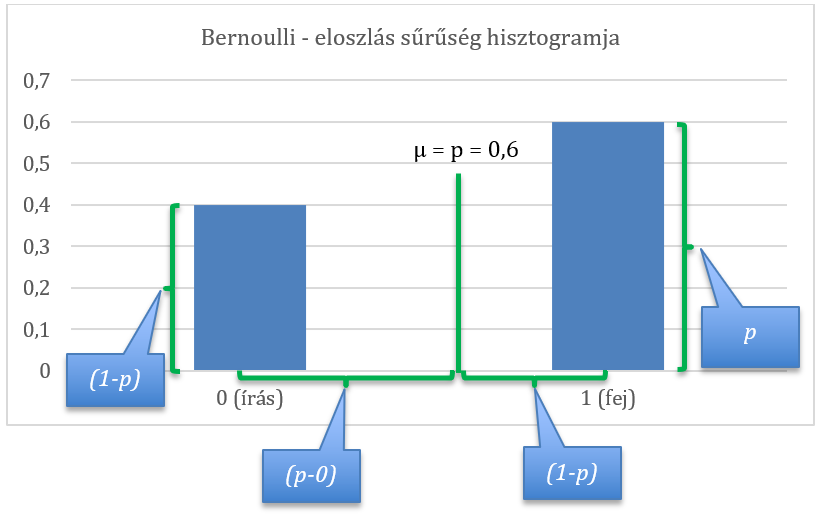
Mivel a lenti képletben ki  értéke vagy 0 vagy pedig 1, µ értéke pedig mindig p, ezért a (ki – µ)2 értéke vagy (p - 0)2 vagy pedig (1 – p)2. Ezeket szorozzuk meg a megfelelő p vagy (1 - p) valószínűségekkel.

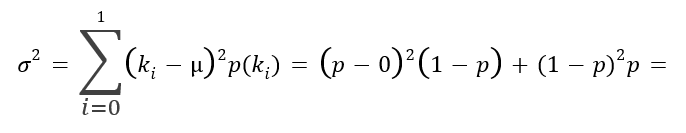
A fenti képletben (p - 0) = p, ennek a négyzete p2, (1 – p)2 pedig (1 - 2p + p2). Ez alapján

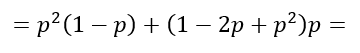
Felbontva a zárójeleket, azaz a zárójeleken belül lévő tagokat külön-külön megszorozva p2-el, illetve p-vel

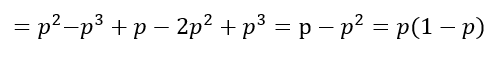
p3 és -p3, illetve p2 és a -2p2-ből az egyik kiütik egymást, így

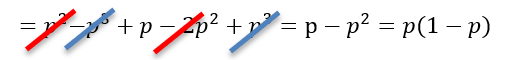
Tehát ezek alapján a fej dobás várható értékének varianciája p(1 – p). Így az érme feldobása esetén a siker, azaz a fej dobás várható értéke 0,6. ez azt jelenti, hogy elegendően nagy számú érme feldobás esetén az esetek 60%-ában lesz fej az eredmény, illetve ennek szórása

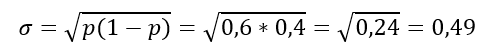
Ez egy igen nagy szórást jelent, hiszen a fejdobás várható értéke 0,11 és az 1, mint természetes határérték között változhat. Ha így nézzük, akkor a várható érték ez esetben nem túl jó becslést ad. Mivel a Bernoulli-eloszlás csak p értékétől függ, ezért minél inkább közelít p értéke 0-hoz vagy 1-hez, annál kisebb lesz a becslés szórása.

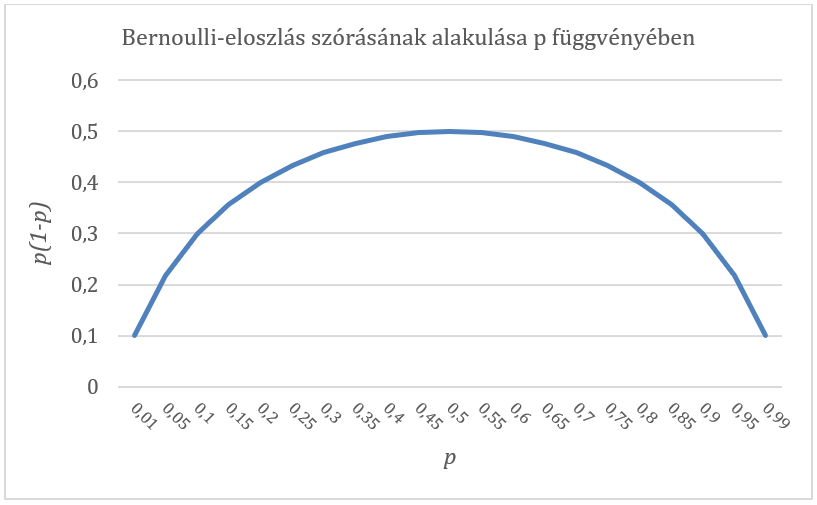
A fenti okfejtés miatt ez jogos is, hiszen, ha mondjuk k várható értéke 0,5 szórása pedig 0 és 1 között változik, akkor k értéke majdnem egyenlő valószínűséggel lehet 0 és 1 is, tehát szinte lehetetlen megjósolni, hogy a következő dobásunk fej lesz vagy írás. Egy későbbi bejegyzésben tovább lépünk és megnézzük, mi történik akkor, ha nem csak egy Bernoulli próbát végzünk el, hanem Bernoulli próbák sorozatát végezzük el és ennek a sorozatnak a tulajdonságait szeretnénk megismerni.