Az egyik előző bejegyzésben (lásd itt) már távolról pedzegettem a témát, hogy jó lenne tudni valamit arról, hogy az adataink milyen eloszlást követnek. A számítógép előtti időkben igen időigényes volt az adatok ábrázolása vagy bonyolultabb számítások elvégzése az adatsorokon. Az igény mégis megvolt arra, hogy valamilyen egyszerű módon következtetni lehessen az adatsor eloszlására vagy legalábbis arra, hogy az adatsor normál eloszlást követ-e vagy sem. Szerencsére a normál eloszlásnak van egy-két olyan tulajdonsága, amelyek segítenek abban, hogy néhány egyszerű számítás alapján legyen egyáltalán ötletünk arról, hogy az adatsorunk normál eloszlású-e vagy sem.

Erre a következő eszközöket tudjuk használni:

- A minimum és maximum értékek, illetve a quartilisek segítségével meg tudjuk becsülni, hogy az adatsor eloszlása mennyire szimmetrikus.

- A ferdeség (skewness) kiszámításával szintén a sűrűségfüggvény szimmetriájára tudunk következtetni

- A lapultság (kurtosis) segítségével pedig arra tudunk következtetni, hogy vajon a sűrűségfüggvény görbéje magasabb vagy alacsonyabb, mint a normál eloszlás görbe.

Ez azt jelenti, hogy néhány jól megválasztott jellemző kiszámításával meg tudjuk becsülni, hogy az adatsorunk normál eloszlású-e vagy sem. Nem tuti biztos a módszer, de ha gyorsan kell egy becslés, és nincs más eszközünk, akkor ezek arra jók.

1.       Ferdeség (Skewness)

Az első pontot a fent említett bejegyzésben már tárgyaltam, ezt nem szeretném megismételni. A második pont egy kicsit bonyolultabb, a ferdeség „hivatalos” definíciója eléggé kínai. Ilyen meghatározásokat lehet találni szerte a neten és a tankönyvekben:

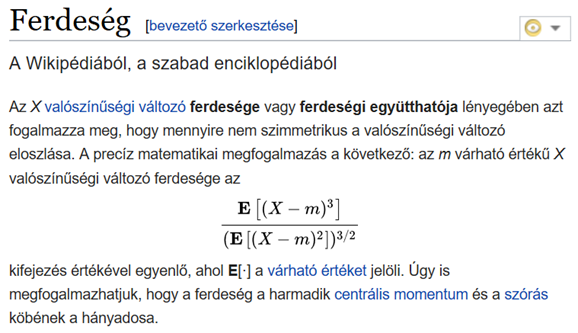
forrás: https://hu.wikipedia.org/wiki/Ferdeség

Nekem ez az a pont, amit nemhogy nem értek, de nem is akarom érteni, mert nem érzem, hogy milyen gyakorlati haszna lenne ennek az ismeretnek a számomra (talán egyszer majd megpróbálom értelmezni a dolgot, de nem most). Az excel és a statisztikai szoftverek is ezzel a csodálatos képlettel (vagy valamelyik másik hasonlóan bonyolulttal) számolnak, igazából az a fontos, hogy hogyan értelmezzem az eredményeket. A ferdeségi együttható esetében az a fontos, hogy

- ha az értéke 0, akkor a sűrűségfüggvény tökéletesen szimmetrikus. -0,5 és +0,5 között van, akkor a sűrűségfüggvény aszimmetriáját elfogadhatónak tekintjük.

- Ha az együttható értéke -0,5-nél kisebb, de -1-nél nagyobb, illetve 0,5-nél nagyobb, de 1-nél kisebb, akkor a sűrűségfüggvény aszimmetriája közepes mértékű.

- Ha az együttható értéke -1-nél kisebb, illetve 1-nél nagyobb, akkor a sűrűségfüggvény erősen aszimmetrikus.

Az első esetben a ferdeségi együttható értéke igazolja, hogy az adatsor lehet normál eloszlású, a második és a harmadik esetben ezt nagy valószínűséggel kizárnám. Emlékeztetőül újra ide másolom a korábbi cikkben alkalmazott ábrát a sűrűségfüggvény ferdeségéről:

Ennek megfelelően, ha a ferdeségi együttható értéke pozitív (lásd a jobbszélső ábrát, ahol a mean, azaz az átlag nagyobb, mint a medián és a módusz), akkor azt mondjuk, hogy a sűrűségfüggvénynek ferdesége van jobbra. Ha a ferdeségi együttható értéke negatív, az azt jelenti, hogy a sűrűségfüggvénynek ferdesége van balra. Ha ránézek, nekem pont fordítva lenne logikus az elnevezés, mert úgy érzem, hogy a baloldali görbe jobbra dől, a jobboldali meg balra. Mindegy, igazából az a fontos, hogy értsük, hogy kb. milyen a görbe alakja a ferdeségi együttható értékének függvényében.

Ha nincs szoftverem, tehát valamit ténylegesen ki is kell számolnom, akkor szívem szerint nem ezt a ferdeségi együtthatót használnám, hanem maradnék a már korábban ismertetett quartilisek alapján kiszámolható ferdeségi együtthatót alkalmaznám, illetve létezik kér egyszerű együttható, amik még ennél is egyszerűbbek: A Pearson-féle ferdeségi együtthatók (Person’s coefficient for skewness):

Pearson-féle ferdeségi együttható I:

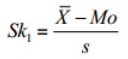tehát az átlagból kivonjuk a móduszt és ezt a különbséget elosztjuk a szórással.

Pearson-féle ferdeségi együttható II:

tehát az átlagból kivonjuk a mediánt, a különbséget megszorozzuk hárommal és ezt osztjuk el a szórással.

Mivel egy korábbi leckében (itt) már megtanultuk, hogy a kieső értékek erősen befolyásolják az átlagot, már egy-két – az átlagtól távolabb eső - érték is befolyásolni fogja a fenti együtthatók értékeit.

Most nézzük meg, hogy a korábban használt adatsor esetében hogyan működnek a ferdeségi együtthatók:

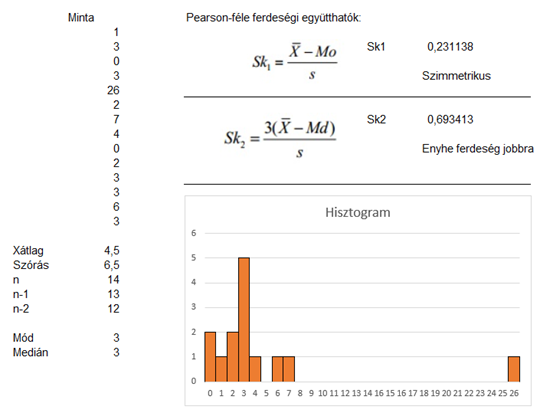Amint azt már korábban megtudtuk, az adatsorunk esetében a medián és a mód megegyezik, az átlag viszont jelentősen eltér ezektől. Ennek megfelelően biztos, hogy a ferdeségi együtthatók közül egyik sem lesz nulla. Pont az előbbiek miatt a mediánnal számolt együttható pont háromszor akkora, mint a módusszal számolt, tehát ez esetben ez érzékenyebb. Egy más adatsor esetében kaphatunk teljesen más eredményt is. Viszont most nézzük meg, mi történik akkor, ha eltávolítjuk az egy kieső adatunkat:

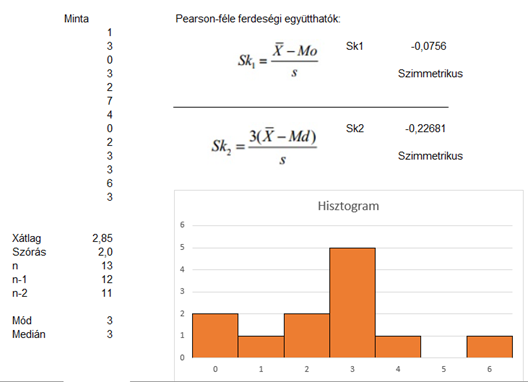
Ez esetben mindkét ferdeségi együttható értéke jelentősen csökkent, hiszen az átlag távolsága a mediántól és a módusztól is jelentősen csökkent.

1.       Lapultság (kurtosis)

Ez a mérőszám hasonlóan „egyszerű”, azt mutatja meg, hogy az adatsorunk sűrűségfüggvénye magasabb vagy lapultabb, mint a normál eloszlás sűrűségfüggvénye. Ez esetben a normál eloszlásnak abból a tulajdonságából indulunk ki, hogy az átlag körüli ±3-szoros szórás tartományában várható az elemek 99,73%-a. Ha a mi adatsorunk is normál eloszlást mutat, akkor hasonló tulajdonságokat várunk tőle. A lapultság „hivatalos” meghatározása itt is kacifántos:

forrás: https://hu.wikipedia.org/wiki/Lapultság

A statisztikai szoftverek ezt a módszert alkalmazzák, itt sem kell foglalkoznunk azzal, hogy a program mit számol, csak az eredmények értelmezésére kell ügyelnünk. A fenti képletben azért vonnak ki a tört értékéből hármat, hogy ugyanúgy lehessen értelmezni, mint a ferdeségi együtthatót, tehát a 0 az optimális érték és a pozitív, illetve a negatív értékek jelölik a sűrűség görbe csúcsosságát vagy lapultságát. Érdemes ellenőrizni az alkalmazott statisztikai szoftver leírásában, hogy a nulla vagy a három jelenti az optimális állapotot. Az R például többféle lapultsági együtthatót is képes alkalmazni, a függvény paraméterei között kell megadni, hogy melyik képlettel számoljon a program. A Minitab a fent említett képletet alkalmazza, amelynél az optimális állapot esetében 0 az együttható értéke.

Szerencsére itt is van egyszerűbb megoldás a problémára, ami könnyebben érthető, ezt Moors-féle lapultsági együtthatónak hívják és hasonlóan a Bowley-féle ferdeségi együtthatóhoz, itt is egyenlő részekre kell felosztani a sűrűség görbe tartományát. A módszer alapgondolata az, hogy az adatok nagy többsége az átlag ± 1xszórás tartományban lesz. Ez esetben viszont nem négy, hanem hat egyenlő részre kell osztani a tartományt a következő módon:

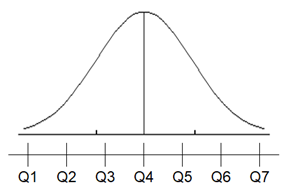
Egyeseknek ismerős lehet ez a kép, hiszen a képen mintha a ±1, ±2 és a ±3-szoros szórástartományt látnánk a képen. A Moors-féle lapultsági együttható képlete a következő:

1,23-at azért kell kivonni a képletből, mert így biztosítható ugyanaz a döntési mechanizmus, ami a hasonló együtthatók esetében, tehát akkor lesz nulla az eredmény, ha az adatsor magassága pontosan megegyezik a tökéletes normál eloszlás magasságával.

Szokásom szerint kipróbáltam, hogyan működik a képlet különböző adatsorokra. Először generáltam 50-elemű normál eloszlású mintákat különféle szórásokkal, majd generáltam egy T-eloszlású adatsort is. Itt láthatók a mintás sűrűség görbéi (sajnos nem lettek túl szépek), de az jól látható rajtuk, hogy a normál eloszlású görbék esetében a középpont körül és a széleken lévő adatok aránya kb. egyforma. A T-eloszlás görbéje sokkal „vékonyabb”, tehát itt más eredményt várunk:

És akkor lássuk, hogy milyen eredmények jöttek ki a Moors-féle lapultsági együtthatóra:

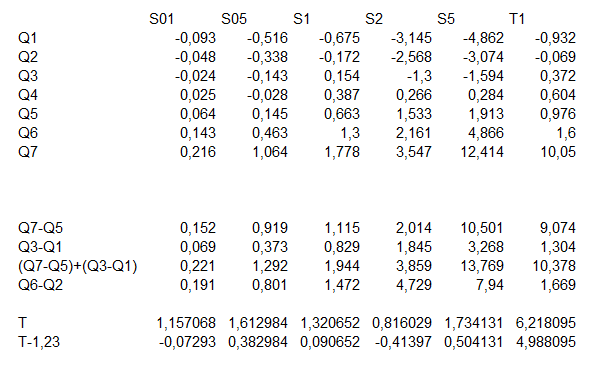
Az eredmények jól mutatják, hogy amíg a normál eloszlású adatsorok esetében a ’T-1,23’ értéke végig -0,5 és +0,5 között van (még a bimodális, tehát két csúccsal rendelkező adatsor esetében is), addig a T-eloszlású adatsor esetében 5 körüli értéket kaptam, ami messze kívül esik a megfelelőségi tartományon.

Összefoglalás:

Sikerült egy eléggé bonyolult témába belenyúlni, hiszen a ferdeség és a lapultság alkalmazását már nem olyan egyszerű elmagyarázni, mint a középérték és a szóródás mérőszámok alapelveit. Szerencsére sikerült mindkét esetben találni olyan egyszerű és jól érthető ferdeségi és lapultsági együtthatókat, amelyeket kis odafigyeléssel meg lehet érteni és ha kevés eszközünk áll rendelkezésre, akár kézzel vagy táblázatkezelővel is ki tudjuk őket számolni. A „hivatalos” együtthatók értelmezésére most nem vállalkoztam, mert úgy érzem, hogy ezzel túllépnék a saját magam által kijelölt kereteken, de talán sikerült ezek értelmezését, illetve gyakorlati alkalmazását is bemutatni. A gyakorlati példák segítségével szerettem volna megvilágítani, hogy ezek az együtthatók szigorú követelményt jelentenek annak eldöntésében, hogy az adatsor normál eloszlású-e vagy sem. Remélem sikerült!

Irodalom:

Tae Hwan Kim – Halbert White: One more robust estimation of skewness and kurtosis: Simulation and application ont he S&P500 index, September 2003 - https://cirano.qc.ca/realisations/grandes_conferences/methodes_econometriques/white.pdf

Moors, J.J.A: A quantile alternative for kurtosis - https://pure.uvt.nl/ws/portalfiles/portal/1177381/MJ5616058.pdf