Most vissza szeretnék térni egy régebben tárgyalt témára, mert igazából egy kicsit befejezetlen maradt (az előző bejegyzést lásd itt).

Ott hagytam abba a történetet, hogy a variancia négyzetgyöke, azaz a szórás normál eloszlású adatok esetén átlagosan 15-30%-al magasabb értéket ad, mint az átlagtól való eltérések abszolút értéke. Ez persze így szépen hangzik, de a kíváncsiságom megint nem hagyott nyugodni. Már az előző bejegyzés megírásakor megpróbálkoztam azzal, hogy – szokásomhoz híven – modellezzem az eredményeket. Ehhez megpróbáltam a lehető legegyszerűbb esetet alkalmazni: azt, amikor egy kételemű adatsor szórását számolom ki. A választásomat erősen befolyásolta az a tény, hogy a kételemű adatsor szórása egy kétváltozós függvényként értelmezhető egy megadott tartományban, amely viszont a háromdimenziós térben még ábrázolható.

Excelben ezt nem sikerült elegánsan megoldani, ezért az R-t és az RStudio-t hívtam segítségül. Itt készítettem két x változót (x1 és x2), majd elkészítettem a két függvényt.

A kétféle számításhoz a következő képleteket használtam:

Átlagtól való eltérés abszolút értéke (MAD):

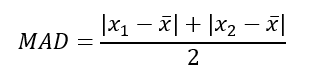
Szórás (SD):

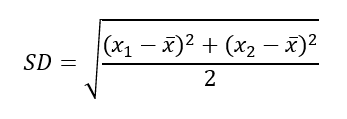
Ezután ábrázoltam a két függvényt külön-külön…

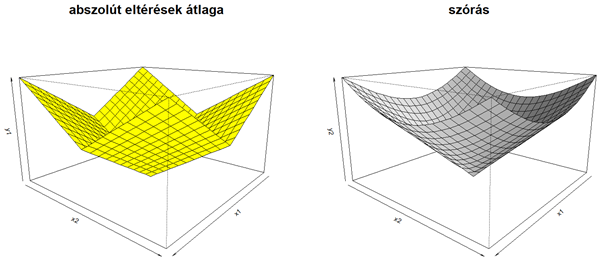
… és egymásra fektetve is:

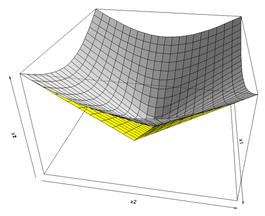
A két grafikonon jól látszik, hogy a két függvény alakja jelentősen eltér egymástól. Az eltérések abszolút értékeinek átlaga inkább egy gúlához, a szórás diagramja inkább kúphoz hasonló. De a lényeg akkor látszik, ha a két függvényt egymásra helyezzük. Vannak olyan területek, ahol a két függvény értéke megegyezik, de vannak olyan helyek, ahol viszont a szórás lényegesen magasabb értéket ad, mint az eltérések abszolút értékeinek átlaga.