Miután ilyen szerencsésen megismerkedtünk a kétmintás t-próbával (Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba), tehát az eddigi gyakorlatnak megfelelően vezessük le táblázatkezelőben és Minitab-ban is az előző cikkben említett feladatot.

Noha ebben az esetben már egy kicsit több átalakításra van szükség az egymintás t-próbához képest, azért még ez sem annyira bonyolult, hogy ne lehetne követni. A következő feladatokat kell elvégeznünk az átalakítás során.

• Eddig csak egy mintával dolgoztunk, de mostantól két mintánk van, tehát be kell szúrnunk egy oszlopot a második mintának.
• A sokaság átlagát ki kell törölni, és a minta jellemzőit át kell alakítani úgy, hogy mindkét minta jellemzői kiszámításra kerüljenek
• ’t’ értékének képletét meg kell változtatni a kétmintás t-próba számítási módjának megfelelően
• A Student t-eloszlás határértékeinek kiszámításához meg kell változtatni a T.INVERZ() függvényben a szabadsági fokok számát
• A megbízhatósági intervallumok kiszámításakor szintén meg kell változtatni a képleteket a kétmintás t-próbának megfelelően

Akkor lássunk neki!

Először is eltüntettem a sokaság átlagát és a ’t’-érték kiszámításához alkalmazott képletet, hogy ne zavarjon. Ezután beszúrtam egy új oszlopot a második minta (Minta2) értékeinek, illetve a minta adatai helyett mindkét minta átlagát, szórását és mintaszámát ki kell számolni, ezért az ehhez szükséges mezőket is elhelyeztem a táblában. Az első mintához hasonlóan a második minta esetében is 30 értéket tudunk megadni, amely szükség esetén tetszőleges mértékben bővíthető, csak az átlag, a szórás és a mintaszám képleteit kell megváltoztatni.

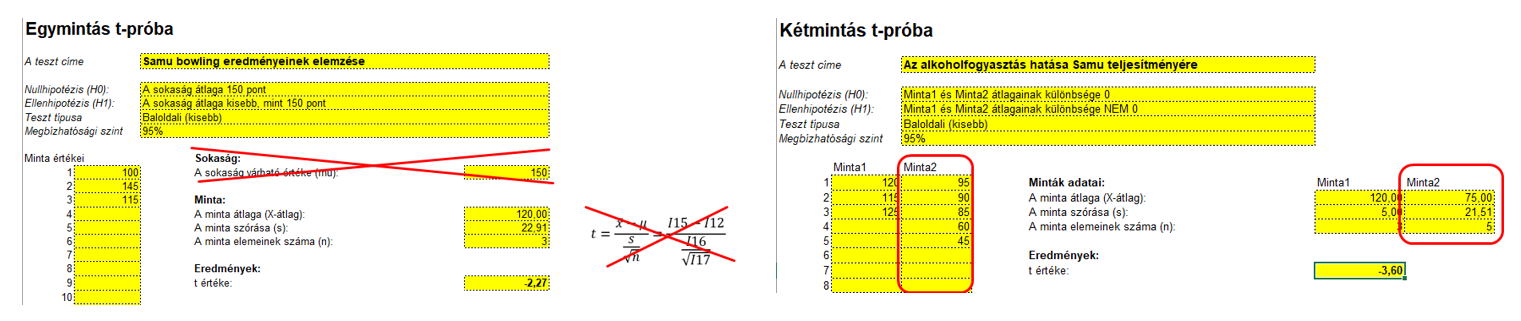
Ezután átírtam ’t’ értékének képletét a kétmintás t-próbának megfelelően.

Ezután kijavítottam a szabadsági fokok számát a Student t-eloszlás határtértékeinek képleteiben.

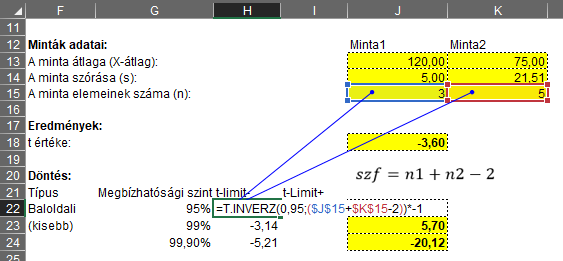
Majd a megbízhatósági intervallum határértékeinek képletét is módosítottam a már korábban leírtak szerint.

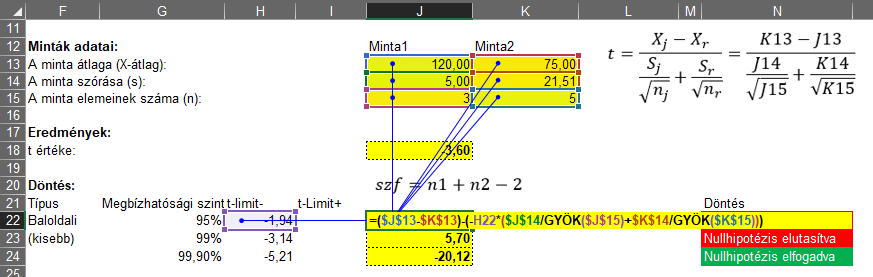
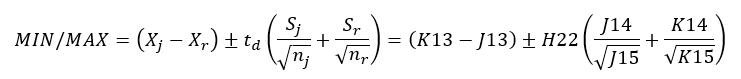
Így most már a kétmintás t-próba táblázat is működik, a végeredmény a következő lett. Látható, hogy ha a baloldali tesztet hajtom végre, akkor 99,9%-os megbízhatósági szint esetében el tudom fogadni a nullhipotézist azaz, ha nagyon-nagyon óvatos vagyok, akkor nem mondhatom, hogy Samu teljesítményét rontja az alkohol. Ha kétoldali tesztet végzek, akkor viszont már 99%-os megbízhatósági szinten sem lehetek biztos a fenti állítás igazságában.

 Az eredmények visszaellenőrzése érdekében elvégeztem a számítást a Minitab program segítségével is és a következő eredményeket kaptam.

Először is átmásoltam a minták adatait Minitab-ba.

Ezután előhívtam a kétmintás t-próba menüpontot.

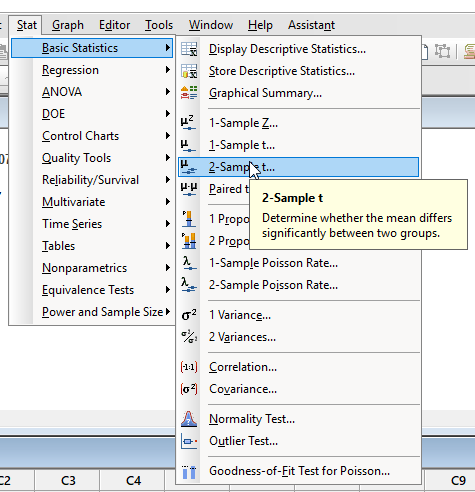
Itt most be kellett állítani, hogy a minták adatai egy oszlopban vannak és egy másik oszlop adatai alapján lehet őket csoportosítani, vagy a két minta adatai két különböző oszlopban vannak. Mivel a második eset az igaz, ezért így állítottam be az adatbevitelt.

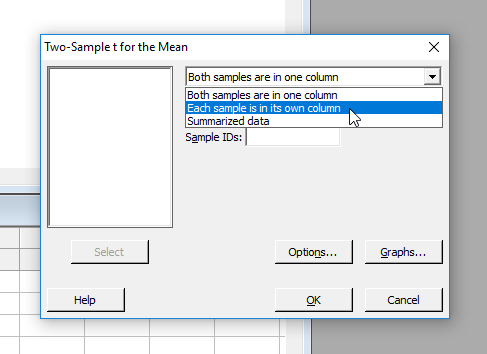
Ezután megadtam a két minta adatait tartalmazó oszlopokat.

Az ’Options’ gomb megnyomásával eljutottam ahhoz az ablakhoz, ahol a teszt típusát és megbízhatósági szintjét lehet beállítani, majd itt is beállítottam a kívánt feltételeket. A megbízhatósági szint 95%, a nullhipotézisünk alapján a két minta átlaga közötti különbség 0. A Minitab-ban van egy olyan opció is, hogy meg lehet adni egy minimális vagy maximális különbséget a két mintaátlag között, adott esetben ez hasznos lehet. Az alternatív hipotézis esetünkben az, hogy a két mintaátlag különbsége nagyobb, mint 0 hiszen kisebb nem lehet. Jelen esetben nem jelöltem be azt, hogy feltételezzük, hogy a két minta varianciája (szórásának négyzete) megegyezik, hiszen tudom, hogy a két variancia nem egyezik meg.

Ezután a ’Graphs’ gomb megnyomásával előhívtam egy másik ablakot, ahol kértem, hogy a két minta grafikus ábrázolására jelenítsen meg a Minitab egy boxplot diagramot.

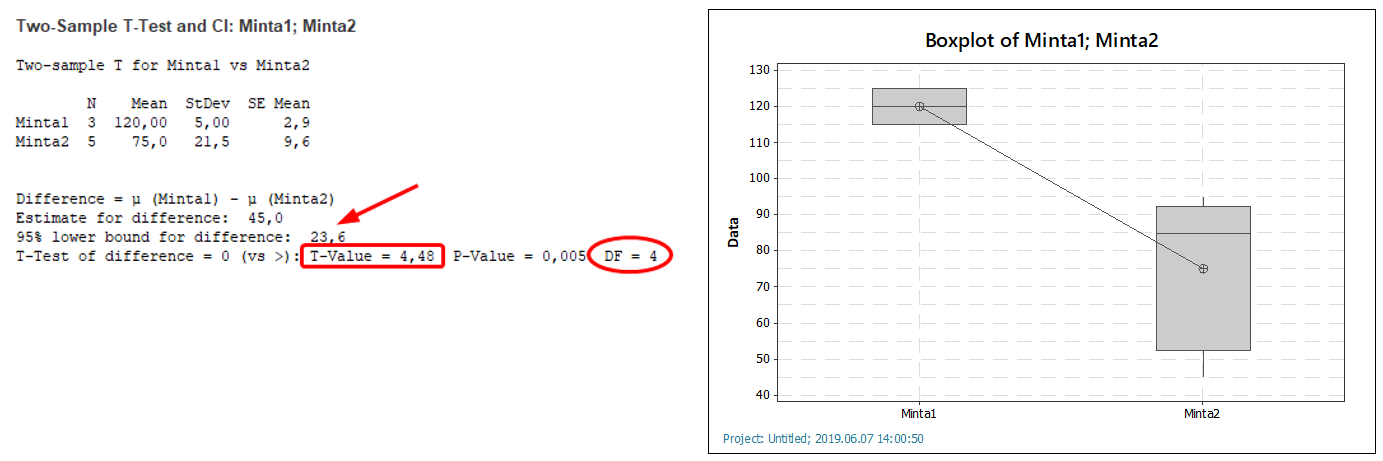
Most először viszont az fordult elő, hogy a táblázatkezelő és a Minitab nem ugyanazt az eredményt hozta ki. A megbízhatósági intervallum alsó határa a táblázatkezelőben 20,7 volt, míg a Minitab 23,6-ot számolt. ’t’ értékére a táblázatkezelő -3,6-ot adott, míg a Minitab 4,48-at. Érdekes módon a szabadsági fokok száma a táblázatkezelőben 6 volt, míg a Minitab 4-et adott. De mit jelenthet ez a különbség. Szerencsére a google gyorsan talált egy weboldalt, ahol megtalálhatók a Minitab által alkalmazott képletek, amely azonnal megadta a különbségek okát:

Látható, hogy a Minitab ez esetben egy kicsit más képleteket használ, mint amelyeket én használtam, így az ő eredménye egy kicsivel szigorúbb lett annál, amit én számoltam ki.

Végül álljon itt a teszt végeredménye: