Ott tartottunk, hogy összehasonlítottuk két egymástól független minta átlagát, vajon megegyeznek-e (Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba). Noha még itt is lehetne elmélkedni egy csomó dologról, például arról, hogy másképpen számoljuk ki ’t’ értékét, ha feltételezzük, hogy a két minta szórása megegyezik, vagy hogy miért számolja a Minitab a szabadsági fokok számát azzal a bonyolult képlettel (Kétmintás t-próba táblázatkezelőben), de most inkább hagyjuk Samut pihenni a sok bowlingozás után.

Sok érdekes példát lehetne hozni a páros t-próbára például egy fogyókúrás módszer hatékonyságának elemzésére, ahol megmérjük a fogyókúrázók tömegét a fogyókúra előtt és után, majd összehasonlítjuk az eredményeket, illetve egy acélból készült késpenge edzésének elemzése, ahol kíváncsiak vagyunk rá, hogy a penge keményebb lett-e az edzés után, mint előtte volt. A lényeg az, hogy amikor páros t-próbát alkalmazunk, akkor a két minta elemeit ugyanonnan származtatjuk. A minták elemeit összekötik azok a dolgok, amikből származnak, a fogyókúra esetében a fogyókúrázók személye, az edzett késpengék esetében a beszámozott mintadarabok. A páros t-próba esetében a két minta elemeit mindig hozzákötjük az adatok forrásához, tehát a fogyókúrázók nevéhez, vagy a késpengék sorszámához.

Tegyük fel, hogy egy gyárban dolgozunk, éppen egy bizonyos terméket gyártunk. Meg akarjuk mérni a gyártott termékek hosszát és van hozzá kétfajta mérési eljárásunk. Megmérhetjük a darab hosszát mikrométerrel, vagy egy mérőórás magasságmérő asztalon. Az első esetben egyszerűen megmérjük a mikrométerrel a darab hosszát. A második esetben mérőhasábokból összeállítjuk a darab hosszméretének névleges értékét, ehhez lenullázzuk a mérőórát, majd a darabot a mérőóra alá helyezve leolvassuk az óráról a darab eltérését a névleges mérethez képest. Kíváncsiak vagyunk rá, hogy a két mérőeszköz egyforma eredményt ad, vagy sem.

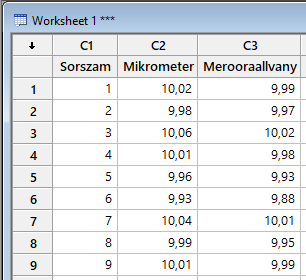
A kísérlet érdekében kivettünk 9 darab mintát a gyártásból és megszámoztuk őket egytől tízig, majd megmértük mind a 9 darabot mindkét mérőeszközzel. Természetesen a kétféle mérés átlagát kétmintás t-próba segítségével is össze tudnánk hasonlítani. Viszont itt van egy előnyünk, ami nagymértékben leegyszerűsíti az életünket, mégpedig az, hogy a kétféle mérési eredményt minden egyes darabnál összeköti a mért darab sorszáma. A kísérletünk során a következő eredményeket kaptuk:

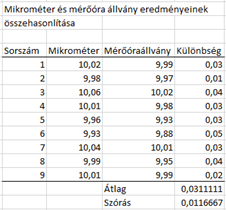
A Sorszám oszlopban az egyes munkadarabok sorszáma szerepel, a Mikrométer és a Mérőóraállvány oszlopokban pedig a kapott mérési eredmények. Végül a különbség oszlopban a munkadarabokhoz tartozó kétféle mérési eredmény különbsége látható. Ezt egyszerűen megtehetjük, hiszen a munkadarabok erős kötelékkel kötik össze a kétféle mérés eredményeit. Innentől pedig már egyszerű a dolgunk, hiszen csak azt kell vizsgálnunk, hogy a 'Különbség' oszlop vajon lehet-e nulla, vagy sem. Ehhez viszont már elő tudjuk venni öreg barátunkat, az egymintás t-próbát (Z helyett t – leheletnyi különbség), ’t’ kiszámításához csak annyit kell módosítanunk rajta, hogy a sokaság átlaga helyére nullát írunk:

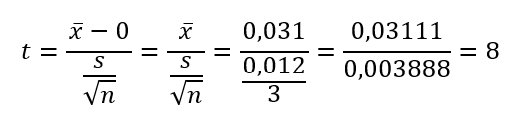
Ha mindezt excelben is végig számoljuk, akkor a következőket kapjuk:

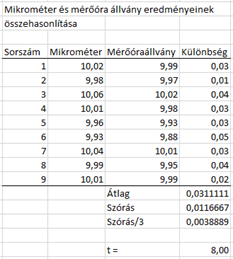
Az eddigi rutinunk alapján már talán érezhető, hogy ’t’ értéke igen magas, tehát már akár számíthatunk is rá, hogy a két mérőrendszer nem egyforma eredményt ad, de a rend kedvéért nézzük meg, hogy mennyi a döntési határérték.

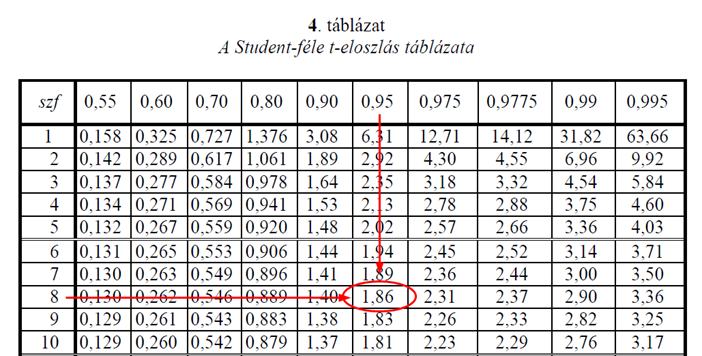
Az n-1-hez, azaz 8-hoz és 95%-os megbízhatósági szinthez tartozó t-határérték 1,86. Ez jelentősen kisebb, mint a próba statisztika által adott t = 8 érték, ezért a nullhipotézist, azaz azt, hogy a két mérőrendszer eredményeinek átlaga lehet 0, elutasítom.

Most pedig nézzük meg, hogy milye eredményt ad erre a Minitab. Először is átmásoltam a kapott mérési eredményeket a Minitab-ba.

Ezután elindítottam a páros t-próbát.

Mivel az eredmények külön oszlopokban vannak, ezért a felugró ablakban ezt változatlanul hagytam.

A két mintának kiválasztottam az előzőleg bemásolt két oszlopot.

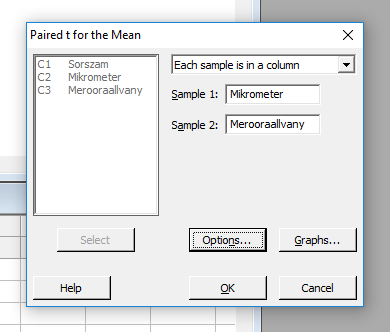
Az Options gomb megnyomásával előugró másik ablakban beállítottam a hipotézisvizsgálat megbízhatósági szintjét (0,95) és aéternatív hipotézisként (H1), hogy a különbség nagyobb, mint 0.

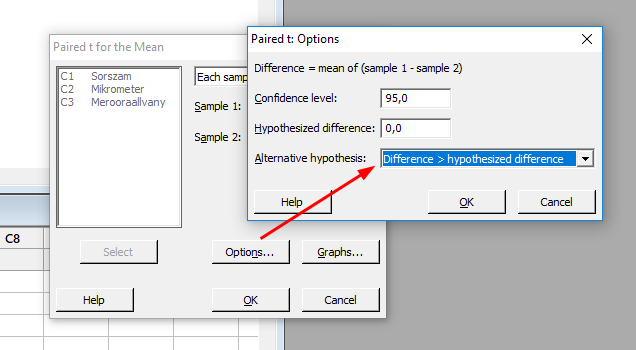
A kapott eredmények ebben az esetben aránylag jól értelmezhetők.

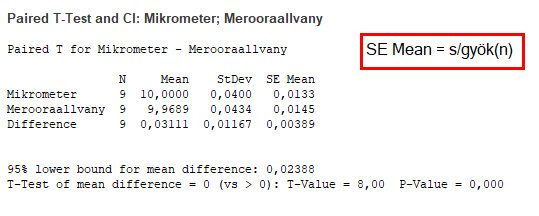
A vizsgálati cél megadása után következő táblázat tartalmazza az adatok alap statisztikáit, 'N' mutatja a mintaszámot, a 'Mean' jelenti az átlagot, az 'StDev' jelenti a szórást, az 'SE Mean' oszlop pedig az átlag standard hibáját tartalmazza (Az átlag standard hibája). A 95% lower bound ismét csak úgy jön ki, hogy a ’t’ értékének kiszámításához használt képletbe behelyettesítjük a t-eloszlás táblázatból kapott 1,86-ot, majd kifejezzük a két minta átlagának különbségét.

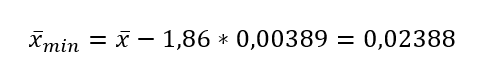
Ez a két mérési sor különbségének az a legkisebb értéke, amit még felvehetne úgy, hogy a nullhipotézist elfogadjuk. Viszont ez az érték nagyobb, mint 0, így a nullhipotézist mindenképpen el kell vetnünk, tehát a két mérőeszköz nem ugyanazt a mérési eredményt adja a munkadarabok mérésekor.