
Egy korábbi bejegyzésben már bemutattam (Roulette a la Monte Carlo, avagy csaltak vagy nem csaltak...?), hogy Karl Pearson matematikus az 1890-es években sokat foglalkozott a rulettel és azzal, hogy vajon a monacói kaszinók rulettkerekei mennyire működnek véletlenszerűen. Úgy döntöttem, hogy megvizsgálom egy kicsit részletesebben, hogy mi is volt a híres matematikus problémája és egyben megragadom az alkalmat az illeszkedés vizsgálatára alkalmazott khí-négyzet próba bemutatására.
Pearson problémája a következő volt:
„… Következőként (Pearson) azt vizsgálta meg, hogy átlagosan hányszor lett egymás után piros vagy fekete az eredmény. Amikor összehasonlította azt, hogy hányszor nyert egymás után kétszer, háromszor, négyszer vagy többször a piros, vagy a fekete azokkal a gyakoriságokkal, amelyeket akkor kellett volna kapnia, ha a rulettkerekek működését csak a véletlen befolyásolja, azt tapasztalta, hogy valami nem stimmelt. Az egyes sorozatok sokkal ritkábban fordultak elő, mint az várható lett volna és az, amikor a színek váltogatták egymást - például két fekete között volt egy piros vagy két piros között volt egy fekete – sokkal gyakrabban, mint kellett volna. …”
Szerencsére megtaláltam az eredeti táblázatot, amelyben Pearson összefoglalta az eredményeit:
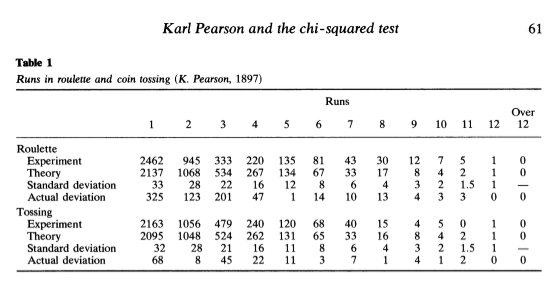
forrás: https://pdfs.semanticscholar.org/8d94/835a2f49607c22a081741a59a502a24d4e43.pdf
R.L. Plackett: Karl Pearson and the Chi-squared Test, International Statistical Review, 51 (1983), pp. 59-72. Longman Group Limited
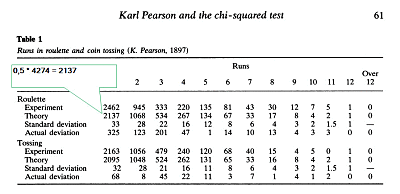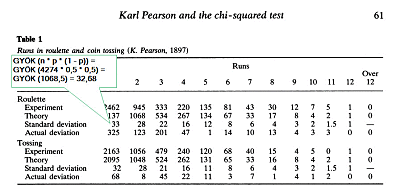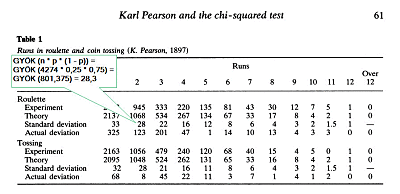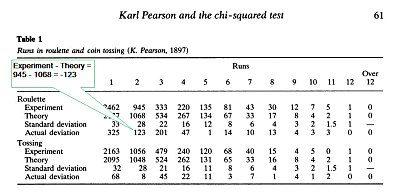
A táblázat első ránézésre nem mond túl sokat, egy kicsit értelmezni kell ahhoz, hogy megértsük, mit is tartalmaz valójában a fenti táblázat. Az tiszta, hogy a táblázat két részből áll. Először a rulett eredmények (Roulette), utána pedig a Pearson és segédje által elvégzett érme feldobások eredményei (Tossing vagy coin tossing) vannak összegezve. Az oszlopok fejlécében lévő számok egytől tizenkettőig azt jelölik, hogy hányszor fordult elő ugyanaz a szín (piros vagy fekete) a rulettben, illetve érme oldal (fej vagy írás) egymás után. A sorok fejlécében több kifejezés is magyarázatra szorul. A magyarázat egyszerűsítése érdekében csak a rulett eredmények segítségével magyarázom majd az egyes sorok jelentését, de az érme feldobásokra ugyanaz vonatkozik.
- Az ’Experiment’ sor tartalmazza azt, hogy a vizsgálatok során ténylegesen hányszor fordult elő, hogy a piros vagy a fekete szín n-szer (1, 2, 3, … ,12) jött ki egymás után megszakítás nélkül.
- A ’Theory’ sor tartalmazza azt, hogy a rulettkerék felépítése alapján ELMÉLETILEG hányszor KELLETT VOLNA előfordulnia, hogy a piros vagy a fekete szín n-szer (1, 2, 3, … ,12) jött ki egymás után megszakítás nélkül. A rulettkeréken összesen 38 zseb van, ahová a golyó beleeshet a pörgetés végén. Pearson feltételezte, hogy a 38 zsebet ugyanannyi piros és fekete szám jelöli, azaz 19 piros és 19 fekete szám van a keréken. Ez a valóságban nem így van, mert van legalább egy zöld színű mező is, amely 0-val van jelölve, ilyenkor a bank nyer. Ettől most tekintsünk el, vegyük alapnak Pearson feltételezését, különben a táblázatom nem fog megegyezni az eredeti táblázattal. Tehát az első oszlopban az a mennyiség szerepel, ahányszor a piros után egyből fekete vagy a fekete után egyből piros jött ki. Pearson feltételezése alapján a piros vagy a fekete eredmény valószínűsége 50%, azaz 0,5. Ha Pearson összesen 4274 ruletteredményt vizsgált meg, akkor a tudós azt várta, hogy az esetek felében, azaz 2137 esetben fog egyszer kijönni a piros vagy a fekete szín. Abban az esetben, ha azt várta, hogy kétszer fog egymás után kijönni a piros vagy a fekete, a valószínűség 0,5 * 0,5 = 0,25, azaz ez az összes eset negyedében fog előfordulni.
- A ’Standard deviation’ sorban a várható érték (’Theory’) szórása szerepel. Az adatoknak ez a felépítése ismerős lehet egy korábbi bejegyzésből (A binomiális eloszlás – lépjünk szintet az érmedobálásban), ott is azt vizsgáltuk, hogy mekkora a valószínűsége annak, ha az érme feldobások esetén mekkora a valószínűsége bizonyos kombinációk kialakulásának. Vagyis a vizsgált probléma esetében az adatok szintén binomiális eloszlást követnek. Ennek szórását pedig a következő módon számítjuk ki:
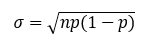
Az első oszlop esetében ez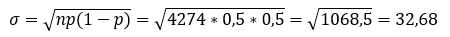
A második oszlop esetében pedig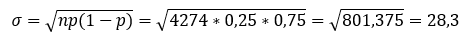
- Végül az ’Actual deviation sor’ egész egyszerűen az ’Experiment’ és a ’Theory’ értékeinek a különbségét tartalmazza.
Úgy döntöttem, hogy jobban megértsem Pearson felháborodásának okait, az illeszkedést vizsgáló Khí-négyzet próba (Chi Squares Goodness-of-fit test) segítségével kiszámolom, hogy mennyire felelnek meg a rulettkerekek és az érmedobások eredményei esetében a valóságban kapott egyszeres, kétszeres … n-szeres gyakoriságok mennyire felelnek meg az elméletben kiszámolt gyakoriságoknak. A teszt ismételten nagyon hasonlít a már korábban ismertetett hipotézis vizsgálatokhoz, itt is kiszámolunk egy – az adatsorra jellemző – khí-négyzet értéket, majd ezt összehasonlítjuk egy khí-négyzet határértékkel és az összehasonlítás eredménye alapján döntést hozunk a teszt eredményéről.
Mielőtt belekezdek a teszt elvégzésébe, ellenőriznem kell néhány kiinduló feltételt:
- A mintákat egyszerű véletlenszerű mintavétellel választottam-e ki. Ez esetben feltételezem, hogy igen, noha ismerem a tesztadatok összegyűjtésének történetét.
- A teszt változó kategória változó. Ez is igaz, hiszen összesen 12-féle csoportba tudtam osztani az adatokat a sorozatok hosszától függően, ez véges számú különféle kategóriát jelent. Ha nem vagy tisztában azzal, hogy mit jelent a kategória változó, akkor kérlek olvasd el a következő bejegyzést (A gömbölyűség mértékegysége - Az adattípusokról és mérési skálákról).
- Minden egyes kategóriában legyen legalább 5 darab megfigyelés, ez a mi adatsorunkban az egytől a tizenegy elemű sorozatokig igaz. Tizenkét elemű sorozat csak egyszer fordult elő, de most úgy döntöttem, hogy emiatt a feltétel miatt nem zárom ki a tizenkét elemű sorozatot a tesztből.
Akkor most határozzuk meg a nullhipotézist. Alapból azt feltételezem, hogy a rulettkerekek viselkedése megfelel az elméletnek, azaz a különböző hosszúságú sorozatok gyakoriságai megfelelnek az elméletileg kiszámított gyakorisági értékeknek. A kérdés tulajdonképpen az, hogy a tapasztalati és az elméleti gyakorisági értékek között tapasztalt eltérések mértéke eléri-e azt a szintet, ahol már valamilyen eltérésre gyanakszunk, vagy még nem. Természetesen az ellenhipotézisünk ennek az ellentéte, azaz a tapasztalt gyakoriságok NEM FELELNEK MEG az elméletileg kiszámított gyakoriságoknak.
H0 : A tapasztalati adatok megfelelnek az elméleti gyakoriságoknak
H1: A tapasztalati adatok nem felelnek meg az elméleti gyakoriságoknak
Az elemzés elvégzéséhez bevittem Pearson táblázatát egy táblázatkezelőbe és végig számoltam az egyes cellák értékeit, hogy leellenőrizzem az adatok helyességét. Ezt kaptam:
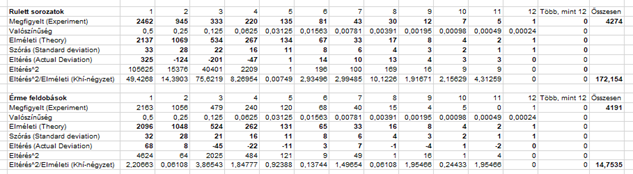
Szépen ki is jött az összes eredmény az eredeti táblázatnak megfelelően. A jobb követhetőség kedvéért mindkét esetben hozzáadtam egy ’Valószínűség’ sort, itt szerepelnek a különböző hosszúságú sorozatok elméleti valószínűségei, az ’Elméleti (Theory)’ sorokban pedig az, hogy ugyanennyi kísérlet esetében hány esetben KELLETT VOLNA kijönnie az adott hosszúságú sorozatnak. Az ’Eltérés^2’ és az ’Eltérés^2/Elméleti (Khí-négyzet)’ sorok a teszthez alkalmazott Khí-négyzet érték kiszámításához szükségesek, ugyanis a teszt statisztika k darab kategória esetében a következő:
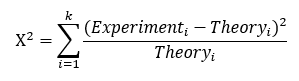
A teszt statisztika képlete alapján már nyilvánvaló, hogy az ’Eltérés^2’ sor tartalmazza minden egyes sorozatra a teszt statisztika számlálóját, az ’Eltérés^2/Elméleti (Khí-négyzet)’ sor pedig 1-től k-ig a tört értékét. Mind a rulett sorozatok, mind pedig az érmedobások esetében az utolsó sor végén található Khí-négyzet értéke, amely egyszerűen az utolsó sorban lévő elemek összege.
Viszont mielőtt folytatjuk a teszt végrehajtását, mélyedjünk el egy kicsit a teszt statisztika képletének értelmezésében, mert ez elsőre talán nem egyértelmű. A Khí-négyzet eloszlás esetében azt állítottuk, hogy a standard normál eloszlásból kivett n-elemű minta szórása n-1 szabadsági fokú khí-négyzet eloszlást követ (Khí-négyzet eloszlás – Na, már megint egy újabb eloszlás!). A most használt képlet igencsak hasonlít a fenti cikkben szereplő variancia képletre, de nem egészen ugyanaz!
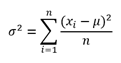
De a most alkalmazott képletben miért nem n van a nevezőben és miért az elméleti várható érték?
Ennek a magyarázata egy kicsit bonyolultabb. A tört számlálójának célja tulajdonképpen ugyanaz, megadja az egyes kategóriákban az „átlagtól” való eltérés négyzetét. A nevező pedig arra szolgál, hogy a különféle adatsorok összevethetők legyenek. Az elméleti értékektől való eltérés egy abszolút szám, emiatt az eltérések mértéke különböző mértékűek lehetnek, így ezek nem összehasonlíthatók. Ha ezeket elosztjuk az elméleti értékekkel, akkor tulajdonképpen valami hasonlót csinálunk, mint amikor egy teljesen általános normál eloszlást standardizálunk, vagy amikor a korrelációs együttható esetében elosztottuk az egyes adatpontoknak az x és y irányú átlagoktól való eltérését az x és y irányú szórásokkal, hogy megkapjuk a Z-értékekben mért távolságokat (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?). Itt viszont nem normál eloszlású a várt khí-négyzet érték, hanem khí-négyzet eloszlású. Azaz ebben az esetben az elméleti értékektől való eltéréseket nem normalizáljuk, hanem inkább „khínégyzetesítjük”!
De a normalizálás képletében a nevezőben egy szórás szerepel, míg a fenti képletben – amely egy variancia képlet – a mintaszám szerepel. A zűrzavar feloldása érdekében tisztázzuk, hogy ez esetben az elméleti érték szerepe egy szórás és nem egy mintaszám, tehát ebben az esetben inkább a standardizálás képletére hasonlít az általunk használt statisztika.
De az elméleti érték miért szórás? Tulajdonképpen eloszthatnánk a különbségek négyzetét a valós megfigyelések értékével is (Experiment). Viszont ez esetben a valós megfigyelések értékei az úgynevezett Poisson-eloszlást követik (de hiányzott még egy eloszlás!), és a Poisson-eloszlás szórása megegyezik a várható értékkel, azaz az elméleti értékkel (Theory)!
Miután ezt ilyen ügyesen tisztáztuk (remélem érthető volt), fejezzük be a tesztet. A rulett sorozatok esetében kiszámítottuk a khí-négyzet értéket, amely egy igen magas szám lett (172,154). A döntéshez még hiányzik a khí-négyzet határérték, amelyet vagy khí-négyzet eloszlás táblázatból, vagy pedig táblázatkezelőben függvény segítségével tudjuk meghatározni. Ha khí-négyzet eloszlás táblázatot használunk, akkor a következőt kapjuk:
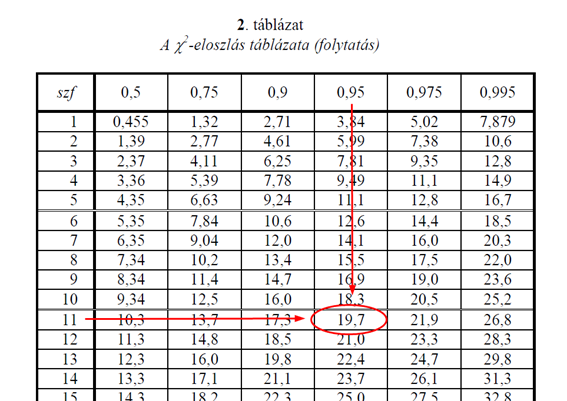
A táblázatban a 95%-os megbízhatósági szinten a 11 szabadsági fokú khí-négyzet függvény értéke 19,7. Ez szabad szemmel is jál láthatóan kisebb, mint a fenti kalkulációval kapott 172,154, azaz a döntésem az, hogy a nullhipotézist elvetem és az ellenhipotézist fogadom el, mégpedig toronymagas eredménnyel. A következtetésem az, hogy a rulett sorozatok előfordulási gyakorisága NEM FELEL MEG az elméletileg elvárt gyakoriságoknak.
A rend kedvéért végezzük el ugyanezt az ujjgyakorlatot az érmedobások esetében is. Ekkor a fenti táblázatból jól látható, hogy khí-négyzet értéke jelentősen kisebb, mint a rulett sorozatok esetében (14,7535). Ez az érték még az előbb meghatározott khí-négyzet határértéknél is kisebb (vegyük észre, hogy mindkét esetben 50% esélye van a piros vagy a fekete szín előfordulásának, illetve a fej vagy az írás előfordulásának). Ez alapján az érmefeldobások esetében el tudom fogadni a nullhipotézist, tehát az érmefeldobások esetében a valóságban tapasztalt gyakoriságok megfelelnek az elméletileg kiszámolt gyakorisági értékeknek!
Összegzés:
Fogadjuk el, hogy amikor először ránéztél Pearson eredeti táblázatára, még a történet ismeretében sem tudtad volna megállapítani, hogy a rulett sorozatok vagy az érmefeldobások megfelelnek-e az elméleti értékeknek. Az illeszkedés vizsgálatára Pearson által kitalált teszt tényleg egyértelművé teszi a fenti kérdés eldöntését és segít a megfelelő döntés meghozatalában. Végső soron megállapíthatom, hogy Pearson jogosan reklamálta a rulettkerekek működésének anomáliáit. A következő cikkben be fogom mutatni ugyanezt a varázslatot tesztet Minitab segítségével is.





