Bernoulli professzor természetesen nem elégedett meg a fenti eredményekkel (az előző bejegyzést lásd itt), tovább fejlesztette elméletét abban, az irányban, hogy mi történik akkor, ha az érménket nem egyszer, hanem n-szer dobjuk fel egymás után - azaz n számú Bernoulli kísérletet végzünk el - akkor mekkora valószínűsége annak, hogy az n számú kísérletből k alkalommal lesz fej az eredmény.

Próbaképpen vizsgáljuk meg, mi történik akkor, ha az előző érme feldobást megismételjük ötször egymás után úgy, hogy a következő eredményt kapjuk:

fej, fej, írás, fej, írás

Mi a valószínűsége annak, hogy a következő eredményt kapjuk? Mivel az érme feldobásai egymástól teljesen függetlenek, ezért

· az első fej valószínűsége p lesz,

· a másodiké megint p,

· a harmadik írás valószínűsége (1-p),

· a negyedik fej valószínűsége megint p,

· az ötödik írás valószínűsége pedig megint csak (1-p) lesz.

Mivel az öt egymástól független esemény valószínűsége megegyezik az egyedi valószínűségek szorzatával, ezért

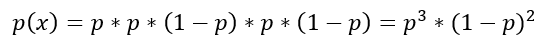
Ha a fenti példát általánosítjuk és feltesszük, hogy az érmét n-szer dobjuk fel, és ebből k alkalommal lesz fej, azaz siker az események végeredménye, akkor

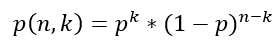
Ez az egyenlet a Bernoulli eloszlás sűrűségfüggvénye, ami a próbák száma és a próbák során kapott sikeres végeredmények alapján megadja az adott esemény előfordulási valószínűségét.

Ha ez igaz, akkor mekkora a valószínűsége annak, hogy az előző öt érme feldobásból háromszor fej lesz az eredmény?

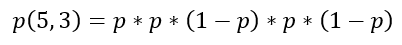
behelyettesítve p és (1 - p) értékét

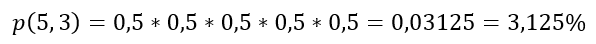
Mivel az érme feldobás esetében p és (1-p) is 50%, azaz 0,5, ez a példa nem túl szemléletes, de most már maradjunk ennél. Akkor a fentieket lefordítva, száz kísérletből, amikor ötször egymás után feldobjuk az érménket, körülbelül háromszor fog előfordulni, hogy öt kísérletből háromszor lesz fej az eredmény. Természetesen ugyanezt az eredményt kapnánk n és k értékét a Bernoulli-eloszlás sűrűségfüggvényének képletébe behelyettesítve. De igaz ez?

Mi lenne, ha kipróbálnánk a gyakorlatban is, hogyan működik az elméletünk? A példa kedvéért készítettem 100 darab 5 elemű halmazt táblázatkezelő program segítségével, amelyek véletlenszerűen csak 0-kat és 1-eseket tartalmaznak. Ezután minden ötös sorozat esetében megszámoltam, hogy hány darab 1-es és hány 0 van az egyes csoportokban. Amikor leszűrtem azokat a csoportokat, amelyekben 3 darab 1-es és 2 darab 0 volt, akkor azt kaptam, hogy a százból 34 olyan mintát találtam, amely megfelelt a fenti feltételeknek. De ez 34%-os arányt jelent a fentebb kiszámított 3,5%-al szemben, ami 3 vagy 4 csoportot jelentene. Akkor most mi történt? Az adatokat egy kicsit figyelmesebben megvizsgálva arra jutottam, hogy nem vettem figyelembe az adatok sorrendjét. A fenti képlettel csak azokat a csoportokat szűrtem ki, amelyeknél az 1-ek és a 0-k sorrendje pontosan megegyezett a kiinduló fej, fej, fej, írás, fej, írás sorrenddel. Amikor ennek megfelelően szűrtem le a mintákat, pontosan négy olyan mintát találtam, amelyben a találatok sorrendje megegyezett a kiinduló állapottal. Ez megfelel a kapott eredménynek, viszont nem ez volt a kérdés.

Tovább vizsgálva a mintákat rájöttem, hogy azokat a mintákat is figyelembe kell vennem, ahol pontosan 3 darab 1-es és 2 darab 0-s volt, de az 1-ek és a 0-k sorrendje különbözött attól, amit az elején megadtam. Rendben, de hogyan tudom kiszámítani azt, hogy hányféle sorrendben követhetik egymást az 1-ek és a 0-k, ha pontosan 3 darab 1-es van az ötelemű mintában?

Itt hivatkoznék az előző kombinatorika bejegyzésre, ahol megbeszéltük a permutáció, a kombináció és a variáció jelentését és kiszámításának módját. Ez az eset hasonlít a lottószám sorsoláshoz, ahol szintén nem számít a kihúzott számok sorrendje, tehát ez is egy kombináció. Ha tehát úgy képzeljük el, hogy hogyan tudunk öt számból hármat kiválasztani úgy, hogy a sorrend nem számít, akkor azt kapjuk, hogy ez (5 x 4 x 3) / (2 x 3) = 10. És érdekes módon, ha az eredetileg kapott 3,125%-ot megszorozzuk a kombinációk számával, azaz 10-zel, akkor körülbelül meg is kapjuk a kísérletben kapott 34%-ot. 

És itt most megint iderángatom az okos matematikusok által alkalmazott formulát, amelyet a legtöbb valószínűségszámításról szóló tankönyvben megtaláltok:

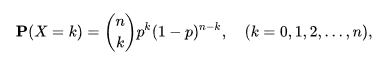
Tudom, hogy első ránézésre ez a képlet is eléggé kínainak tűnik, de remélem, hogy a fenti magyarázat alapján most már értelmezhetővé vált a jelentése.