A kéttényezős varianciaanalízist egy korábbi bejegyzésben (Most nem almára lövünk - kéttényezős varianciaanalízis (Two-way - ANOVA)) már részletesen kiveséztük, így most jöjjön a Minitab változat, amely ismételten sokkal több információt tartalmaz, mint a szimpla táblázatkezelős elemzés – nem véletlen kérnek pénzt is érte. A vizsgálathoz ugyanazt az adatsort fogom használni, hogy az eredmények összevethetők legyenek.

A Minitab korábbi verzióiban volt külön menüpont a kéttényezős varianciaanalízisre, de a 17-es változattól kezdve ezt megszüntették a szoftver készítői arra hivatkozva, hogy a 'General Linear Model' segítségével ezt a vizsgálatot ugyanúgy végre tudjuk hajtani.

Ennek megfelelően természetesen nem fogunk ’Two-way ANOVA’ menüpontot találni. Az alábbi képen látható, hogy van egy ’Balanced ANOVA’ menüpont is, és a mellette található ikon alapján helyesen tippeljük, hogy ez is kéttényezős varianciaanalízist takar. Igazából használható ez is, de arra vigyáznunk kell, hogy egyrészt ez csak „kiegyensúlyozott”, azaz „balanced” design esetén használható, vagyis minden csoportban azonos számú adat található, másrészt nem számol a tényezők közötti interakciókkal. Ha ezzel a két feltétellel együtt tudunk élni, akkor ez a menüpont is jól használható és a párbeszédablak felépítése is sokkal egyszerűbb, kevesebb dolgot kell beállítani. Viszont az eredmény is ennek megfelelően egyszerűbb lesz, vagyis csak két tényezőt tudunk egyszerre vizsgálni és például ezek interakcióit sem fogja belevenni a vizsgálatba a szoftver.

Én viszont most nem ezt szeretném bemutatni, hanem természetesen a bonyolultabb változatot. Ez azt jelenti, hogy amennyiben egy Two-way ANOVA elemzést szeretnék Minitab-ban elkészíteni, akkor a képen látható ’Fit General Linear Model…’ menüpontot kell az egérrel izgatni…

A már megszokott módon az izgatásra a program egy párbeszéd panel megjelenésével reagál. A bal oldalon megjelennek a vizsgálat tábla mezői. A jobb oldalon fent található egy ’Responses:’ jelzésű beviteli mező, ahol annak az oszlopnak a nevét kell megadni, amelyik a vizsgált jellemző adatait tartalmazza. Ide több mező nevét is meg lehet adni; azaz, ha nemcsak egy, hanem több kimeneti tényező is vizsgálható egyszerre. Viszont ezt még sohasem próbáltam ki, szóval a várható eredményekről nem tudok beszámolni. Viszont esetünkben nincs is erre szükség, hiszen egyetlen jellemzőnk van: az, hogy milyen mélyen hatol be a nyílvessző a zselatinba. A ’Responses’ mező alatt található a ’Factors’ mező, ahová pedig be tudjuk adni a két tényezőt, amelyekről feltételezzük, hogy befolyásolják a mélységet. A harmadik mező felirata ’Covariates’, amelyet most nem fogunk használni, de érdemes tudni, hogy mi is ez. A ’Covariates’-ek nem kategória jellemzők, hanem folytonos változók, amelyek segítségével pontosabbá lehet tenni a modell becslését. Tegyük fel, hogy a zselatin hőmérséklete befolyásolná a nyílvessző befúródásának a mélységét a zselatinba. Ha mérnénk a zselatin hőmérsékletét, és minden lövéshez odaírnánk, hogy a lövés pillanatában mekkora volt a zselatin hőmérséklete, akkor a hőmérséklet egy „Covariate” lenne és ezt a mezőt a ’Covariates’ mezőbe vennénk fel.

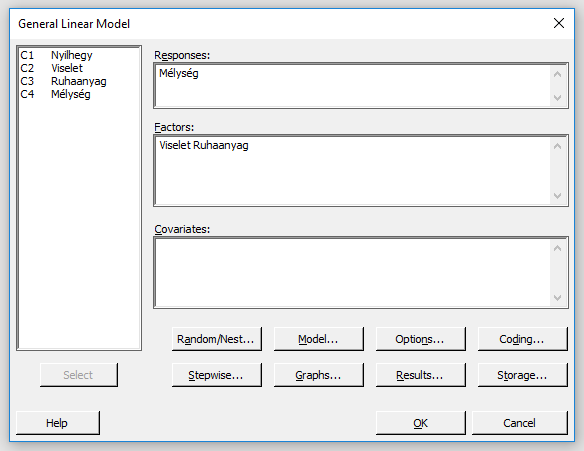
A párbeszéd panel alján ismét egy rakat különféle nyomógombot lehet látni, amelyek további párbeszéd paneleket fognak megjeleníteni. Az egyik legfontosabb a ’Model…’ feliratú gomb, amelynek hatására a következő ablak jelenik meg:

A bal felső sarokban megjelenik a faktorok és kovariánsok listája (’Factors and Covariates:’), ahonnan majd választani lehet. Jelen példánkban csak két faktor szerepel itt, vagyis nem sok mindent kell itt beállítanunk. Mivel érdekel minket a viselet és a ruhaanyag interakciója is, ezért ezt is fel szeretnénk venni a párbeszéd panel alján lévő széles mezőbe, amelyen a ’Terms in the model:’ felirat szerepel. A felvitel módja elsőre nem tűnik nyilvánvalónak, mert a panel jobb felső részén lévő ’Add’ gomb ki van szürkítve, azaz nem használható. Ennek igen prózai oka van: Egyszerűen ki kell jelölnünk azokat a faktorokat, amelyeknek az interakcióját fel akarjuk venni a ’Terms in the model’ listára.

Ebben a pillanatban az ’Add’ gomb használhatóvá válik és ha megnyomjuk, akkor a Viselet*Ruhaanyag interakció is megjelenik a lenti adatbeviteli mezőben.

Ebben a konkrét esetben ez nem tűnik fontosnak, de lehetne itt akár 4-5 faktor és 2-3 kovariáns is. Akkor viszont már igenis fontossá válik, hogy mely faktorok és kovariánsok együttes hatását szeretnénk megjeleníteni az ANOVA-táblában. A legfelső mező felirata ’Weights’. Ezt a mezőt csak akkor használjuk, ha az egyes megfigyelések szóródása nem egyenletes. Ilyenkor a szóródás mintázatának inverzét hozzá lehet adni súlyozásként a vizsgálathoz. A következő két mező már jól ismert, itt adható meg a teszt megbízhatósági szintje (’Confidence level’) és a megbízhatósági intervallum jellege (’Type of confidence interval’), azaz baloldali, jobboldali vagy kétoldali az intervallum. Az igazi érdekesség a negyedik beviteli mezőnél kezdődik, amelyet a ’Sum of Squares for tests:’ névvel illettek a szoftver alkotói. Itt kétféle számítási mód szerint lehet választani, a kiválasztott érték lehet ’Sequential (Type I), illetve Adjusted (Type III).

Legyen elég annyi, hogy a kétféle név kétféle számítási módot takar. A ’Sequential (Type I)’ esetében a szoftver az egyes tényezőket a modellben megadott sorrendben veszi figyelembe; azaz, ha először jön a Viselet és aztán a Ruhaanyag, akkor a Viselet lesz először kiértékelve és a Ruhaanyag csak azután és csak a végén jön a két tényező interakciója. Ezt inkább ’balanced’ design esetén érdemes választani (lásd fentebb), nem kiegyensúlyozott adatok esetén a tényezők különböző sorrendje különböző eredményeket hozhat.

Ha az ’Adjusted (Type III)’ lehetőséget választjuk, akkor viszont nem számít a tényezők sorrendje. Ezt viszont akkor érdemes inkább alkalmazni, ha azt várjuk, hogy a tényezők interakciója szignifikáns mértékű lesz. Akit ez a téma mélyebben érdekel, itt találhat további információkat aránylag emészthető formában (de persze angolul):

http://md.psych.bio.uni-goettingen.de/mv/unit/lm_cat/lm_cat_unbal_ss_explained.html

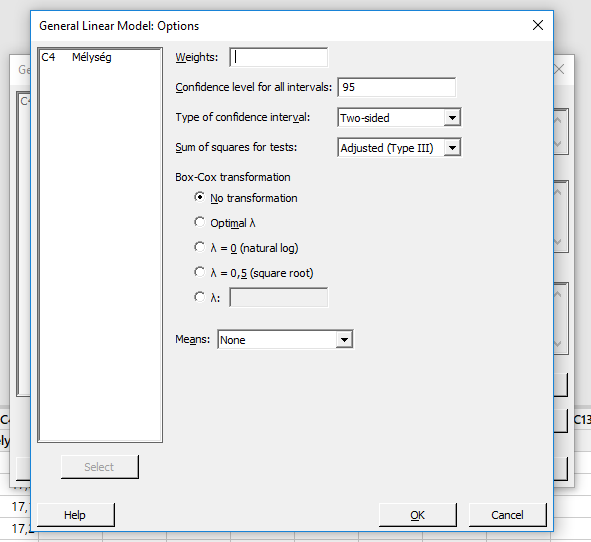
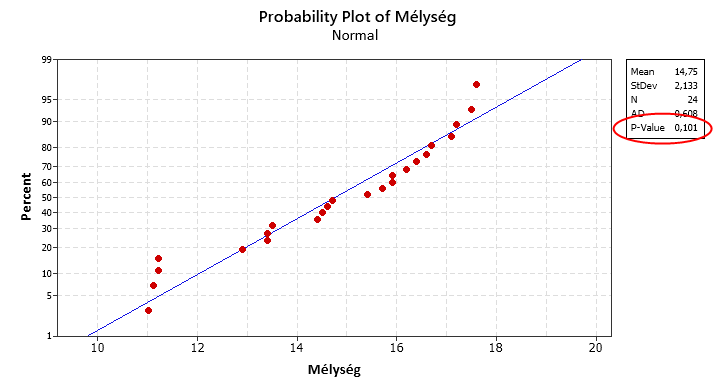
A párbeszéd panel utolsó része a ’Box-Cox transformation’, amelyet akkor alkalmazunk, ha az adataink nem normál eloszlásúak. Szerencsére ez esetben az adatok nagyjából normál eloszlásúak (illetve a lenti teszt nem igazolja, hogy az adatok NEM normál eloszlásúak – noha azért látható a diagramon néhány olyan pont, ami nem igazán illeszkedik a képbe), így ezt a beállítást nem szükséges piszkálni. Ha viszont az adatok eloszlása nagyon eltér a normál eloszlástól, akkor megfontolandó valamilyen adattranszformáció.

Akkor végre elérkeztünk az eredményekig. Az első párbeszédpanelen az ’OK’ gombra kattintva egy hosszú jelentést kapunk. Először a faktor információk jelennek meg, ez csak egy összefoglaló arról, hogy milyen tényezőket használtunk fel a vizsgálathoz. Ez később jöhet jól, ha utólag kell beazonosítanunk a vizsgálatot. A cím után látható titokzatos ’Method’ feliratú rész igazából egy kicsit nehezen értelmezhető és inkább technikai jellegű információ, valószínűleg ezért is nem adtak a fejlesztők egy kicsit beszédesebb nevet ennek a pontnak. A tesztünk eredménye szempontjából nem ad extra információt. A ’Factor information’ nevezetű táblázat viszont csak annyit tartalmaz, hogy milyen tényezőket vizsgáltunk és ezek milyen kategóriákat tartalmaznak, vagyis összefoglalja az adathalmazunk csoportosítási szempontjait.

Ezután jelenik meg az ANOVA-táblázat. A különbség a korábban táblázatkezelővel készített verzióhoz képest csak annyi, hogy a végén nem az F-eloszlás kritikus értékei szerepelnek, hanem a vonatkozó P-értékek. Mivel mindhárom P-érték 0, ezért a következtetésünk az, hogy mind a Viselet, a Ruhaanyag típusa és a két tényező interakciója is szignifikánsan befolyásolja a végeredményeket. Ha a P-értékek közül bármelyik nagyobb lenne, mint az általunk választott megbízhatósági szint, akkor annál a tényezőnél nem tudnánk kizárni a lehetőségét, hogy a tényező értékét csak a véletlen befolyásolja.

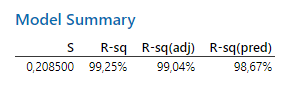
Ezután következik a ’Model Summary’, azaz az R-sq (R-squared) értékek, amelyek a regresszióelemzéshez hasonlóan itt is azt reprezentálják, hogy a modell mennyire fedi a valós értékek szórását. Mivel mindhárom R-sq érték 98% feletti értéket vett fel, ez azt jelzi, hogy a fent kiszámított modell nagyon nagy mértékben magyarázza az eredmények alakulását, vagyis a kapott mérési eredményeket a kísérlet során tényleg csak a ruhaanyag, a viselet módja és ezek interakciója befolyásolta, más tényező nem.

Végül a faktorok összes kombinációjának listája következik. Ez a táblázat már a regresszióelemzéshez tartozik (Tudom, hogy gőzgép, de mi hajtja? – Egyváltozós lineáris regresszió – a regressziós egyenes meghatározása) mert ez is része a General Linear Model-nek, amelynek a segítségével elvégeztük a kéttényezős varianciaanalízist. A táblázat bal szélső oszlopában van felsorolva az összes tényező összes lehetséges kombinációja. A második oszlop tartalmazza az adott kombinációjához tartozó regressziós tényezőt. A harmadik oszlop a titokzatos ’SE Coef’ nevet viseli, ez a regressziós tényező standard hibája. Ez logikusan minél kisebb, annál megbízhatóbb a regressziós tényező becslése. Ez igényel egy kis magyarázatot. Ha a vizsgált sokaságból újra és újra mintát vennénk, a regressziós együttható nem mindig lenne ugyanaz, tehát egy megadott tartományban mozogna. Ezt a tartományt adja meg az ’Se Coef’ értéke.

A ’T-Value’ tulajdonképpen a regressziós tényező és a standard hiba hányadosa, azaz ’Coef’/’SE Coef’. Ez a T-érték segít eldönteni, hogy a T-teszt értékét, a ’P-Value’ oszlop pedig a teszt P-értékét adja meg. Természetesen a P-értéket teljesen ugyanúgy határozza meg a program, mint ahogyan azt korábban már ismertettem, azaz a kapott T-értéket összehasonlítja az adott jellemzőhöz tartozó kritikus T-értékhez. Ha a P-érték kisebb, mint a választott megbízhatósági szint, az azt jelzi, hogy az adott faktor szignifikánsan módosítja a kimeneti jellemzőt.

Ebben a táblázatban egy kicsit furcsa eredmény született, mert két olyan kombináció van a listában, ahol a P-érték nagyobb, mint 0,05. Ez a Laza Farmer65%Pamut és a Laza Farmer95%Pamut, azaz nagyjából azt lehet kiszűrni, hogy az mindegy, ha egy 95% pamut tartalmú farmert lazán vagy szorosan viselünk, egyforma mélységben fog belénk mélyedni a nyílvessző. Viszont ez nem áll meg; mert, ha grafikusan ábrázolom az eredményeket, akkor jól látszik, hogy van különbség a kétféle viselet között.

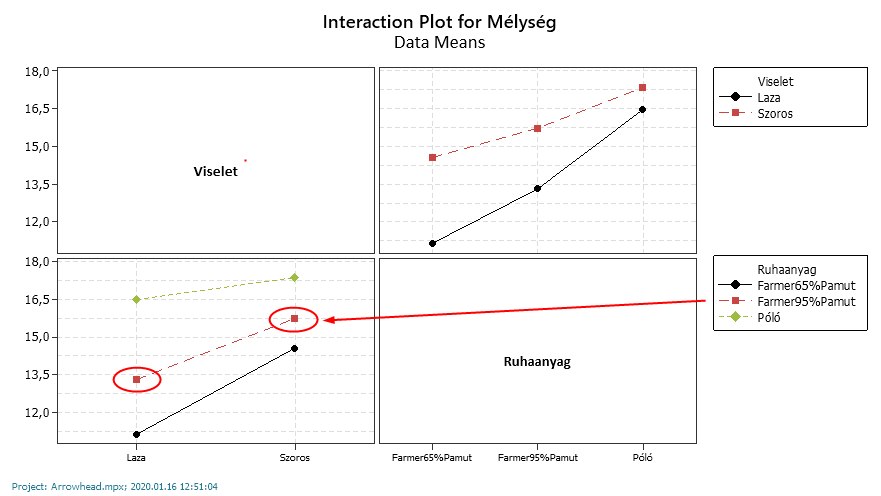
És szégyen – nem szégyen rájöttem, hogy még egy dologgal foglalkozni kell és ez a kombinációk kiértékelési módja. Itt többféle stratégia közül tudunk választani. Sajnos fennáll a veszélye, hogy a kiértékelés módjától függően különböző eredményeket fogunk kapni. A következő lehetőségek közül tudunk választani:

• None – Ilyenkor nincs speciális kiértékelési stratégia, a program a modell szerinti összes lehetőséget ki fogja értékelni
• Stepwise – Ez a stratégia egy üres modellből indul ki, ezután a program minden egyes lépésben hozzáad egy kombinációt a modellhez a modell létrehozásakor megadott sorrend szerint. A program addig adja hozzá sorban a kombinációkat a listához, amíg a modellben nem szereplő összes tényező P-értéke nagyobb nem lesz, mint a megadott megbízhatósági szint.
• Forward Selection – Ez a stratégia is egy üres modellből indul ki. Ezután a program először a legerősebb hatású (leginkább szignifikáns) kombinációt adja hozzá a modellhez, majd sorban az egyre kevésbé releváns kombinációkat. A program addig adja hozzá sorban a kombinációkat a listához, amíg a modellben nem szereplő összes tényező P-értéke nagyobb nem lesz, mint a megadott megbízhatósági szint.
• Backward Elimination – Ez a stratégia úgy indul, hogy az összes kombinációt tartalmazza, majd egyenként kiveszi a legkevésbé szignifikáns kombinációkat. A program addig folytatja ezt, amíg a modellben nem szereplő összes tényező P-értéke nagyobb nem lesz, mint a megadott megbízhatósági szint.

Ezt a beállítást ’Stepwise…’ gomb megnyomásával érhetjük el.

Jelen esetben a ’Stepwise’ stratégia van kiválasztva. A lehetséges tényezők a ’Potential terms:’ alatti beviteli mezőben vannak felsorolva. Ez alatt van két gomb. Az ’E = Include term in every model’ segítségével el tudod érni, hogy a kijelölt tényező biztosan benne maradjon a végső modellben. Az ’I = Include term in the initial model’ segítségével meg tudsz jelölni egy olyan tényezőt, amelynél azt szeretnéd, hogy már a kezdő modellben benne legyen, azaz a stratégia ne üres modellel, hanem azokkal a tényezőkkel induljon el, amelyeket ezzel a gombbal megjelöltél.

Ezalatt van két adatbeviteli mező. Az ’Alpha to enter’ és az Alpha to remove’ mezőkben meg lehet adni, hogy mi az a küszöbérték, amely alatt hozzáadunk egy tényezőt a modellhez, vagy amely felett eltávolítjuk a tényezőt a modellből.

A soron következő gomb felirata ’Hierarchy…’. Ez nagyjából annyit jelent, hogy amennyiben hierarchikus modellt használunk, úgy a program azért figyelembe veszi a tényezők hierarchiáját, azaz először a fő tényezőket értékeli ki, ezután jönnek a különféle interakciók. Jelen példánkban ez nem releváns, de ha lenne 3, 4 vagy még több különféle kategória változónk, mint tényező, akkor már számíthat, hogy a kétszeres, háromszoros vagy akár négyszeres interakciókat milyen sorrendben vesszük figyelembe. Ne felejtsük el, hogy noha csak egy egyszerű kéttényezős varianciaanalízist akartunk elvégezni, tulajdonképpen egy General Linear Model-t készítünk, ami az eredeti célnál sokkal többet jelent.

Szóval maradtam a ’Stepwise’ stratégia mellett, és így a regressziós együtthatók táblázata egy kicsit más lett (Az ANOVA-táblázat emiatt nem változik meg):

Ebből a táblázatból már jobban kiderül, hogy a két fő tényező, a Viselet és a Ruhaanyag befolyásolják erősen a lövés mélységét, de a Laza farmer anyag is meghatározó. A többi tényező igazából nem játszik fontosabb szerepet abban, hogy milyen mélyen fúródik bele a nyílvessző a zselatinba.

A táblázat legutolsó oszlopával még nem foglalkoztunk, ez a ’VIF’ nevezetű oszlop. A ’VIF’ a ’Variance Inflation Factor’ nevű titokzatos elnevezés rövidítése. Igazából nem tudom, hogy hogyan is fordítanám le ezt a kifejezést, de igazából arra szolgál, hogy jelezze, ha esetleg több olyan tényező is lenne a modellünkben, amelyek egyébként korrelációban vannak egymással. Ezt a jelenséget az ismét csak nagyon titokzatosan hangzó ’multicollinearity’ (kimondani és leírni is nehéz) névvel illetjük. Ezt leginkább úgy tudnám leírni, mint amikor egy rockzenekarban a gitárosok egyszerre játszanak. Ha két gitáros játszik egyszerre, akkor még aránylag jól követhető, hogy melyik gitáros melyik dallamot játssza, de ha már három gitáros játszik egyszerre, akkor már nehéz megállapítani, hogy melyik gitáros játszik a legjobban. Ez majd lehet, hogy egyszer még részletesebben kitárgyalom majd, de most annyiban hagynám a történetet, hogy ha egy tényező esetében a VIF értéke nagyobb, mint 5, akkor élnünk kell a gyanúperrel, hogy a fent említett ’multi…izé’ esete forog fenn…

Ezután még megtekinthetjük a regressziós egyenes egyenletének becslését, szerintem ennek az alkalmazása biztosan izgalmas lehet.

Megjelenik még egy táblázat, ez tartalmaz egy szokatlan adatpontot (unusual observation), az adatsort megvizsgálva is látszik, hogy a 23 sorban lévő 12,9 jelentősen eltér a másik három adattól, kieső értéknek tekinthető, így vizsgálni kell, hogy mi az oka a jelentősebb eltérésnek.

A legutolsó elemzés a maradékok vizsgálata.

A maradékok elemzésekor kisebb egyenetlenségek látszanak az adatokon, például a bal felső diagramon a pontok nem teljesen egyenletesen helyezkednek el az egyenes körül, de a normál eloszlást jelző P-érték alapján nem tudjuk kizárni, hogy normál eloszlású az adatpontok halmaza. A bal felső ábrán a bal szélső ponthalmaz szóródása lényegesen kisebb, mint a többi csoporté. A jobb alsó diagramon a pontok szóródása középen kisebb, mint a két szélén.

Összefoglaló: A teszt sikerült, ki tudtuk mutatni, hogy a vizsgált tényezőknek jelentős hatása van a kilőtt nyílvessző befúródási mélységére, sőt még ennél is többet tettünk, hiszen leellenőriztük a modellünk jóságát. Meghatároztuk a modell viselkedését befolyásoló tényezőket, valamint megadtuk a regressziós egyenes becslését és vizsgáltuk a modell jóságát is. Talán egy kicsit még többet is tettünk, mint ami feltétlenül szükséges, egy kicsit olyan érzésem támadt, hogy a kevesebb több!