 Az egytényezős varianciaanalízis esetében sikerült tisztázni, hogy az tulajdonképpen egy kiterjesztett t-próba, azaz nem kettő, hanem három, négy vagy még annál is több adatsor átlagait hasonlítjuk össze (Emeljük új szintre a t-próbát - az egytényezős varianciaanalízis (One-way ANOVA)). Ez igaz is, de az egytényezős varianciaanalízis a három, négy vagy több adatsort egy megadott tényező szerint csoportosítja, például a sörhab mérési példa esetében (Egy kis sörhabológia – Példa egytényezős varianciaanalízisre (One-way ANOVA)) három különböző rekeszből kivett mintát hasonlítottunk össze. De ugyanígy össze lehet hasonlítani
Az egytényezős varianciaanalízis esetében sikerült tisztázni, hogy az tulajdonképpen egy kiterjesztett t-próba, azaz nem kettő, hanem három, négy vagy még annál is több adatsor átlagait hasonlítjuk össze (Emeljük új szintre a t-próbát - az egytényezős varianciaanalízis (One-way ANOVA)). Ez igaz is, de az egytényezős varianciaanalízis a három, négy vagy több adatsort egy megadott tényező szerint csoportosítja, például a sörhab mérési példa esetében (Egy kis sörhabológia – Példa egytényezős varianciaanalízisre (One-way ANOVA)) három különböző rekeszből kivett mintát hasonlítottunk össze. De ugyanígy össze lehet hasonlítani
- többféle műtrágya hatását az adott földterületen elérhető terméshozamra,
- többféle hajnövesztő hatását a haj növekedésére, vagy akár
- az oroszlánfókák bőgésének a hosszát Ausztrália különböző területein.
Rendben, de mi történik akkor, ha egy valamilyen számszerűsíthető értéket nem egy, hanem mondjuk két különböző tényező különféle kategóriáinak hatását szeretnénk felmérni?
Mire gondolok?
Például, hogy
- az adott földterületen elérhető terméshozamot nemcsak az alkalmazott műtrágya típusa, hanem az öntözéshez használt víz mennyisége is meghatározza, vagy
- a haj növekedését nemcsak a hajnövesztő szer típusa, de az alkalmazott kezelés módja is meghatározza, illetve
- az oroszlánfókák bőgésének hosszát nemcsak az határozza meg, hogy melyik területen élnek, hanem az is, hogy milyen ott az időjárás.
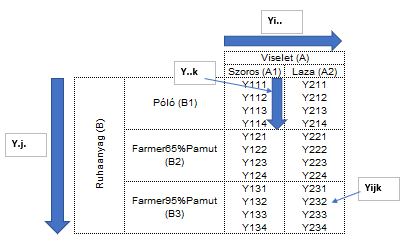
Szóval a végeredmények hatását nemcsak egy, hanem kétféle egymástól független – vagy nem független – tényező hatása határozza meg, és mindkét tényezőnek lehet két, három, négy vagy akár több különféle lehetséges értéke (kategória) is. A kéttényezős varianciaanalízis során a két tényező összes lehetséges kategóriájának összes kombinációját ki akarjuk próbálni a kísérlet során, és minden lehetséges kombinációhoz több mérési eredményt szeretnénk kapni, hogy ezekből is kapjunk egy átlagot. A kezdő táblázatunk valahogy így nézne ki:

A táblázat egyes oszlopai tartalmazzák az egyik tényező kategóriáit (A1, A2, …, Ai), a táblázat sorai pedig a másik tényező kategóriáit (B1, B2, …, Bj) tartalmazzák. A táblázat minden egyes mezőjében pedig megjelenik k darab eredmény (Y111 - Yijk).
Az izgalom fenntartása érdekében ismét megpróbáltam egy kicsit érdekesebb adatsort választani. Ebben az esetben egy olyan kísérlet eredményeit fogjuk kiértékelni, amelynek célja az volt, hogy megvizsgálja, a különféle nyílhegy típusok milyen mélyen hatolnak be az emberi testbe, ha azt különféle szövetből készült ruhák takarják. Azonban az sem mindegy, hogy a különféle szövetekből készült ruhákat az áldozat hogyan viseli, ezért azt is vizsgálták, hogy a ruhadarabok szorosan fedik az eltalált testfelületet, vagy csak lazán csüngenek felette.
Mielőtt valaki megijedne, a kutatók természetesen nem emberekkel kísérleteztek, hanem a különféle szövetekkel befedett zselatin tömbökbe lőtték bele a nyílvesszőket, majd megmérték a találatok mélységét. Az értekezésben az adatok a következő formában voltak közölve:

A tömörség kedvéért én csak azt akarom elemezni, hogy a nyílvesszők milyen mélyen fúródtak bele a zselatin tömbökbe (Penetration (cm)), illetve csak egyféle nyílhegy adatait fogom megvizsgálni, ezért az adatokat átrendeztem a következő módon (már csak, hogy ismerős legyen a fentebbi ábrából):
Eddig jó, de mi is lesz a vizsgálatunk célja? Mi lesz a nullhipotézis? Azt szeretnénk tudni, hogy vajon az így elkészített adathalmaz adatainak szóródását az egyes tényezők hatása okozza, vagy a csoportokon belüli szóródás a meghatározó. Ha a csoportok közötti szóródás hatása erősebb, mint a csoportokon belüli szóródásoké, akkor a vizsgált tényezők befolyásolják a vizsgált jelenség eredményét. Amennyiben viszont a csoportokon belüli szóródások az erősebbek, akkor azt mondhatjuk, hogy a vizsgált tényezők hatása a vizsgált jelenségre nem jelentős.
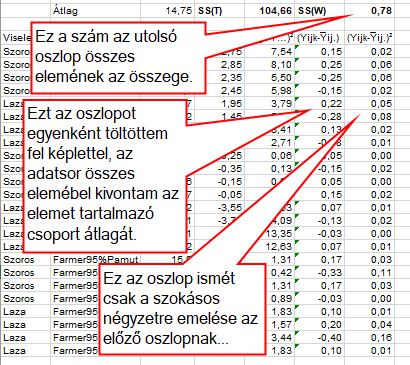
Fontos, hogy mit jelentenek az egyes képletekben található kifejezések, ezért a fenti képen azt is megpróbáltam bemutatni, hogy az i, j és k betűk mit jelölnek tulajdonképpen. Kezdjük az elején. Az Yijk kifejezés a fenti táblázat i-dik oszlopának és j-dik sorában található adathalmaz k-dik elemét jelöli. Összesen ezek szerint i*j*k darab adatunk van összesen.
Az Y̅ij. kifejezés a táblázat egyes mezőiben található adatsorok átlagait jelöli a lentebb látható módon

Az Y̅i.. és az Y̅.j. kifejezések a tényezőkhöz tartozó összes adat átlagait jelölik, tehát az Y̅i.. a Viselet tényezőhöz Szoros (A1) és a Laza (A2) kategóriák minden elemét jelentik, az Y̅.j. pedig a Ruhaanyag tényező Póló, Farmer65%pamut és Farmer95%pamut kategóriáihoz tartozó összes adat átlagait.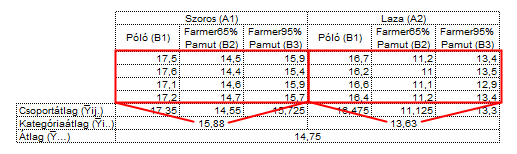
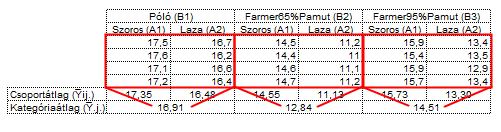 Végül az adathalmaz összes elemének átlagát az Y̅… kifejezéssel jelöltem.
Végül az adathalmaz összes elemének átlagát az Y̅… kifejezéssel jelöltem.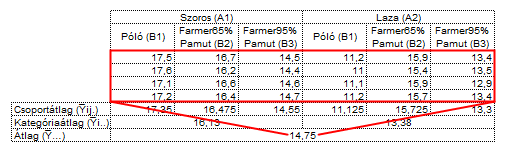
Nem túl jól olvasható jelölésmód, de talán egy kicsit logikusabb, mint ha minden átlagot külön betűkkel jelöltem volna. Így követni lehet, hogy az egyes adatok honnan származnak. A következő levezetés talán egy kicsit kuszának fog tűnni, de a cél az volt, hogy táblázatkezelőre legyen optimalizálva a számolás, vagyis, hogy minél áttekinthetőbb és minél gyorsabb legyen. Emiatt először nem is a fentebb berendezett módon kezdek el számolni, hanem alulról kezdem majd el a ’Sum of Squares’ kiszámítását.
Először kezdjük el az Y̅… kiszámításával, mert ez a legegyszerűbb. Ez esetben az adatokat sorba rendezem egy szekvenciális táblázatba, majd kiszámolom mind a 24 adat átlagát. Ezt persze a fenti táblázat segítségével is könnyedén megtehetjük, de a következő lépés már nehezebb lenne a korábbi formátum alkalmazásával.
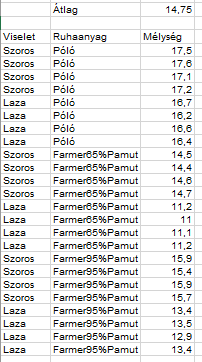
Ok, de mi nem erre az átlagra vagyunk kíváncsiak, hanem arra, hogy az egyes adatpontok egyenként milyen távolságra vannak az előbb kiszámított átlagtól. Az (Yijk-Y̅…) oszlopot úgy kaptam meg, hogy minden egyes adatpontból kivontam a fenti Nagyátlagot, így megkapom az egyes pontok átlagos eltérését az átlagtól.
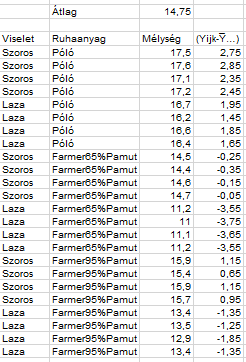
Ezután ezeket a távolságokat egyenként négyzetre emeltem:
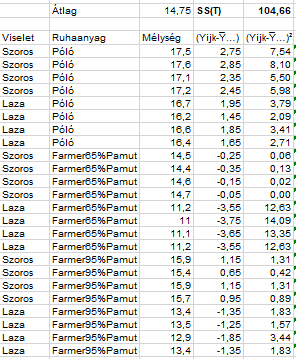
Ha az utolsó oszlop összes adatát összeadom, akkor megkapom a teljes ’Sum of Squares’-t, azaz az SS(T)-t, amely ez esetben 104,66-tal egyenlő. Ez az adathalmaz adatainak teljes szóródása, amelyet tulajdonképpen meg szeretnénk magyarázni. Ebben fognak segíteni majd a különféle csoportosításokkal végzett számítások. A következő lépésben a csoportokon belüli ’Sum of Squares’ értékek kiszámítását fogjuk elvégezni, ezt fogjuk majd hasonlítani a különféle tényezők és kategóriák által okozott szóródásokhoz.
Nos, ez már nem lesz ennyire egyszerű, bár nem is lesz nagyon bonyolult. A fenti függőleges táblázatot fogjuk folytatni, de szükségünk lesz az egyes csoportok átlagaira, mert a csoportok elemeiből az elemet tartalmazó csoport átlagát fogjuk kivonni, ezt viszont oda kell csalni valahogy. Az egyszerűség kedvéért én most kézzel végig írtam ezt az oszlopot, mert csak 24 cella értékét kellett kiszámítani. A csoportátlagokat egy másik táblázatban a fentebb tárgyalt módon határoztam meg. Nagyobb adatmennyiség esetében valószínűleg elkezdtem volna képletekkel trükközni, de most ezt láttam gyorsabbnak.
Így megkaptam a ’Sum of Squares’ within, avagy az SS(W) értékét.
Már csak az egyes tényezőkhöz tartozó ’Sum of Squares’ értékeket kell megadni. A fent ismertetett formában kialakított táblázatok alkalmazásával ez sem lesz nehéz. Az A-tényező, azaz a Viselet SS-ét a következő módon kapjuk meg:
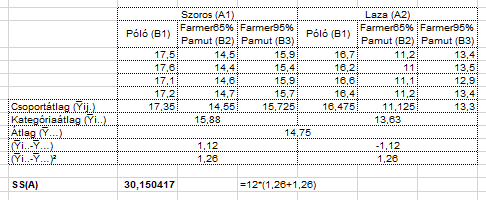
Itt a tényezőátlagokat (Y̅i..) és a Nagyátlagot (Y̅…) vonjuk ki egymásból, majd ezeket a különbségeket emeljük négyzetre. A ’Sum of Squares’ értékét úgy kapjuk meg ez esetben, hogy az így kapott négyzetösszeget megszorozzuk az adott tényező adott kategóriájához tartozó adatok számával, azaz ez esetben 12-vel, így kijön SS(A) értéke. A B tényezővel elvégezük ugyanezt az ujjgyakorlatot, csak a másik módon berendezett táblázattal. Így megkapjuk az SS(B)-t is.

Ez nagyon jó, most már majdnem minden SS megvan ahhoz, hogy kitöltsük az ANOVA-táblázatot.
Kezdjük el a szabadsági fokok számával. A Viselet és a Ruhaanyag tényezők szabadsági foka (i-1), illetve (j-1), azaz 1 és 2 lesz. Mivel két tényezőnk van és nem zárható ki, hogy ezek együttes hatása más lesz, mint külön-külön, ezért a két tényező interakcióját is meg kell vizsgálnunk, ennek szabadsági foka pedig természetesen (i-1)*(j-1) lesz. Az Összes sor szabadsági foka a vizsgálatban részt vevő összes elem, azaz (i*j*k)-1, azaz 23 lesz. Így már csak a csoportokon belüli szórások szabadsági foka hiányzik, ezt pedig úgy kapjuk meg, hogy a 23-ból kivonjuk az összes többit, így 23-5=18-at kapunk:

Az előzőleg kiszámolt SS értékek alapján már könnyedén ki tudjuk tölteni a táblázat harmadik oszlopát:
Na igen, de a két tényező interakciójának SS értékét nem adtuk meg! Na itt elkezdett zavarossá válni a helyzet, mert többféle számítási módot is találtam erre a tényezőre. Az egyszerűség kedvéért én a Minitab blog útmutatását követtem – részben azért, mert ez volt a legegyszerűbb, illetve mert így össze tudom hasonlítani a kapott eredményt a Minitab eredményeivel – vagyis egyszerűen kivontam az SS(T)-ből az összes többi SS-t! Az egy kicsit érdekes megfontolás, hogy az a szóródás, ami sehova máshova sem passzol bele, az lesz az interakció, de egyelőre ezt ennyiben hagyom…
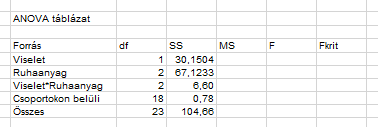
A többi igazából már gyerekjáték, mert a táblázatot innentől majdnem ugyanúgy kell kitölteni, mint az egytényezős ANOVA-táblát. Az MS oszlop mezőibe sorban a megfelelő SS/df hányadosok kerülnek (kivéve az utolsó sort!). Remélhetőleg még megvan az információ, hogy az MS
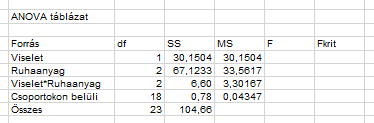
Az F-próbastatisztika megfelelő értékeit pedig úgy kapjuk meg, hogy a sor MS-értékét elosztjuk a Csoportokon belüli szóródás MS-értékével:
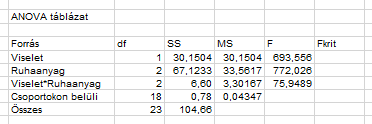
Jó magas F-értékeket kaptunk, ami arra utal, hogy a nullhipotézist nagy valószínűséggel el fogjuk utasítani. Ehhez viszont mégiscsak tudni kellene az Fkrit tényező értékét, mert ehhez fogjuk hasonlítani a megfelelő F próbastatisztikákat. Ezt viszont F-eloszlás táblázatból tudjuk kikeresni. Pechünkre a három F-értékhez két különböző Fkrit értéket kell kikeresni.
Mivel az F-eloszlások általánosságban két variancia hányadosai, ezért az éppen alkalmazandó eloszlás két dologtól függ, a két variancia – amelyeket elosztottunk egymással – szabadsági fokától. Az első sorban, azaz a Viselet esetében a Viselet szabadsági foka 1, a Csoportokon belüli szóródások szabadsági foka pedig 18, így az F-táblázatból is ennek megfelelően kell kikeresni a keresett határértéket:
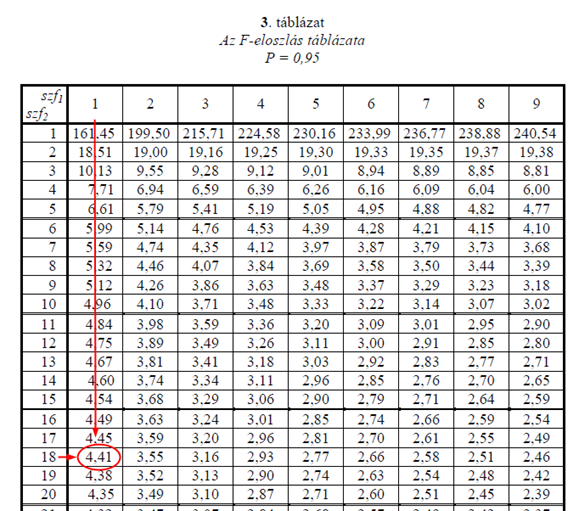
Mint látható, a határérték 4,41 lett. Ez jelentősen kisebb, mint a kapott F próbastatisztika (693,556). A második és a harmadik sorban a szabadsági fokok száma 2, így ezekhez is ki kell keresni a megfelelő határértéket:
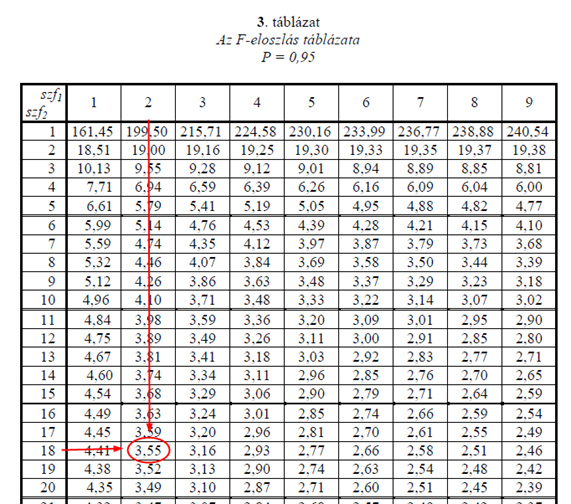
Ez 3,55, vagyis ez is sokkal kisebb, mint az adott sorokban kapott próba statisztikák. Vagyis az ANOVA-tábla ilyen lett:
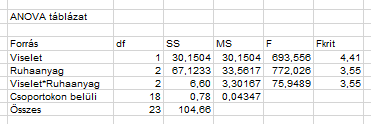
Mindhárom sorban magasabb lett a próba statisztika értéke a kritikus határértéknél, így azt mondhatjuk következtetésként, hogy a csoportok közötti variancia jelentősen nagyobb, mint a csoportokon belüli varianciák, így mind a Ruhaanyag típusa, mind a Viselet módja, illetve ezek együttes hatása is befolyásolja, hogy egy nyílvessző milyen mélyen fúródik bele a zselatinba. Előfordulhatott volna, hogy például a viselet módja nem határozza meg szignifikánsan a mélységet, de akkor azt az ANOVA-táblázat kimutatta volna.
Forrás:
Nichole MacPhee, Anne Savage, Nikolas Noton, Eilidh Beattie, Louise Milne, Joanna Fraser:A comparison of penetration and damage caused by different types of arrowheads on loose and tight fit clothing, Science & Justice, 21 November 2017
https://rke.abertay.ac.uk/en/publications/a-comparison-of-penetration-and-damage-caused-by-different-types-
Methods and formulas for Two-way ANOVA
https://support.minitab.com/en-us/minitab-express/1/help-and-how-to/modeling-statistics/anova/how-to/two-way-anova/methods-and-formulas/methods-and-formulas/





