
Mostanra eljutottunk oda, hogy rengeteg különféle statisztikai tesztet megismerhettünk, de van ezeknek egy olyan oldala, amelyről eddig így direktben még nem beszéltünk, ez pedig az, hogy vannak gyengébb és erősebb tesztek. Illetve inkább úgy fogalmaznék, hogy minden statisztikai tesztet végre lehet hajtani úgy, hogy gyenge és úgy is, hogy erős legyen. De mit is jelent az, hogy egy teszt „gyenge”, vagy „erős”?
Korábban már tisztáztuk a sokaság és a minta viszonyát, miszerint egy minta sohasem képezi le tökéletesen a sokaságot és sajnos ahányszor mintát veszünk a sokaságból, az annyiszor lesz mindig más és más (A nagy dobókocka kísérlet). Ez az apró bizonytalanság sajnos mindannyiszor felveti a kérdést, hogy a most kivett minta alapján elutasítottuk a nullhipotézist és elfogadtuk az ellenhipotézist. De mi történne akkor, ha vennénk egy újabb mintát ugyanabból a sokaságból? Vajon az újabb mintával elvégzett teszt ugyanazt az eredményt hozná vagy sem? De hagy menjek egy lépéssel még messzebbre. Vajon az első minta által elvégzett teszt eredménye egyáltalán megfelel a valóságnak? Ha ugyanezt a tesztet a teljes sokaságon végeznénk el (ha ez egyáltalán lehetséges), akkor vajon ugyanaz az eredmény jönne ki, mint a mintánkon elvégzett teszt alapján?
Úgy döntöttem, hogy az elméleti magyarázat helyett inkább egy gyakorlati példán keresztül mutatom be, hogy miért fontos a teszt ereje. Kivételesen nem keresgéltem érdekes történetet az adatokhoz, csak úgy egyszerűen készítettem két darab 20 elemű adatsort, amelyek csak egy kicsit különböznek egymástól. Éppen csak annyira, hogy megkülönböztethetők legyenek egymástól, de azért a különbség ne legyen teljesen nyilvánvaló. A két adatsor eloszlása körülbelül így néz ki:

Ha ezt a két „sokaságot” összehasonlítom egy egyszerű kétmintás t-próbával (Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba), akkor azt kapom eredményül, hogy a két adatsor statisztikailag különbözik egymástól. Ahogy az az alábbi elemzésből is látható, a két adatsor átlaga jelentősen eltér egymástól.

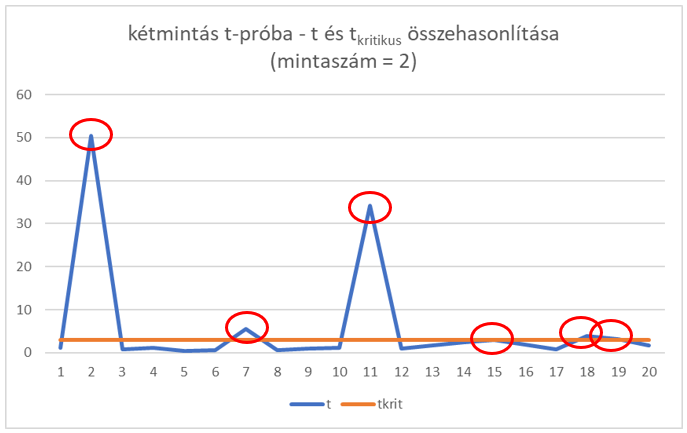
Ezek után a két sokaságból kivettem 20-20 különböző elemszámú mintát és azt vizsgáltam, hogy ha a mintákon is elvégzem ugyanezt a kétmintás t-próbát, akkor vajon ugyanazt az eredményt fogom-e kapni. Először kételemű mintákkal próbálkoztam, azaz véletlenszerűen kiválasztottam 2-2 darab mintát mindkét adatsorból, majd mindegyik mintapárral elvégeztem a fentebb említett kétmintás t-próbát. A részleteket nem osztom itt meg, de összefoglalva az jött ki, hogy a 20 mintapár esetén csak 6 esetben hozta ki a teszt ugyanazt az eredményt, mint a sokaságok esetében, 14 esetben az jött ki a minták vizsgálata alapján, hogy a két sokaság MEGEGYEZIK! Az alábbi diagramon a t próbastatisztika és a kritikus t-határérték látható. A diagramon jól látszik, hogy a tesztek túlnyomó részében a t-próbastatisztika értéke alatta van a kritikus t-határértéknek, ez pedig azt jelzi, hogy a nullhipotézist, hogy a két „sokaság” megegyezik, el kell, hogy fogadjuk annak ellenére, hogy ez esetben tudjuk, hogy a két sokaság különbözik, azaz a döntésünk hibás lenne.
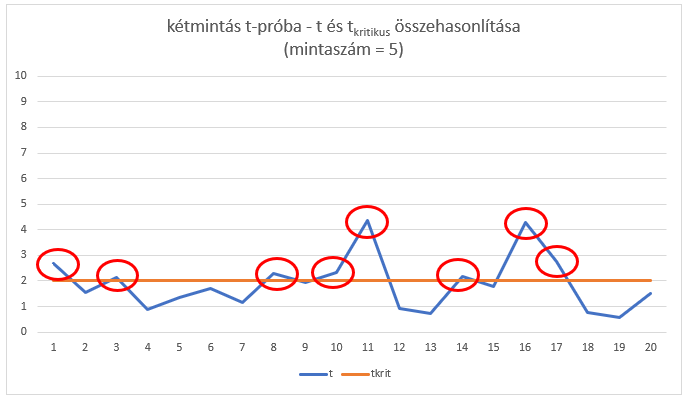
Ezután elvégeztem ugyanezt a gyakorlatsort, de ezúttal 5-elemű mintákat vettem ki a két sokaságból. Ebben az esetben már egy kicsivel jobb lett az arány, itt már 8 olyan eset volt, ahol helyesen döntött a teszt és „csak 12 olyan, ahol helytelen döntést hozott. Viszont az eseteknek még mindig több, mint a felében helytelen döntést hozott a teszt.
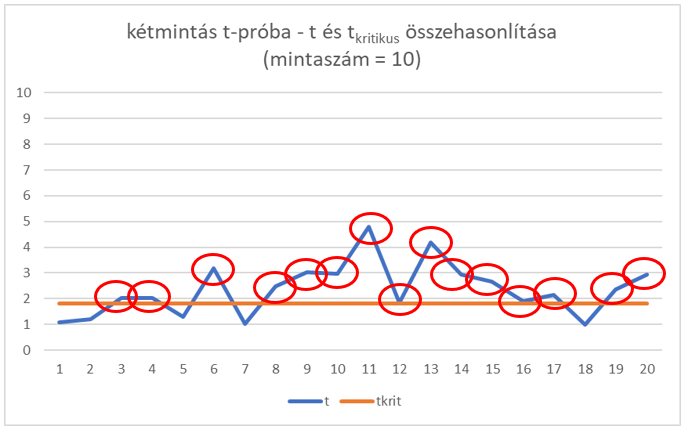
Ha mintaszámot 10-re emeltem, akkor még jobb lett az arány, de még mindig igen messze vagyunk a tökéletestől. Az ábrán talán egy kicsit nehezen látható, de a 20 esetből 15-ször már jól döntött a teszt:
Végül 20-elemű mintákkal próbálkoztam, itt már szinte minden esetben helyes döntést hozott a teszt. Ezen a diagramon már csak azt ez egy értéket karikáztam be, amelyik még mindig a kritikus t-vonal alatt van, mert ez a pont reprezentálja az egyetlen helytelen döntésünket.
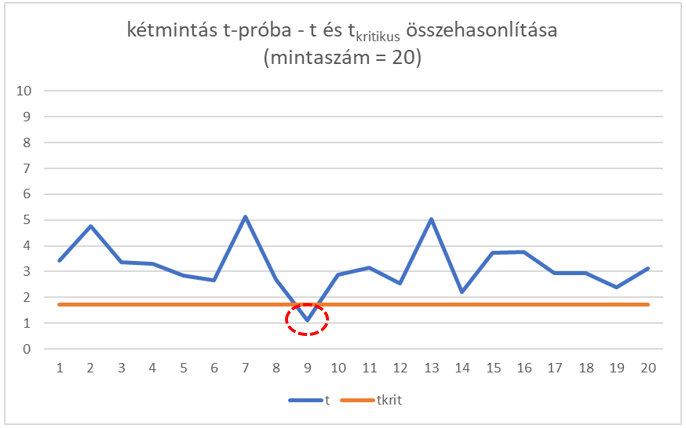
Az első tanulságunk ezek szerint az, hogy minél nagyobb mintát veszünk a sokaságból, annál megbízhatóbb lesz a döntésünk eredménye, annál kisebb az esélye a hibás döntésnek, azaz annál erősebb lesz a tesztünk.
Ez a következtetés egyből további jogos kérdéseket vet fel, úgymint ki tudjuk-e számolni, hogy mennyire erős a tesztünk, azaz mekkora a valószínűsége annak, hogy a mintánk alapján hibás döntést hozunk, illetve ki tudjuk-e számolni, hogy hány mintát kellene kivennünk a sokaságból ahhoz, hogy elfogadható biztonsággal azt tudjuk mondani, hogy helyesen döntöttünk. Az elfogadható biztonság itt természetesen nem 100%-ot jelent, mert a hiba valószínűsége – mint Damoklész kardja – mindig ott lebeg a fejünk felett, de mondjuk egy 95%-os vagy 99%-os biztonság már elfogadható lehet a számunkra. Nos, a válasz természetesen igen, bár minden teszthez más és más módszert és képleteket és számításokat kell alkalmazni. A példa kedvéért most nézzük meg, hogy a fenti példában hogyan alakulnak ezek az értékek. Először nézzük meg, hogy a 2, 5, 10 és 20 elemű minták esetében hogyan alakulna a teszt ereje:
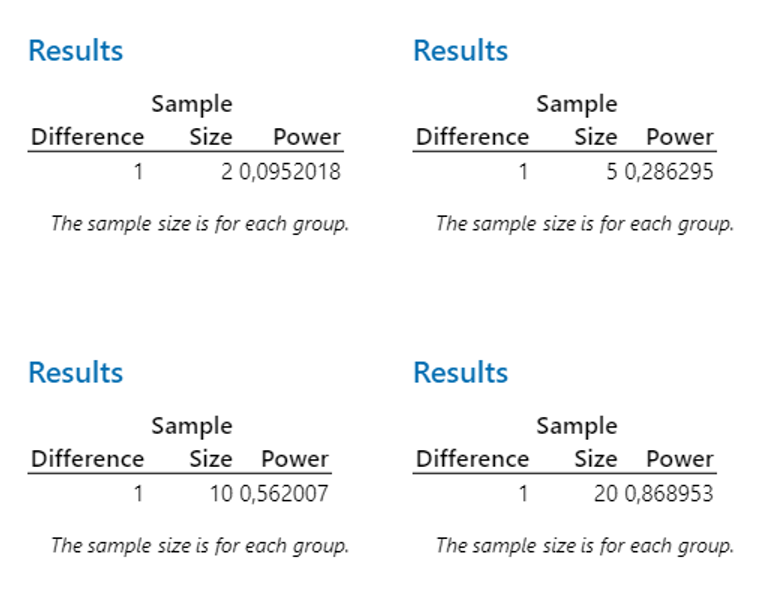
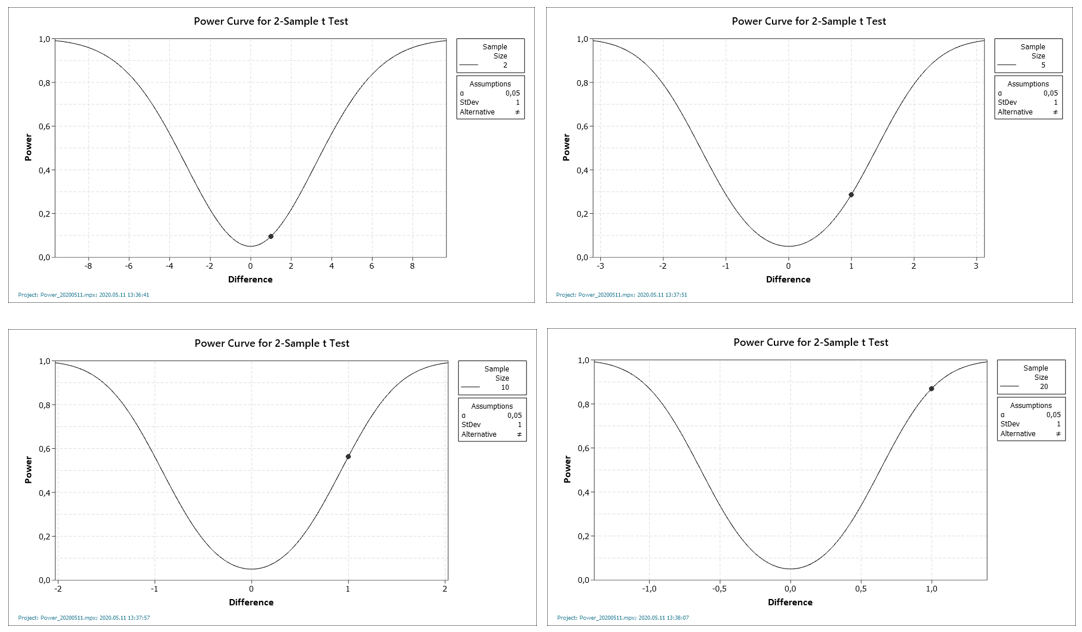
A számításokból jól látszik, hogy a mintaszám növekedésével hogyan javul a teszt megbízhatósága. Kételemű minták esetében még kevesebb, mint 10% a helyes döntés valószínűsége, ötelemű minták esetében ez már 29%, a tízelemű mintáknál már több, mint 56% ez a valószínűség. Érdekes, hogy a húszelemű minták alkalmazása esetén sem éri el a valószínűség a 90%-ot. A négy diagramon látható, hogyan mászik a fekete pont egyre feljebb a mintaszám növekedésével, de még a bal alsó diagramon is 0,9 alatt van a fekete pont a függőleges tengelyen. A jelenség okát a következő ábrák szemléletesen mutatják be:
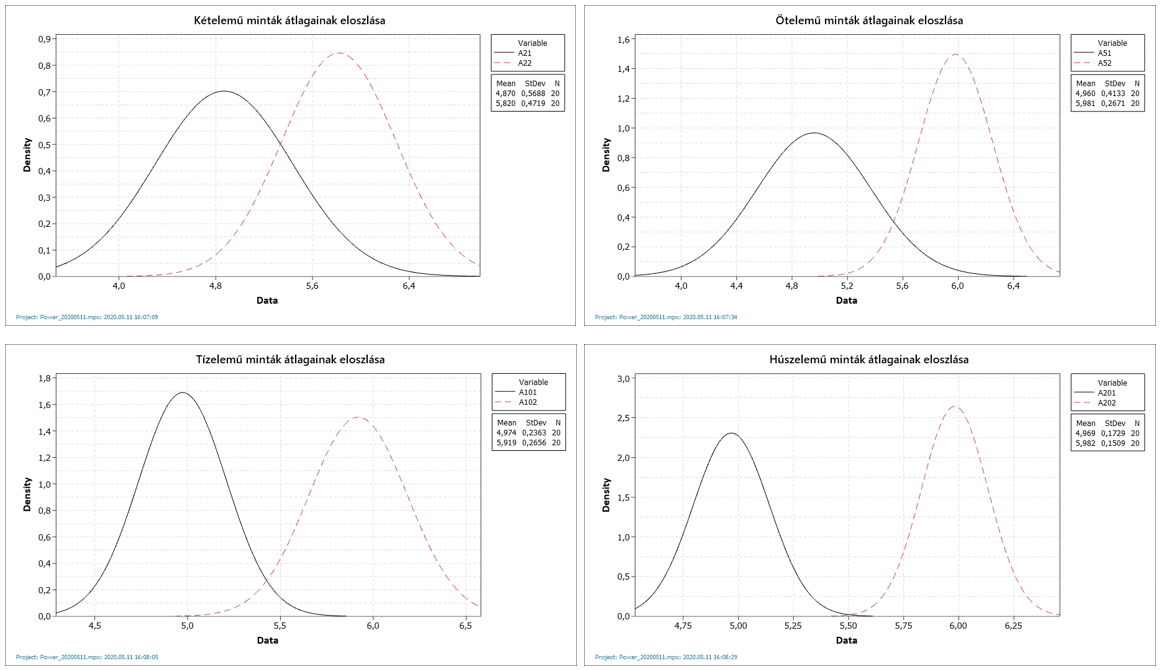
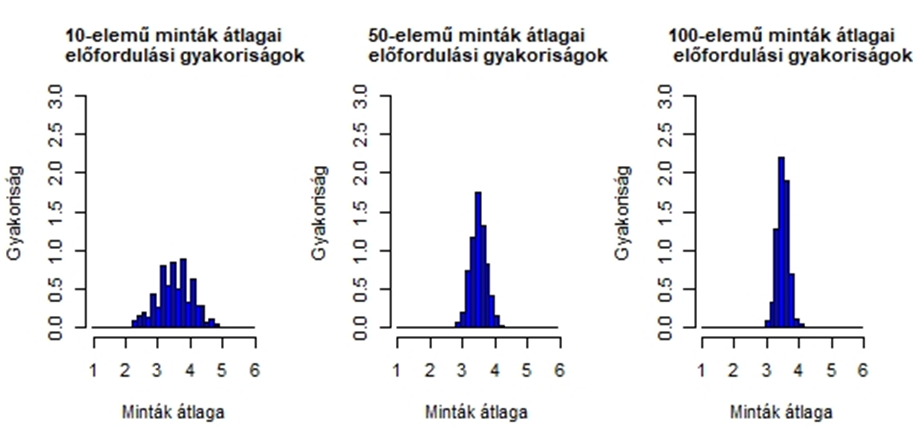
Az ábrákból érzékelhető, hogy a mintaszám növekedésével párhuzamosan egyre kevésbé fedik egymást a két sokaságból kivett minták átlagai. Ennek okait pedig egy korábbi írásomban már részletesen tárgyaltam (A nagy dobókocka kísérlet). Abban a cikkben egy gyakorlati példán keresztül mutattam be azt, hogyan csökken a mintaátlagok szórása a mintaszám növekedésével. Emlékeztetőül újra megmutatom azt az ábrát, amely ezt szemléletesen megmutatja.
Végezetül nézzük, meg, hogy hány mintát kellene vennünk a két sokaságból ahhoz, hogy 95%-os valószínűséggel biztosak tudjunk lenni abban, hogy a teszt helyes döntést fog hozni.
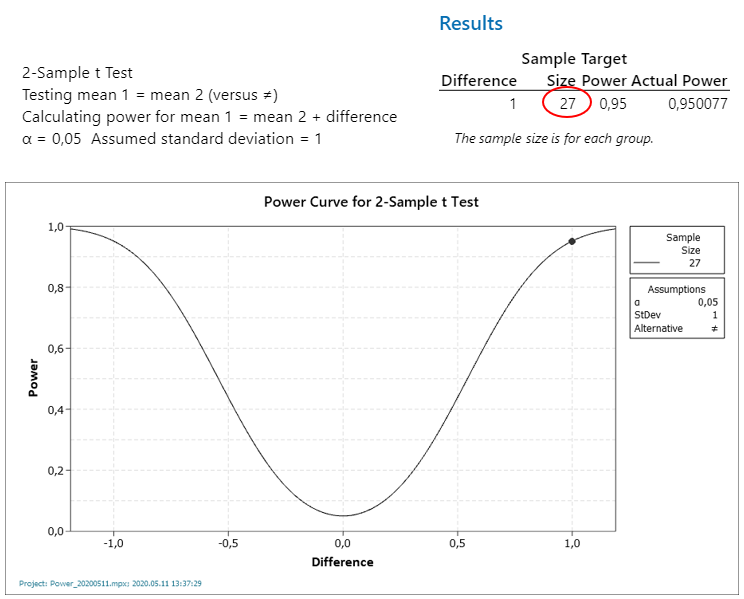
A történet rövid tanulsága az, hogy ezekben az egyszerű tesztekben sem szabad feltétel nélkül megbízni, mindig érdemes meggyőződni arról, hogy elegendő mennyiségű minta áll rendelkezésre ahhoz, hogy nagy valószínűséggel helyes döntést hozzunk.





